Оптимальним є префіксний код, для якого добуток L×F мінімальний: L×F® min

ТЕОРІЯ ІНФОРМАЦІЇ

Навчальний посібник

з дисципліни “Теорія інформації”

для студентів механіко-математичного факультету

всіх форм навчання

Усі цитати, цифровий та

фактичний матеріал,

бібліографічні

відомості перевірені,

запис одиниць

відповідає

стандартам

Укладач Н.О. Тулякова

Відповідальний за випуск О.П. Чекалов

Декан механіко-математичного

Факультету С.М. Верещака

Суми

Вид-во СумДУ

Міністерство освіти і науки України

Сумський державний університет

Тулякова Н.О.0

ТЕОРІЯ ІНФОРМАЦІЇ

Рекомендовано Міністерством освіти і науки України

як навчальний посібник для студентів вищих навчальних закладів

Суми

Вид-во СумДУ

УДК 004.02(075.8)

Т 82

Рекомендовано Міністерством освіти і науки України

(лист № 14/18 –Г - 965 від 06.05.2008 р.)

Рецензенти:

д-р фіз.-мат. наук, проф., член-кореспондент

НАН України В.Л. Макаров

(Київський національний авіаційний університет);

д-р техн. наук, проф. В.В. Лукін

(Харківський національний аерокосмічний

університет „ХАІ”);

д-р фіз.-мат. наук Д.О. Харченко

(Інститут прикладної фізики НАН України)

Тулякова Н. О.

Т 82 Теорія інформації: Навчальний посібник. - Суми: Вид-во СумДУ, 2008.- 212 с.

ISBN 978-966-657-199-4

У посібнику викладено курс „Теорії інформації”, що складається з трьох частин: основні положення теорії інформації, економне кодування (стиснення інформації) і завадостійке кодування. Теоретичний матеріал супроводжується великою кількістю прикладів розв'язання задач. До кожного з розділів підібрані задачі, наводяться відповіді до них. Наприкінці кожної частини курсу подаються контрольні запитання.

Навчальний посібник розрахований на студентів та аспірантів вищих навчальних закладів, може бути корисним викладачам і всім, хто займається питаннями вимірювання інформації і методами побудови кодів з метою стиснення і захисту від завад.

УДК 004.02(075.8)

ISBN 978 -966-657-199-4

Навчальне видання

Тулякова Наталія Олегівна

ТЕОРІЯ ІНФОРМАЦІЇ

Навчальний посібник

Дизайн обкладинки Р.С. Волкова

Редактори: Н.З.Козак, Т.Г. Чернишова

Комп’ютерне верстання Н.О. Тулякової

Підп. до друку 23.06.2008.

Формат 60х84/16. Папір офс. Гарнітура Times New Roman Cyr. Друк офс.

Ум. друк. арк. 12,32. Обл.-вид арк. 11,26.

Тираж 150 пр. Вид. № 282

Зам. №

Видавництво СумДУ при Сумському державному університеті

40007, Суми, вул. Римського-Корсакова,2

Свідоцтво про внесення суб'єкта видавничої справи до Державного реєстру

ДК № 3062 від 17.12.2007.

Надруковано у друкарні СумДУ

40007, Суми, вул. Римського-Корсакова, 2.

ПЕРЕДМОВА

У даному посібнику подано теоретичний матеріал, приклади розв'язання практичних завдань з навчальної дисципліни „ Теорія інформації ” для студентів спеціальності „ Інформатика ” напряму „ Прикладна математика ”.До кожного з розділів навчального курсу підібрані задачі, наводяться зразки їх розв'язання і відповіді до задач. Наприкінці кожного розділу подаються контрольні запитання для самоперевірки отриманих знань і вмінь.

Навчальний посібник складається з трьох частин. У першій частині розглянуто фундаментальні положення теорії інформації за Шенноном: способи вимірювання та передачі інформації, поняття кількості інформації та ентропії випадкових подій, основні властивості кількості інформації і ентропії, характеристики дискретного каналу зв ' язку. У другій частині подано основи економного кодування інформації, розглядаються статистичні та словникові алгоритми стиснення даних; класифікація і загальна характеристика систем стиснення інформації. Третя частина присвячена основним принципам та методам завадостійкого кодування інформації, наводяться загальні властивості завадостійких (коригувальних) кодів, принципи побудови і способи задання лінійних блокових кодів, що виправляють помилки, та основні типи цих кодів.

Опанування базових знань та набуття практичних навичок при вивченні курсу „ Теорія інформації ” створять засади для подальшого засвоєння спеціалізованих дисциплін у сфері інформатики, комп'ютерних систем, автоматики та керування, телекомунікацій і т. ін. і буде суттєвим підґрунтям для подальшого вдосконалення професійної майстерності спеціалістів у цих галузях.

Частина I Основи теорії інформації та кодування

Розділ 1 ОСНОВНІ ПОЛОЖЕННЯ ТЕОРІЇ ІНФОРМАЦІЇ

1.1 Предмет курсу. Види інформації. Теорема дискретизації

Теорія інформації - це розділ кібернетики, в якому за допомогою математичних методів вивчаються способи вимірювання інформації та методи її кодування з метою стиснення інформації і надійної передачі каналами зв'язку.

При формальному поданні знань кожному досліджуваному об'єкту ставиться у відповідність числовий код, зв'язки між об'єктами так само подаються кодами. Для переведення неформальних даних у формальний цифровий вигляд використовуються спеціальні таблиці кодування. Найпростіший приклад такої таблиці - ASCII (American Standard Code for Information Interchange), що зіставляє друкованим та керуючим символам числа від 0 до 127.

Інформація може бути двох видів: дискретна(цифрова) і неперервна(аналогова).

Неперервна інформація – це дані, що одержані при неперервному за часом процесі змінювання деякої випадкової величини і описуються неперервними (аналоговими) функціями.

Дискретна інформація – це цифрові дані, одержані у результаті квантування (дискретизації) неперервної величини за часом, рівнем або тим і іншим одночасно (рис.1.1). Дискретну інформацію зберігати і обробляти набагато простіше, оскільки вона являє собою послідовність чисел. У двійковій системі числення дискретна інформація являє собою послідовність 0 та 1.

За найменшу одиницю ємності цифрової інформації беруть біт (bit, binary digit) – одну позицію для двійкової цифри. Складені одиниці: 1 Кб = 2¹⁰= 1024 б; 1 Мб = 2²⁰≈ 10⁶ б; 1 Гб = 2³⁰≈ 10⁹ б; 1 Тб = 2⁴⁰≈ 10¹² б; 1 Пб = 2⁵⁰≈ 10¹⁵ б.

Для переведення неперервної інформації в дискретну і навпаки використовуються спеціальні пристрої модуляції/демодуляції - модеми. Швидкість передачі інформації вимірюється в кількості переданих за одну секунду бітів – бодах (baud): 1 бод = 1 біт/с (bps).

Пристрій, що реалізовує процес дискретизації неперервного сигналу, називається аналогово-цифровим перетворювачем (АЦП). Частота, з якою АЦП проводить виміри аналогового сигналу і видає його цифрові значення, називається частотою дискретизації. Пристрій, що інтерполює дискретний сигнал у неперервний називається цифро-аналоговим перетворювачем.

Чим вища частота дискретизації, тим точніше переведення неперервної інформації в дискретний сигнал. Проте із зростанням частоти зростає і розмір дискретних даних і, отже, складність їхнього оброблення, передачі і зберігання.

При всіх якісних відмінностях між неперервною і дискретною величинами існує чіткий зв'язок, встановлюваний теоремоюдискретизації Шеннона-Котельникова.

Як відомо з відповідного розділу математичного аналізу, будь-яка неперервна функція S(t) може бути розкладеною на скінченному проміжку в ряд Фур’є. Суть цього розкладання полягає в тому, що функція подається у вигляді суми ряду синусоїд з різними амплітудами і фазами, і з кратними частотами. Коефіцієнти (амплітуди) при синусоїдах називаються спектром функції. У гладких функцій спектр швидко спадає (із зростанням номера коефіцієнти швидко прямують до нуля). Для швидко змінюваних функцій спектр спадає поволі, оскільки в сумі гармонічного ряду таких функцій переважають синусоїди з високими частотами.

Вважається, що сигнал має обмежений спектр, якщо після певного номера всі коефіцієнти спектру прямують до нуля. Іншими словами, на заданому проміжку часу сигнал подається у вигляді скінченної суми ряду Фур’є. В цьому випадку говорять, що спектр сигналу знаходиться нижче за граничну частоту f_м, де f_м - частота синусоїди при останньому ненульовому коефіцієнті.

Теорема дискретизації формулюється так:

Неперервна інформація S(t) з обмеженим спектром, тобто така, що має в своєму спектрі складові з частотами, що не перевищують деяку максимальну частоту спектру f_м,, повністю відтворюється послідовністю відліків S(t_i), узятих в дискретні моменти часу з інтервалом .

1.2 Базові поняття теорії інформації

У найзагальнішому розумінні інформація – це передавання, відображення певного різноманіття. В теорії інформації інформацію розглядають як кількісну міру усунення невизначеності, що зменшується у результаті отримання якихось відомостей.

Отже, інформація – це об'єктивно існуючий зміст, який характеризує стан і поведінку певної системи загалом або її окремих елементів та зменшує ступінь невизначеності у процесі його пізнання і переробки. Інформація протилежна невизначеності.

Кодування - перетворення інформації на впорядкований набір символів, елементів, знаків. При кодуванні кожному повідомленню з деякої множини, що називається ансамблем повідомлень, ставиться у відповідність зумовлена кодова комбінація - набір символів (елементів, знаків). Множина повідомлень називається алфавітом повідомлень, або первинним алфавітом, а множина символів (елементів, знаків) називається алфавітом джерела,або вторинним алфавітом. Побудована відповідно до певної схеми кодування множина кодових комбінацій називається кодом. Залежно від алфавіту, що використовується для побудови кодових комбінацій, розрізняють двійкові (бінарні) коди, алфавіт яких складається з двох символів: 0 і 1 і недвійкові (багатопозиційні, q-коди), алфавіт яких містить більшу кількість символів.

За функціональним призначенням коди поділяють на безнадмірні (некоригувальні, первинні, прості ) і надмірні (коригувальні, завадостійкі). Перша група кодів призначена для економного кодування інформації – стиснення. Друга використовується для виявлення та/чи виправлення помилок, що виникають у процесі передачі даних каналом зв'язку із завадами.

Коди можуть бути рівномірними і нерівномірними - з постійною і змінною кількістю розрядів.

Канал зв'язку - це середовище передачі інформації, що характеризується максимально можливою для нього швидкістю передачі даних – пропускною здатністю, або ємністю каналу.

Пропускну здатність каналу зв'язку без шуму можна наближено обчислити, знаючи максимальну частоту хвильових процесів, допустимих у цьому каналі. Вважається, що швидкість передачі даних може бути не менше цієї частоти. Типові канали зв'язку: телеграфний, телефонний, оптоволоконний, цифровий телефонний. Найбільш поширені телефонні лінії зв'язку, для яких досягнута швидкість передачі даних, >50 Кбод.

Шум - це завади в каналі зв'язку.

Узагальнена схема системи передачі інформації має такий вигляд (рис. 1.2).

1.3 Способи вимірювання інформації

Припустимо, що стан деякого об'єкта або системи наперед відомий. Тоді повідомлення про цей стан не несе ніякої інформації для її одержувача. Якщо ж стан об'єкта змінився і джерелом передане якесь інше повідомлення про стан спостережуваного об'єкта, то це повідомлення несе нові відомості, які додадуть знання про об'єкт. Тоді можна говорити, що таке повідомлення містить деяку кількість інформації для її одержувача.

Отже, на якісному інтуїтивному рівні інформацію можна визначити як нове, наперед невідоме знання про стан деякого об'єкта або системи, а кількість інформації - кількість цього знання. Зрозуміло, що якщо нове знання збільшує загальний рівень знань про стан спостережуваного об'єкта, то кількість інформації накопичується і має адитивний характер.

До передачі джерелом повідомлення для його одержувача має місце деяка невизначеність щодо стану об'єкта спостереження. Після вибору повідомлення джерелом утворюється певна кількість інформації, що якоюсь мірою зменшує цю невизначеність.

В основу теорії інформації покладено запропонований Клодом Шенноном спосіб вимірювання кількості інформації, що міститься в одній випадковій величині щодо іншої випадкової величини[1]. Цей спосіб дозволяє виразити кількість інформації числом і надає можливість об'єктивно оцінити інформацію, що міститься у повідомленні.

Коротко розглянемо основні викладки ймовірностного підходу Шеннона до визначення кількості інформації.

Нехай дискретне джерело інформації видає послідовність повідомлень x_i, кожне з яких вибирається з алфавіту x ₁, x ₂, …, x_k, де k - об'єм алфавіту джерела.

У кожному елементарному повідомленні для його одержувача міститься інформація як сукупність відомостей про стан деякого об'єкта або системи.

Для того щоб абстрагуватися від конкретного змісту інформації, тобто її смислового значення, і отримати саме загальне визначення кількості інформації, кількісну міру інформації визначають без урахування її смислового змісту, а також цінності і корисності для одержувача.

До того як зв'язок відбувся, є деяка невизначеність щодо того, яке з повідомлень з можливих буде передане. Ступінь невизначеності передачі х_i можна визначити його апріорною імовірністю p_i. Отже, кількість інформації I(X_i) буде деякою функцією від p_i: I(X_i)=f(p_i). Визначимо вид цієї функції.

Вважатимемо, що міра кількості інформації I(X_i) відповідає двом інтуїтивним властивостям:

1) якщо вибір повідомлення джерела x_i наперед відомий (немає невизначеності), тобто маємо достовірний випадок, імовірність якого p_i= 1, то I(X_i)=f( 1 )= 0;

2) якщо джерело послідовно видає повідомлення x_i і x_j, і імовірність такого вибору p_ij - сумісна імовірність подій x_i і x_j, то кількість інформації в цих елементарних повідомленнях дорівнює сумі кількості інформації в кожному з них.

Ймовірність сумісного випадання двох випадкових подій x_i і x_j дорівнює добутку ймовірності однієї з цих подій на ймовірність іншої за умови, що перша подія відбулася, тобто p_ij=p_i×p_j_/_i=P×Q.

Тоді, з властивості 2 кількості інформації випливає, що

I (X_i, X_j)= I (X_i)+ I (X_j)= f (P ∙ Q)= f (P)+ f (Q).

Звідси випливає, що функції f (p_i) логарифмічна. Таким чином, кількість інформації зв'язана з апріорною імовірністю співвідношенням

,

при цьому коефіцієнт k і основа логарифма можуть бути довільними.

Для того щоб кількість інформаціївизначалася невід'ємним числом, взяте k =-1, а основу логарифма найчастіше вибирають 2, тобто

. (1.1)

У цьому випадку за одиницю кількості інформації так само береться біт. У такий спосіб біт – це кількість інформації в повідомленні дискретного джерела, алфавіт якого складається з двох альтернативних подій, які є апріорно рівноймовірними. Якщо кількість апріорно рівноймовірних подій дорівнює 2⁸, то за одиницю інформації береться байт.

Якщо джерело інформації видає послідовність взаємозалежних повідомлень, то отримання кожного з них змінює ймовірність появи наступних і відповідно кількість інформації у них. У такому випадку кількість інформаціївиражається через умовну ймовірність вибору джерелом повідомлення x_i за умови, що до цього були обрані повідомлення x_i-1, x_i-2 …, тобто

. (1.2)

Кількість інформації I (X) є випадковою величиною, оскільки самі повідомлення випадкові. Закон розподілу ймовірностей I (X) визначається розподілом ймовірностей P (X) ансамблю повідомлень джерела.

Натомість сам Шеннон зазначав, що смисловий зміст (семантика) повідомлень не має ніякого відношення до його теорії інформації, яка цілком базується на положеннях теорії ймовірності. Його спосіб вимірювання інформації наводив на думку про можливість існування способів вимірювання інформації з урахуванням її змісту, тобто семантичної інформації.

Одним із таких способів вимірювання кількості інформації є функція inf (S)=-log₂ p (S), де S - висловлювання, смисловий зміст якого вимірюється; p (S) - ймовірність істинності S. Властивості цієї функції:

1) якщо S ₁ S ₂ істинно, то inf(S₁) ≥ inf(S₂);

2) якщо S істинно, то inf(S)= 0;

3) Inf(S) ≥ 0;

4) Inf(S₁, S₂) = inf(S₁) + inf(S₂) 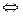p(S₁, S₂)=p(S₁) + p(S₂), тобто S₁, S₂ незалежні.

Приклад. S₁ = “a>3”, S₂ = “a=7”; S₂ S₁, inf(S₂) > inf(S₁).

Значення цієї функції-міри більше для висловлювань, що виключають більшу кількість можливостей.

1. 4 Ентропія джерела. Властивості кількості інформації та ентропії

Кількість інформації, що міститься в одному елементарному повідомленні x_i, не повністю характеризує джерело. Джерело дискретних повідомлень може бути охарактеризовано середньою кількістю інформації, що припадає на одне елементарне повідомлення, і називається ентропією джерела, тобто питомою кількістю інформації

, i =1… k, (1.3)

де k - об'єм алфавіту джерела.

Фізичний зміст ентропії - це середньостатистична міра невизначеності знань одержувача інформації щодо стану спостережуваного об'єкта.

У формулі (1.3) статистичне усереднювання (тобто обчислювання математичного сподівання випадкової величини) виконується за всім ансамблем повідомлень джерела. При цьому необхідно враховувати всі імовірнісні зв'язки між різними повідомленнями. Чим вища ентропія джерела, тим більша кількість інформації в середньому закладається в кожне повідомлення, тим важче її запам'ятати (записати) або передати каналом зв'язку.

Необхідні втрати енергії на передачу повідомлення пропорційні ентропії (середній кількості інформації на одне повідомлення). Звідси випливає, що кількість інформації в послідовності з N повідомлень визначається кількістю цих повідомлень і ентропією джерела, тобто

I (N)= N×H (X).

Ентропія як кількісна міра інформаційності джерела має такі властивості:

1) ентропія дорівнює нулю, якщо хоча б одне з повідомлень достовірне;

2) ентропія завжди більша або дорівнює нулю, є величиною дійсною і обмеженою;

3) ентропія джерела з двома альтернативними подіями може змінюватися від 0 до 1;

4) ентропія - величина адитивна: ентропія джерела, повідомлення якого складаються з повідомлень декількох статистично незалежних джерел, дорівнює сумі ентропій цих джерел;

5) ентропія максимальна, якщо всі повідомлення мають однакову імовірність. Таким чином,

. (1.4)

Вираз (1.4) називається формулою Хартлі. ЇЇ легко вивести з формули Шеннона (1.3), припустивши, що p_i =1/ k, де i= 1… k.

При нерівноймовірних елементарних повідомленнях x_i ентропія зменшується. У зв'язку з цим вводиться така міра джерела, як статистична надлишковість

, (1.5)

де H (X) - ентропія джерела повідомлень; H (X) _max = log ₂ k - максимально досяжна ентропія даного джерела.

Надлишковість джерела (1.5) свідчить про інформаційний резерв повідомлень, елементи яких нерівноймовірні. Вона показує, яка частка максимально можливої при заданому об'ємі алфавіту невизначеності (ентропії) не використовується джерелом.

Існує поняття семантичної надлишковості, яке випливає з того, що будь-яку думку можна сформулювати коротше. Вважається, що якщо яке-небудь повідомлення можна скоротити без втрати його смислового змісту, то воно має семантичну надлишковість.

Розглянемо дискретні випадкові величини (д. в. в.) Х і Y, що задані законами розподілів їхніх ймовірностей P (X=X_i)= p_i, P (Y=Y_i)= q_j та розподілом сумісних ймовірностей системи д. в. в. P (X=X_i, Y=Y_j )= p_ij. Тоді кількість інформації, що міститься в д. в. в. Х щодо д. в. в. Y – взаємна інформація,визначається так:

(1.6)

Для неперервних випадкових величин (в. в.) X і Y, безумовні та сумісна щільності розподілів ймовірностей яких відповідно r_X (t₁), r_Y (t₂) та r_XY (t₁, t₂), взаємну кількість інформації шукають так само, як і в разі д. в. в.:

.

Очевидно, що

і, отже, ,

тобто приходимо до виразу (1.3) знаходження ентропії H (X). Таким чином, ентропія випадкової величиниX:

.

Наведемо властивостікількості інформації і ентропії:

1) I(X, Y)≥0; I(X, Y)=0 Û X і Y незалежні (одна в. в. нічим не описує іншу);

2) I(X, Y) = I(Y, X);

3) НХ =0 Û X=const;

4) I(X, Y)=HX+HY-H(X, Y), де ;

5) I (X, Y) ≤ I(X, X); якщо I(X, Y)=I(X, X) Þ X=f(Y).

Зразки розв'язування задач до розділу 1

Приклад 1 Дискретні випадкові величини (д. в. в.) X₁ та X₂ визначаються підкиданням двох гральних кубиків. Д. в. в. Y = X₁ + X₂. Знайти кількість інформації I (Y, X₁), I (X₁, X₁), I (Y, Y).

Розв'язання

Побудуємо розподіл ймовірностей д. в. в. X ₁ (або X ₂) (табл. 1):

Таблиця 1

X₁

p_i 1/6 1/6 1/6 1/6 1/6 1/6

Звідси знаходимо ентропію д. в. в X ₁, що у даному випадку буде максимальною, оскільки значення рівноймовірні:

HX ₁= HX ₂ = log₂ 6=1+ log₂ 3»1+1,585»2,585 (біт / сим).

Оскільки X ₁ та X ₂ незалежні д. в. в., то їх сумісна ймовірність визначається так:

P (X ₁= i, X ₂= j)= P (X ₁= i)× P (X ₂= j)= 1/36; i = 1... 6, j = 1... 6.

Побудуємо допоміжною таблицю значень д. в. в. Y = X ₁ + X ₂ (табл.2):

Таблиця 2

X ₂ X ₁

Обчислимо ймовірності P (Y=j) (j =2, 3, …, 12):

P (Y= 2)= 1/36; P (Y= 3)= 2×1/36= 1/18; P (Y = 4)= 3×1/36= 1/12;

P (Y= 5)= 4×1/36= 1/9; P (Y= 6)= 5×1/36= 5/36; P (Y= 7)= 6×1/36= 1/6; P (Y= 8) =5×1/36= 5/36; P (Y= 9) =4×1/36= 1/9; P (Y= 10)= 3×1/36= 1/12; P (Y= 11)= 2×1/36= 1/18; P (Y= 12)= 1/36;

Скориставшись допоміжною таблицею (табл.2), запишемо безумовний закон розподілу д. в. в. Y (табл. 3):

Таблиця 3

Y_j

q_j 1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36

Звідси знаходимо ентропію д. в. в. Y так:

(біт/сим)

Побудуємо таблицю розподілу ймовірностей системи д. в. в. (X ₁, Y) p_ij = P (X ₁= i, Y = j) (табл. 4).

Таблиця 4

X ₁ Y

1/36 1/36 1/36 1/36 1/36 1/36

1/36 1/36 1/36 1/36 1/36 1/36

1/36 1/36 1/36 1/36 1/36 1/36

1/36 1/36 1/36 1/36 1/36 1/36

1/36 1/36 1/36 1/36 1/36 1/36

1/36 1/36 1/36 1/36 1/36 1/36

1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36

Тоді взаємна ентропія д. в. в. X ₁, Y

= log₂ 36=2 log₂ 6=2(1+ log₂ 3)»2+

+2×1,585»5,17 (біт / сим).

Кількість інформації, що містить д. в. в. Y стосовно д. в. в. X ₁, обчислимо за формулою . Отже,

(біт/сим).

Кількість інформаціїI (Y, X₁) здебільшого зручніше знайти, скориставшись властивістю 4 кількості інформації і ентропії:

.

Оскільки Y = X ₁+ X ₂, де X ₁ та X ₂ – незалежні д. в. в., то

.

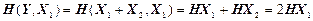(біт/сим).

Відповідь: 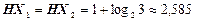(біт/сим);

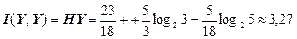(біт/сим);

(біт/сим).

Приклад 2 Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z та кількість інформації, що містить д. в. в. стосовно X та Y. X, Y – незалежні д. в. в., які задаються такими розподілами (табл. 1, табл. 2):

Таблиця 1 Таблиця 2

X Y

p 1/8 1/8 1/4 1/2 q 1/4

Розв'язання

Скориставшись відповідним рядом розподілу ймовірностей д. в. в. X та Y, знаходимо їх ентропії.

Ентропія д. в. в. X

(біт/сим).

Ентропія д. в. в. Y (біт/сим).

Побудуємо допоміжну таблицю значень д. в. в. Z = ½ X - Y ½ та їх ймовірностей (табл. 3). Оскільки X та Y – незалежні д. в. в., то сумісна ймовірність випадання пар значень (x_i, y_j) .

Таблиця 3

X Y

1/8

1/32 1/32 1/32 1/32

1/8

1/32 1/32 1/32 1/32

1/4

1/16 1/16 1/16 1/16

1/2

1/8 1/8 1/8 1/8

1/4 1/4 1/4 1/4

Знайдемо ймовірності системи д. в. в. (Z = j, X = i, , ):

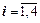P (Z =0, X =1)= 1/32, P (Z =1, X =1)= 1/32, P (Z =2, X =1)= 1/32, P (Z =3, X =1)= 1/32; P (Z =0, X =2)= 1/32, P (Z =1, X =2)= 1/32 + 1/32=1/16, P (Z =2, X =2)= 1/32, P (Z =3, X =2)= 0; P (Z =0, X =3)= 1/16, P (Z =1, X =3)= 1/16 + 1/16=1/8, P (Z =2, X =3)= 1/16, P (Z =3, X =3)= 0; P (Z =0, X =4)= 1/8, P (Z =1, X =4) =1/8, P (Z =2, X =4)= 1/8, P (Z =3, X =4)= 1/8.

Побудуємо таблицю розподілу ймовірностей системи д. в. в.(X, Z) (табл. 4).

Таблиця 4

X Z

1/32 1/32 1/32 1/32 1/8

1/32 1/16 1/32 1/8

1/16 1/8 1/16 1/4

1/8 1/8 1/8 1/8 1/2

1/4 11/32 1/4 5/32

Тоді взаємна ентропія д. в. в. Z та X

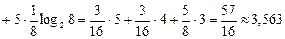(біт/сим).

Скориставшись табл. 3 або табл. 4, побудуємо розподіл ймовірностей д. в. в. Z (табл. 5).

Таблиця 5

Z

p_i 1/4 11/32 1/4 5/32

Звідси знаходимо ентропію д. в. в. Z:

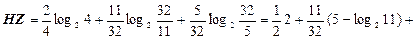
(біт/сим).

Кількість інформації, що містить д. в. в. Z стосовно д. в. в. X, знаходимо, скориставшись властивістю 4 кількості інформації і ентропії:

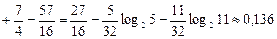(біт/сим).

Побудуємо таблицю розподілу ймовірностей системи д. в. в.(Y, Z) (табл. 6). Для цього, скориставшись табл. 3, обчислимо ймовірності:

P (Z =0, Y =1)= 1/32, P (Z =1, Y =1)= 1/32, P (Z =2, Y =1)= 1/16, P (Z =3, Y =1)= 1/8; P (Z =0, Y =2)= 1/32, P (Z =1, Y =2)= 1/32 + 1/16=3/32, P (Z =2, Y =2)= 1/8, P (Z =3, Y =2)= 0; P (Z =0, Y =3)= 1/16, P (Z =1, Y =3)= 1/32 + 1/8=5/32, P (Z =2, Y =3)= 1/32, P (Z =3, Y =3)= 0; P (Z =0, Y =4)= 1/8, P (Z =1, Y =4) =1/16, P (Z =2, Y =4)= 1/32, P (Z =3, Y =4)= 1/32.

Таблиця 6

Y Z

1/32 1/32 1/16 1/8 1/4

1/32 3/32 1/8 1/4

1/16 5/32 1/32 1/4

1/8 1/16 1/32 1/32 1/4

1/4 11/32 1/4 5/32

Тоді взаємна ентропія д. в. в. Z та Y

(біт/сим).

Отже, кількість інформації, що містить д. в. в. Z стосовно д. в. в. Y

(біт/сим).

Відповідь: HX = 1,75 (біт / сим); HY = 2 (біт / сим); (біт/сим);

(біт/сим);

(біт/сим).

Задачі до розділу 1

1 Дискретні випадкові величини (д. в. в.) X₁ та X₂ визначаються підкиданням двох ідеальних тетраедрів, грані яких позначені числами від 1 до 4. Знайти, скільки інформації про д. в. в. X₁ містить д. в. в. Z = X₁ * X₂, а також ентропію HZ.

2 Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z = X + Y стосовно д. в. в. Y. X та Y незалежні д. в. в., задані такими розподілами:

X Y -2 .

P 1/8 1/8 1/4 1/2 P 3/8 5/8

3 Дискретні випадкові величини (д. в. в.) X₁ та X₂ визначаються підкиданням двох ідеальних тетраедрів, грані яких позначені числами від 1 до 4. Д. в. в. Y дорівнює сумі чисел, що випали при підкиданні цих тетраедрів, тобто Y=X₁+X₂. Знайти кількість взаємної інформації I (X, Y), ентропії HX₁, HY.

4 Дискретна випадкова величина (д. в. в.) X визначається кількістю очок, які випадуть при підкиданні грального кубика, а д. в. в. Y =0, якщо кількість очок, що випали, непарна, і Y =1, якщо кількість очок парна. Знайти кількість інформації I (X, Y) та I (Y, Y).

5 Скільки інформації про дискретну випадкову величину (д. в. в.) X₁ містить д. в. в. Z =(X₁ +1)²- X₂, якщо незалежні д. в. в. X₁ та X₂ можуть із однаковою ймовірністю набувати значень 0 або 1? Знайти ентропії HX₁, HZ. Який характер залежності між д. в. в. X₁ та Z?

6 Значення дискретних випадкових величин (д. в. в.) X₁ та X₂ визначаються підкиданням двох ідеальних монет, а д. в. в. Y – кількість «гербів», що випали на монетах. Знайти ентропії HX₁, HY. Скільки інформації про д. в. в. X₁ містить д. в. в. Y?

7 Дискретні випадкові величини (д. в. в.) X ₁, X ₂ залежні й можуть із однаковою ймовірністю набувати значення 0 або 1. Знайти кількість взаємної інформації I (X ₁, X ₂), якщо сумісний розподіл ймовірностей системи д. в. в. X ₁, X ₂ такий:

X₁ .

X₂

P 1/3 1/6 1/6 1/3

8 Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z = X * Y стосовно X та Y. X, Y – незалежні д. в. в., задані такими розподілами:

X Y -2 .

P 1/8 1/8 1/4 1/2 P 3/8 5/8

9 Значення дискретних випадкових величин (д. в. в.) X ₁ та X ₂ визначаються підкиданням двох ідеальних монет, а д. в. в. Y може набувати два значення: 1, якщо хоча б на одній з монет випав «герб», і 0 - в іншому випадку. Знайти ентропії д. в. в. X ₁ та Y. Скільки інформації про X ₁ містить д. в. в. Y?

10 Дискретна випадкова величина (д. в. в.) X ₁ з однаковими ймовірностями може набувати значень -1, 0, 1, а д. в. в. X ₂ з однаковими ймовірностями – значень 0, 1. X ₁ та X ₂ – незалежні д. в. в., Y = X ₁²+ X ₂². Знайти кількість взаємної інформації I (Y, X ₁), I (Y, X ₂) та ентропії HX ₁, HX ₂, HY.

11 Знайти ентропії д. в. в. X, Y, Z і кількість інформації, що містить д. в. в. Z =2 X + Y стосовно X та Y. X, Y – незалежні д. в. в., задані такими розподілами ймовірностей:

X -1 Y .

P 1/4 1/2 1/4 P 1/6 2/3 1/6

12 Дискретні випадкові величини (д. в. в.) X ₁ та X ₂ визначаються підкиданням двох ідеальних тетраедрів, грані яких позначені числами від 1 до 4. Знайти, скільки інформації про X ₁ містить д. в. в. Z =2 X ₁+ X ₂, а також ентропії HZ, HX.

13 Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z = X ²+ Y ² стосовно X та стосовно Y. X, Y – незалежні д. в. в., задані такими розподілами ймовірностей:

X Y .

P 1/4 P 1/4

14 Дискретна випадкова величина (д. в. в.) X з різною ймовірністю може набувати значень від 1 до 8. Д. в. в. Y набуває значення 0, якщо X парне, і 1, якщо X непарне. Знайти кількість інформації I (Y, X) і ентропію HX, якщо д. в. в. X задана таким розподілом ймовірностей:

X .

P 0,1 0,2 0,1 0,05 0,1 0,05 0,3 0,1

15 Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z = ½ X - Y ½ стосовно X та стосовно Y. X, Y – незалежні д. в. в., задані такими розподілами:

X Y .

P 1/8 1/8 1/4 1/2 P 1/8 1/2 1/4 1/8

16 Скільки інформації про X ₁ та X ₂ містить дискретна випадкова величина (д. в. в.) Z = X ₁²+ X ₂, якщо незалежні д. в. в. X ₁, X ₂ можуть з однаковою ймовірністю набувати значення –1 або 1? Знайти ентропії HX ₁ та HZ.

17 Дискретна випадкова величина (д. в. в.) X₁ може набувати три значення: -1, 0 і 1 з однаковими ймовірностями. Д. в. в. X₂ з однаковими ймовірностями може набувати значення 0, 1 і 2. X₁ і X₂ – незалежні, Y = X₁ ²+ X₂. Знайти кількість інформації I (X₁, Y), I (X₂, Y) і ентропії HX₁, HX₂, HY.

Розділ 2 ХАРАКТЕРИСТИКИ ДИСКРЕТНОГО КАНАЛУ ПЕРЕДАЧІ ІНФОРМАЦІЇ

2.1 Умовна ентропія

Раніше отримана формула ентропії (1.3) визначає її середньою кількістю інформації, що припадає на одне повідомлення джерела статистично незалежних повідомлень. Така ентропія називається безумовною.

Як відомо з відповідного розділу математичної статистики, мірою порушення статистичної незалежності повідомлень x і у є умовна ймовірністьp (x/y) появи повідомлення x_i за умови, що вже вибрано повідомлення y_j або умовна ймовірність появи повідомлення y_j, якщо вже отримане повідомлення x_i, причому в загальному випадку p (x / y)¹ p (y / x).

Умовну ймовірність можна отримати з безумовної ймовірності p (x) чи p (y) та сумісної ймовірності системи в. в. p (x, y) за формулою множення ймовірностей:

p (x, y)= p (x)× p (y / x), (1.7)

p (x, y)= p (y)× p (y / x), (1.8)

звідси

,

.

В окремому випадку для статистично незалежних повідомлень маємо: p (y/x)= p (y), p (x/y)= p (x).

При існуванні статистичної залежності між повідомленнями джерела факт вибору одного з повідомлень зменшує або збільшує ймовірності вибору інших повідомлень до умовних ймовірностей. Відповідно змінюється й кількість інформації, що міститься в кожному з цих повідомлень, згідно з (1.2). Ентропія такого джерела також змінюється відповідним чином, причому обчислюється ентропія за тією самою формулою (1.3), але вже з урахуванням умовних ймовірностей. Така ентропія називається умовною.

2.2 Модель системи передачі інформації

Розглянемо модельсистеми спостереження, перетворення, збору і зберігання інформації, що складається з двох джерел, між повідомленнями яких існує статистичний взаємозв'язок. Нехай джерело X задано моделлю - ансамблем повідомлень { x₁, x₂, …, x_i, …, x_k } і рядомрозподілу P (X) їхніх ймовірностей, а джерело Y - ансамблем { y₁, y₂, …, y_j, …, y_l } і розподілом P(Y).

Ніяких обмежень на алфавіти X і Y н