Из теории математической обработки геодезических измерений известно, что точность пунктов любой геодезической сети определяется следующей вариационной матрицей:
К=σ  * N
* N  , (1)
, (1)
где:
N – матрица нормальных уравнений при уравнивании параметрическим способом;
σ – стандарт единицы веса, соответствующий измерению, вес которого равен единице.
В данном случае можно приять, что с весом равным единице измеряются направления. Тогда σ – это стандарт измерения направлений, которые необходимо рассчитать.
Для такого расчета должны быть известны элементы матрицы К и матрицы N.
Матрица К характеризует точность определения положения пунктов полигонометрии.
А. Вычисление матрицы нормальных уравнений.
Матрица N вычисляется по известной формуле:
N=A  РА, (2)
РА, (2)
где:
А – матрица уравнений поправок измерений;
Р – диагональная матрица весов измерений.
Поскольку в полигонометрии измеряются горизонтальные углы и расстояния, то уравнение поправок составляется для них. Горизонтальный угол можно рассматривать как разность направлений. Тогда вместо одного уравнения поправок горизонтального угла составляют два уравнения поправок направлений.
Уравнение поправок для направления между пунктами 1 и 2 имеет вид:
ν = - δ  + aδx
+ aδx 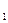 - bδy
- bδy 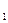 - aδx
- aδx 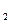 + bδy
+ bδy 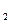 +l
+l  , (3)
, (3)
где:
a= 206265” sinα/S, (4)
b= 206265” соsα/S (5)
δz 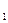 - поправка в ориентирующий угол;
- поправка в ориентирующий угол;
δx 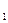 , δy
, δy 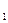 , δx
, δx 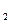 , δy
, δy 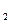 - поправки в приближенные значения координат определяемых пунктов;
- поправки в приближенные значения координат определяемых пунктов;
α – дирекционный угол;
S  - длина линии между точками 1 и 2 в сантиметрах;
- длина линии между точками 1 и 2 в сантиметрах;
Уравнение поправок сторон записывается так:
ν = -cosα δx 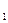 -sinα δy
-sinα δy 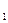 +cosα δx
+cosα δx 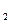 +sinα δy
+sinα δy 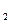 + l
+ l  , (6)
, (6)
где:
l  - свободный член уравнения поправок сторон.
- свободный член уравнения поправок сторон.
Исходя из (2) следует, что матрица А составляется лишь из коэффициентов при неизвестных уравнениях (3) и (6). Величина свободного члена здесь значения не имеет. Для проектных расчетов значения дирекционного угла α и длины стороны S необходимы с точностью соответственно до градуса и миллиметра на плане. Их можно снять с проекта полигонометрического хода на схеме расположения кадастровых районов и кварталов.
Таблица 1. Значение дирекционных углов, длин сторон и коэффициентов уравнений поправок полигонометрического хода.
| Направления | Дирекц углы | длины сторон, см | a | b | cos | sin |
| B-E | 8,0 | -5,6 | -0,57 | 0,82 | ||
| E-B | -8,0 | 5,6 | 0,57 | -0,82 | ||
| E-F | -2,6 | -13,5 | -0,98 | -0,19 | ||
| F-E | 2,6 | 13,5 | 0,98 | 0,19 | ||
| F-C | 3,5 | -4,2 | -0,77 | 0,64 | ||
| C-F | -3,5 | 4,2 | 0,77 | -0,64 |
Таблица2. Уравнение поправок измерений для проектного хода полигонометрии.
| dXE | dYE | dXF | dYF | |||||
| станция | наб пункты | z | a | b | c | d | S | p |
| B | E | -1 | -8,05 | -5,63 | 0,00 | 0,00 | -13,68 | 1,00 |
| A | -1 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 1,00 | |
| -2z1 | -8,05 | -5,63 | 0,00 | 0,00 | -13,68 | -0,50 | ||
| E | B | -1 | -8,05 | -5,63 | 0,00 | 0,00 | -13,68 | 1,00 |
| F | -1 | -2,62 | 13,50 | 2,62 | -13,50 | 0,00 | 1,00 | |
| -2z2 | -10,67 | 7,86 | 2,62 | -13,50 | -13,68 | -0,50 | ||
| F | C | -1 | 0,00 | 0,00 | 3,49 | 4,16 | 7,65 | 1,00 |
| E | -1 | -2,62 | 13,50 | 2,62 | -13,50 | 0,00 | 1,00 | |
| -2z3 | -2,62 | 13,50 | 6,11 | -9,34 | 7,65 | -0,50 | ||
| C | D | -1 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 1,00 |
| F | -1 | 0,00 | 0,00 | 3,49 | 4,16 | 7,65 | 1,00 | |
| -2z4 | 0,00 | 0,00 | 3,49 | 4,16 | 7,65 | -0,50 | ||
| B-E | -0,57 | 0,82 | 0,00 | 0,00 | 0,25 | 0,25 | ||
| E-F | 0,98 | 0,19 | -0,98 | -0,19 | 0,00 | 0,25 | ||
| F-C | 0,00 | 0,00 | 0,77 | -0,64 | 0,12 | 0,25 |
В таблице 3 представлена матрица коэффициентов нормальных уравнений (2).
Таблица 3. Матрица коэффициентов нормальных уравнений.
| a | b | c | d | s |
| 50,8 | 56,8 | 8,0 | -13,5 | 102,1 |
| 290,2 | 19,2 | -248,3 | 117,8 | |
| 10,3 | -2,9 | 34,6 | ||
| 255,7 | -8,9 |






