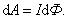Участок цепи, на котором не действуют сторонние силы, приводящие к возникновению электродвижущей силы (рис. 1), называется однородным.
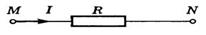Рис. 1
Закон Ома для однородного участка цепи был установлен экспериментально в 1826 г. Г. Омом.
Согласно этому закону, сила тока I в однородном металлическом проводнике прямо пропорциональна напряжению U на концах этого проводника и обратно пропорциональна сопротивлению R этого проводника:
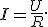
На рисунке 2 изображена схема электрической цепи, позволяющая экспериментально проверить этот закон. В участок MN цепи поочередно включают проводники, обладающие различными сопротивлениями.
Рис. 2
Напряжение на концах проводника измеряется вольтметром и может изменяться с помощью потенциометра. Силу тока измеряют амперметром, сопротивление которого ничтожно мало (RA ≈ 0). График зависимости силы тока в проводнике от напряжения на нем — вольт-амперная характеристика проводника — приведен на рисунке 3. Угол наклона вольт-амперной характеристики зависит от электрического сопротивления проводника R (или его электропроводимости G):.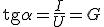 
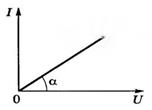Рис. 3
Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:
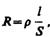
где r — коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — ом×метр (Ом×м).
30. Закон Ома для неоднородного участка цепи и для замкнутой цепи.
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.
Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.
Рис. 1
Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δφ. Разность потенциалов на концах участка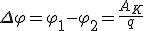 
, где AK — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению, 
, где q — положительный заряд, который перемещается между любыми двумя точками цепи; 
— разность потенциалов точек в начале и конце рассматриваемого участка; 
. Тогда говорят о напряжении для напряженности: Eстац. э. п. = Eэ/стат. п. + Eстор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:
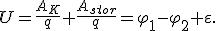
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то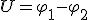 
. Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид: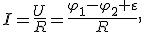 
где R — общее сопротивление неоднородного участка.
Электродвижущая сила (ЭДС ) ε может быть как положительной, так и отрицательной. Это связано с полярностью включения электродвижущая сила (ЭДС ) в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε < 0.
31. Закон Ома в дифференциальной форме.
Закон Ома для однородного участка цепи, все точки которого имеют одинаковую температуру, выражается формулой (в современных обозначениях):
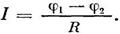
В таком виде формула закона Ома справедлива только для проводников конечной длины, так как входящие в это выражение величины I и U измеряются приборами, включенными на этом участке.
Сопротивление R участка цепи зависит от длины l этого участка, поперечного сечения S и удельного сопротивления проводника ρ. Зависимость сопротивления от материала проводника и его геометрических размеров выражается формулой:
которая справедлива только для проводников постоянного сечения. Для проводников переменного сечения соответствующая формула не будет столь простой. В проводнике переменного сечения сила тока в различных сечениях будет одинаковой, однако плотность тока будет разной не только в различных сечениях, но даже и в различных точках одного и того же сечения. Различное значение будет иметь и напряженность, а, следовательно, и разность потенциалов на концах различных элементарных участков. Усредненные значения I, U и R по всему объему проводника не дают информации об электрических свойствах проводника в каждой его точке.
Для успешного изучения электрических цепей необходимо получить выражение закона Ома в дифференциальной форме с тем, чтобы оно выполнялось в любой точке проводника любой формы и любых размеров.
Зная связь напряженности электрического поля с разностью потенциалов на концах некоторого участка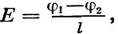 
, зависимость сопротивления проводника от его размеров и материала и используя закон Ома для однородного участка цепи в интегральной форме 
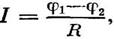найдем: 
Обозначив 
где σ — удельная электропроводность вещества, из которого сделан проводник, получим:
где 
— плотность тока. Плотность тока — это вектор, направление которого совпадает с направлением вектора скорости перемещения положительных зарядов. Полученное выражение в векторной форме будет иметь вид:
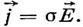
Оно выполняется в любой точке проводника, по которому течет электрический ток. Для замкнутой цепи следует учесть тот факт, что в ней, кроме напряженности поля кулоновских сил, действуют сторонние силы, создающие поле сторонних сил, характеризующееся напряженностью Ест. С учетом этого закон Ома для замкнутой цепи в дифференциальной форме будет иметь вид:
32. Разветвленные электрические цепи. Правила Кирхгофа.
Расчет разветвленных цепей упрощается, если пользоваться правилами Кирхгофа. Первое правило относится к узлам цепи. Узлом называется точка, в которой сходится более чем два тока. Токи, текущие к узлу, считается имеют один знак (плюс или минус), от узла - имеют другой знак (минус или плюс).
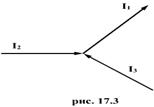
Первое правило Кирхгофа является выражением того факта, что в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды и формулируется в следующем виде: алгебраическая сумма токов, сходящихся в узле, равна нулю
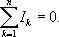
Второе правило Кирхгофа является обобщением закона Ома на разветвленные электрические цепи.
Рассмотрим произвольный замкнутый контур в разветвленной цепи (контур 1-2-3-4-1) (рис. 1.2). Зададим обход контура по часовой стрелке и применим к каждому из неразветвленных участков контура закон Ома.
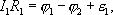
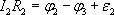
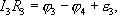
Сложим эти выражения, при этом потенциалы сокращаются и получаем выражение
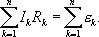
В любом замкнутом контуре произвольной разветвленной электрической цепи, алгебраическая сумма падений напряжений (произведений сил токов на сопротивление) соответствующих участков этого контура равна алгебраической сумме эдс входящих в контур.
33. Работа и мощность постоянного тока. Закон Джоуля-Ленца.
Работа тока - работа электрического поля по переносу электрических зарядов вдоль проводника;
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.
Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:
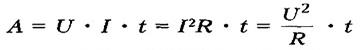
По закону сохранения энергии:
работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия
равна работе тока.
В системе СИ:
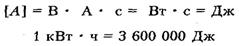
ЗАКОН ДЖОУЛЯ -ЛЕНЦА
При прохождении тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.
Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
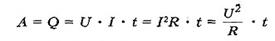
По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.
В системе СИ:
[Q] = 1 Дж
МОЩНОСТЬ ПОСТОЯННОГО ТОКА
- отношение работы тока за время t к этому интервалу времени.
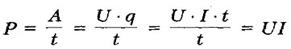
В системе СИ:
34. Магнитное поле постоянного тока. Силовые линии. Индукция магнитного поля в вакууме.
35. Закон Био-Савара-Лапласа. Принцип суперпозиции.
Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен
(1)
где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.
Модуль вектора dB задается выражением
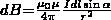(2)
где α — угол между векторами dl и r.
Аналогично электрическому, для магнитного поля выполняется принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
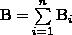(3)
Используя данные формулы для расчет характеристик магнитного поля (В и Н) в общем случае достаточно сложен. Однако если распределение тока имеет какую-либо симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции дает возможность просто рассчитать некоторые поля.
36. Магнитное поле прямолинейного проводника с током.
Линии магнитной индукции магнитного поля прямолинейного тока представляют собой концентрические окружности, расположенные в плоскости, перпендикулярной к проводнику, с центром на оси проводника. Направление линий индукции определяется правилом правого винта: если поворачивать головку винта так, чтобы поступательное движение острия винта происходило вдоль тока в проводнике, то направление вращения головки указывает направление линий магнитной индукции поля прямого проводника с током.
На рисунке 1, а прямолинейный проводник с током расположен в плоскости рисунка, линии индукции — в плоскости, перпендикулярной рисунку. На рисунке 1, б изображено сечение проводника, расположенного перпендикулярно плоскости рисунка, ток в нем направлен от нас (это обозначается крестиком "х"), линии индукции располагаются в плоскости рисунка.
Рис. 1
Как показывают расчеты, модуль магнитной индукции поля прямолинейного тока может быть рассчитан по формуле
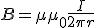
где μ — магнитная проницаемость среды, μ0 = 4π·10-7 H/A2 — магнитная постоянная, I — сила тока в проводнике, r — расстояние от проводника до точки, в которой вычисляется магнитная индукция.
Магнитная проницаемость среды — это физическая величина, показывающая, во сколько раз модуль магнитной индукции В поля в однородной среде отличается от модуля магнитной индукции B0 в той же точке поля в вакууме:
Магнитное поле прямого проводника с током — поле неоднородное.
37. Магнитное поле кругового витка с током.
Согласно закону Био-Савара-Лапласа, индукция магнитного поля, создаваемого элементом тока dl на расстоянии r от него есть
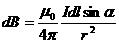
где α – угол между элементом тока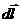 
и радиус-вектором 
, проведенным из этого элемента в точку наблюдения; r - расстояние от элемента тока до точки наблюдения.
В нашем случае α = π/2, sinα = 1; 
, где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы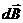 
образуют в этой точке конус с углом раствора при вершине 2 
= π - 2β, где β – угол между отрезками а и r.
Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка:
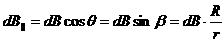
Результирующую величину индукции магнитного поля B на оси витка получим, проинтегрировав это выражение по длине контура от 0 до 2πR:
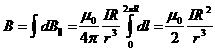
или, подставив значение r:
В частности, при а = 0 находим индукцию магнитного поля в центре кругового витка с током:
Этой формуле можно придать другой вид, воспользовавшись определением магнитного момента витка с током:
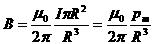
Последнюю формулу можно записать в векторном виде (см. рис.9.1):
.
38. Действие магнитного поля на проводник с током. Закон Ампера.
Магнитное поле действует с некоторой силой на любой проводник с током, находящийся в нем.
Если проводник, по которому протекает электрический ток подвесить в магнитном поле, например, между полюсами магнита, то магнитное поле будет действовать на проводник с некоторой силой и отклонять его.
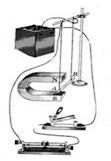
Направление движения проводника зависит от направления тока в проводнике и от расположения полюсов магнита.
Сила, с которой магнитное поле действует на проводник с током, называется силой Ампера.
Французский физик А. М. Ампер был первым, кто обнаружил действие магнитного поля на проводник с током. Правда, источником магнитного поля в его опытах был не магнит, а другой проводник с током. Помещая проводники с током рядом друг с другом, он обнаружил магнитное взаимодействие токов (рис. 67) - притяжение параллельных токов и отталкивание антипараллельных (т. е. текущих в противоположных направлениях). В опытах Ампера магнитное поле первого проводника действовало на второй проводник, а магнитное поле второго проводника - на первый. В случае параллельных токов силы Ампера оказывались направленными навстречу друг другу и проводники притягивались; в случае антипараллельных токов силы Ампера изменяли свое направление и проводники отталкивались друг от друга.
Направление силы Ампера можно определить с помощью правила левой руки:
если расположить левую ладонь руки так, чтобы четыре вытянутых пальца указывали направление тока в проводнике, а силовые линии магнитного поля входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник с током (рис. 68).
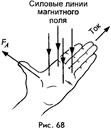
Эта сила (сила Ампера) всегда перпендикулярна проводнику, а также силовым линиям магнитного поля, в котором этот проводник находится.
Сила Ампера действует не при любой ориентации проводника. Если проводник с током расположить вдоль си
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила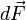 
, с которой магнитное поле действует на элемент объёма 
проводника с током плотности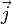 
, находящегося в магнитном поле с индукцией: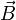 
. 
Если ток течёт по тонкому проводнику, то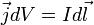 
, где — 
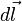«элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Сила 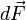, с которой магнитное поле действует на элемент 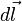проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока 
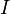в проводнике и векторному произведению элемента длины 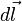проводника на магнитную индукцию: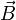
. 
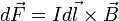
Направление силы 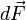определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила правой руки.
Модуль силы Ампера можно найти по формуле:
, 
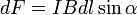
где 
— угол между векторами магнитной индукции и тока.
Сила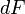 
максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции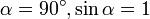 
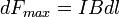
39. Взаимодействие прямолинейных параллельных токов.
Закон Ампера используется при нахождении силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2; (направления токов даны на рис. 1), расстояние между которыми R. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на соседний проводник с током. Найдем, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Магнитное поле тока I1 есть линии магнитной индукции, представляющие собой концентрические окружности. Направление вектора B1 задается правилом правого винта, его модуль есть
Направление силы dF1, с которой поле B1 действует на участок dl второго тока, находится по правилу левой руки и указано на рисунке. Модуль силы, используя (2), с учетом того, что угол α между элементами тока I2 и вектором B1 прямой, будет равен
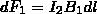
подставляя значение для В1, найдем
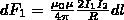(3)
Аналогично рассуждая, можно показать, что сила dF2 с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна
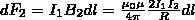(4)
Сопоставление выражений (3) и (4) дает, что
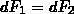
т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой, равной
(5)
Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением (5).
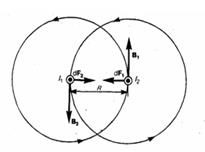Рис.1
40. Магнитное поле движущего электрического заряда.
Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд порождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой
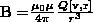(1)
где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.
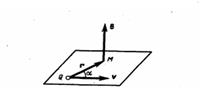Рис.1
Модуль вектора магнитной индукции (1) находится по формуле
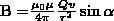(2)
где α — угол между векторами v и r.
Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: 
Приведенные законы (1) и (2) выполняются лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле движущегося с постоянной скорость заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, который находится в той точке, где в данный момент времени находится движущийся заряд.
Формула (1) задает магнитную индукцию положительного заряда, движущегося со скоростью v. При движении отрицательнго заряда Q заменяется на -Q. Скорость v - относительная скорость, т. е. скорость относительно системы отсчета наблюдателя. Вектор В в данной системе отсчета зависит как от времени, так и от расположения наблюдателя. Поэтому следует отметить относительный характер магнитного поля движущегося заряда.
41. Теорема о циркуляции вектора индукции магнитного поля.
Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление обхода контура. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую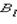 
вектора 
в данном месте, то есть определить проекцию вектора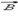 
на направление касательной к данному участку контура (рис. 4.17.2). 2
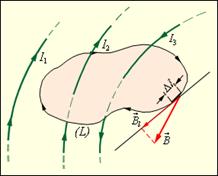
Рисунок 4.17.2. Замкнутый контур (L) с заданным направлением обхода. Изображены токи I1, I2 и I3, создающие магнитное поле.
Циркуляцией вектора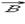 
называют сумму произведений 
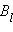Δl, взятую по всему контуру L:
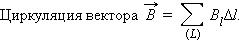
Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура. Теорема о циркуляции утверждает, что циркуляция вектора 
магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
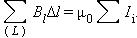
В качестве примера на рис. 4.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I2 и I3 пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I3 > 0, а I2 < 0. Ток I1 не пронизывает контур L. Теорема о циркуляции в данном примере выражается соотношением:
Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции. Простейшим примером применения теоремы о циркуляции является определение магнитной индукции поля прямолинейного проводника с током. Учитывая симметрию в данной задаче, контур L целесообразно выбрать в виде окружности некоторого радиуса R, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии вектор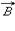 
направлен по касательной (
), а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению:
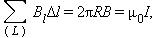
откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее. Этот пример показывает, что теорема о циркуляции вектора магнитной индукции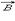 
может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля. Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки (рис. 4.17.3).
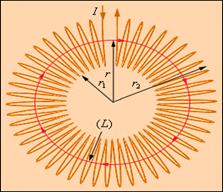
Рисунок 4.17.3. Применение теоремы о циркуляции к тороидальной катушке.
Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рис. 4.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 4.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора 
одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:B ∙ 2πr = μ0IN,
где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,
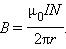
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r2 – r1 << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае B = μ0In.
42. Магнитное поле бесконечного прямолинейного проводника с током и бесконечно длинного соленоида.
Каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки. На рис. 4.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида.
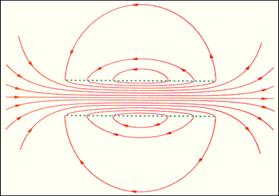
Рисунок 4.17.4. Магнитное поле катушки конечной длины. В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки.
В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис. 4.17.5.
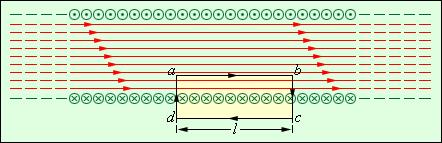
Рисунок 4.17.5. Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоида.
Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора 
по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен Inl. Согласно теореме о циркуляции,Bl = μ0Inl,
Откуда B = μ0In.
43. Поток индукции магнитного поля. Теорема Остроградского-Гауса для магнитного поля.
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна
(1)
где Bn=Вcosα - проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), dS=dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.
Поток вектора магнитной индукции ФB через произвольную заданную поверхность S равен
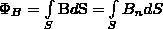(2)
Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В, Bn=B=const и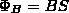 
Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит сквозь плоскую поверхность площадью 1 м2, который расположен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл•м2).
Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:
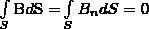(3)
Эта теорема является отражением факта, что магнитные заряды отсутствуют, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Следовательно, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы.
В качестве примера найдем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ, равна
Магнитный поток сквозь один виток соленоида площадью S равен
а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением,
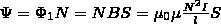
44. Работа перемещения проводника и контура с током в магнитном поле.
Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле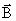 
, перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор 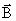сонаправлен с. 
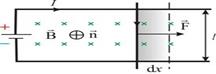Рис. 2.17
На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:
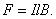
Пусть проводник l переместится параллельно самому себе на расстояние dx. При этом совершится работа:
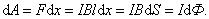
Итак,
, 
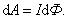(2.9.1)
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток 
, пронизывающий контур, направлен по нормали 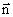к контуру, поэтому.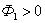 
Рис. 2.18
Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком. 
Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком. 
Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
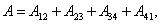
где, 
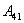равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).
Провод 1–2 перерезает поток (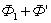
), но движется против сил действия магнитного поля.
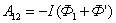
Тогда общая работа по перемещению контура
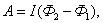или
, 
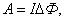(2.9.2)
здесь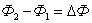 
– это изменение магнитного потока, сцепленного с контуром.
Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.
Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле
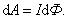, (2.9.5)
Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины dФ различен.
Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется 
, то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу
