Отсюда напряжённость электрического поля на расстоянии r от центра заряженной сферы равна
Сравнивая (5.7) с (5.2), приходим к выводу, что напряжённость электрического поля заряженного шара равна напряжённости такого же точечного заряда, расположенного в центре шара.
13. Напряженность электростатического поля шара. Равномерно заряженного по объему.
Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ = dQ/dV – заряд, который приходится на единицу объема). Учитывая соображения симметрии, аналогичные п.3, можно доказать, что для напряженности поля вне шара получится тот же результат, что и в случае (3). Внутри же шара напряженность поля будет иная. Сфера радиуса r'<R охватывает заряд Q'=(4/3)πr'3ρ. Поэтому, используя теорему Гаусса, 4πr'2E=Q'/ε0=(4/3)πr'3ρ/ε0. Т.к. ρ=Q/(4/3πR3)) получаем
4)
Значит, напряженность поля вне равномерно заряженного шара описывается формулой (3), а внутри его изменяется линейно с расстоянием r' согласно зависимости (4). График зависимости Е от r для рассмотренного случая показан на рис. 5.
14. Работа сил электростатического поля по перемещению заряда.
Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда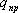 
из одной точки электростатического поля в другую на отрезке пути 
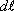, по определению равна
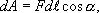
где 
- угол между вектором силы F и направлением движения 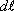. Если работа совершается внешними силами, то dA0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда 
из точки “а” в точку “b” будет равна
где 
- кулоновская сила, действующая на пробный заряд 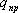в каждой точке поля с напряженностью Е. Тогда работа
Пусть заряд 
перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии 
в точку “b”, удаленную от q на расстоянии 
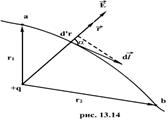
Как видно из рисунка 
тогда получим
Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно
15. Теорема о циркуляции вектора напряженности электростатического поля.
Существуют два равнозначных определения консервативной силы. Оба они подробно обсуждались в механике.
Консервативной называется сила, работа которой не зависит от формы траектории.
Консервативной называется сила, работа которой на замкнутой траектории равна нулю.
Рассмотрим перемещение заряда q в электростатическом поле 
по замкнутой траектории/ Заряд из точки 1 перемещается по пути L1 в точку 2, а затем возвращается в исходное положение по другому пути L2. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:
. 
Работа этой силы на замкнутой траектории L = L1 + L2 равна нулю:
. 
Это уравнение, упростив, запишем так:
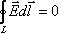. (3.18)
Разберём подробно последнее уравнение. Подынтегральное выражение — элементарная работа электрической силы, действующей на единичный положительный заряд, на перемещении 
здесь q = 1 — единичный заряд.
При подсчёте работы на замкнутой траектории необходимо сложить элементарные работы электрической силы на всех участках траектории. Иными словами, проинтегрировать (3.19) по замкнутому контуру L:
. 
(3.20)
Интеграл по замкнутому контуру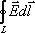 
= 
называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.
Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю:
Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.
Интеграл 
- называется циркуляцией вектора напряженности. Т.о. теорема о циркуляции: циркуляция вектора напряженности электростатического поля равна нулю. Из теоремы о циркуляции следует, что силовые линии не могут быть замкнутыми: они начинаются и кончаются на зарядах или уходят в бесконечность. Физический смысл теоремы о циркуляции заключается в том, что электрическое поле - потенциально.
16. Потенциал и разность потенциалов электростатического поля. Эквипотенциальные поверхности.
Потенциал электростатического поля — отношение потенциальной энергии заряда в поле к этому заряду:
(1.9)
Выражается потенциал в вольтах: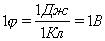 
Потенциал j не зависит от заряда q, помещенного в данную точку поля.
Для однородного поля 
потенциал зависит от напряженности E и от расстояния d от данной точки поля до нулевого потенциального уровня.
рис. 2
Работа поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность характеризует потенциал в данной точке поля созданного точечным зарядом Q смотри рис. 2.
(1.10),
где Q — заряд создающий поле, R — расстояние от данной точки поля до заряда Q.
Потенциальная энергия электрического взаимодействия системы n точечных зарядов qi равна
Wп = 1/2åqij i (1.14)
здесь j i — потенциал поля в точке, где находится заряд qi
Если поле создано двумя зарядами, то выполняется следствие принципа суперпозиции полей.
j = j 1 + j 2
Потенциал поля, созданного несколькими заряженными телами, равен алгебраической сумме потенциалов отдельных полей, создаваемых в данной точке пространства каждым из заряженных тел:
Разность потенциалов
A = - (W2 - W1) = - (j 2 - j 1)q = - D j q,
A = q0U (1.15)
Разность потенциалов характеризует работу поля по перемещению единичного положительного заряда (1 Кл) из начальной точки в конечную.
рис 4
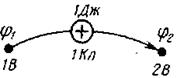
рис. 5 Единица разности потенциалов
ЭКВИПОТЕНЦИА́ЛЬНАЯ ПОВЕ́РХНОСТЬ, поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значение j= const. На плоскости эти поверхности представляют собой эквипотенциальные линии поля. Используются для графического изображения распределения потенциала.
Эквипотенциальные поверхности замкнуты и не пересекаются. Изображение эквипотенциальных поверхностей осуществляют таким образом, чтобы разности потенциалов между соседними эквипотенциальными поверхностями были одинаковы. В этом случае в тех участках, где линии эквипотенциальных поверхностей расположены гуще, больше напряженность поля.
Между двумя любыми точками на эквипотенциальной поверхности разность потенциалов равна нулю. Это означает, что вектор силы в любой точке траектории движения заряда по эквипотенциальной поверхности перпендикулярен вектору скорости. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности. Другими словами: эквипотенциальная поверхность ортогональна к силовым линиям поля, а вектор напряженности электрического поля Е всегда перпендикулярен эквипотенциальным поверхностям и всегда направлен в сторону убывания потенциала. Работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю, так как?j = 0.
Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд. Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности. Поверхность проводника в электростатическом поле является эквипотенциальной поверхностью.
17. Потенциал электростатического поля точечного заряда.
Тело, которое находится в потенциальном поле сил (а электростатическое поле, как уже известно, является потенциальным), обладает потенциальной энергией, за счет которой силы поля совершают работу. Как известно из классической механики, работа консервативных сил совершается за счет убыли потенциальной энергии. Значит работу сил электростатического поля можно считать как разность потенциальных энергий, которыми обладает точечный электрический заряд Q0 в начальной и конечной точках поля заряда Q:
(1)
откуда мы видим, что потенциальная энергия заряда Q0 в поле заряда Q равна
Она, как и в классической механике, определяется неоднозначно, а с точностью до произвольной постоянной С. Если считать, что при перенесении заряда в бесконечность (r→∞) потенциальная энергия обращается в нуль (U=0), то С=0 и потенциальная энергия заряда Q0, который находится в поле заряда Q на расстоянии r от него, равна
(2)
Для зарядов одинакового знака Q0Q>0 потенциальная энергия их взаимодействия (в данном случае - отталкивания) положительна, для разноименных зарядов Q0Q<0 и потенциальная энергия их взаимодействия (в данном случае - притяжения) отрицательна.
Если поле создается системой n точечных электрических зарядов Q1, Q2,..., Qn, то работа электростатических сил, которая совершается над зарядом Q0, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q0, который находится в этом поле, равна сумме потенциальных энергий Ui, каждого из зарядов:
(3)
Из формул (2) и (3) следует, что отношение U/Q0 не зависит от Q0 и является поэтому энергетической характеристикой электростатического поля, которая называется потенциалом:
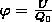(4)
Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.
Из формул (4) и (2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен
(5)
Работа, которую совершают силы электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 (см. (1), (4), (5)), может быть выражена как
(6)
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, которая совершается силами поля, при перемещении единичного положительного электрического заряда из точки 1 в точку 2.
Работа сил поля при перемещении заряда Q0 из точки 1 в точку 2 может быть выражена как
(7)
Приравняв (6) и (7), придем к формуле для разности потенциалов:
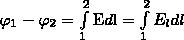(8)
где интегрирование можно производить вдоль любой линии, которая соединяет начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.
Если перемещать заряд Q0 из произвольной точки за далеко пределы поля, т. е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (6), A∞=Q0φ, откуда
(9)
Значит, потенциал — физическая величина, которая определяется работой по перемещению единичного положительного электрического заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, которую совершают внешние силы (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.
Из выражения (4) видно, что единица потенциала — вольт (В): 1 В равен потенциалу такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная ранее единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Н•м/(Кл•м)=1 Дж/(Кл•м)=1 В/м.
Из формул (3) и (4) следует, что если поле создается несколькими зарядами, то потенциал данного поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов: 
18. Связь напряженности и потенциала электростатического поля.
Будем искать, каким образом связаны напряженность электростатического поля, которая является его силовой характеристикой, и потенциал, который есть его энергетическая характеристика поля.
Работа по перемещению единичного точечного положительного электрического заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены достаточно близко друг к другу и x2—x1=dx, равна Exdx. Та же работа равна φ1—φ2=dφ. Приравняв обе формулы, запишем
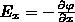(1)
где символ частной производной подчеркивает, что дифференцирование осуществляется только по х. Повторив эти рассуждения для осей у и z, найдем вектор Е:
где i, j, k — единичные векторы координатных осей х, у, z.
Из определения градиента следует, что
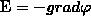или 
(2)
т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус говорит о том, что вектор напряженности Е поля направлен в сторону уменьшения потенциала.
19. Потенциал электростатического поля системы зарядов. Принцип суперпозиции. Потенциал поля точечного диполя.
Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Qi (i = 1, 2,..., n). Энергия взаимодействия всех n зарядов определится соотношением
, 
где rij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.
Принцип суперпозиции. Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q1, Q2¼, Qn имеем
, 
где ri - расстояние от точки поля, обладающей потенциалом j, до заряда Qi. Если заряд произвольным образом распределен в пространстве, то
, 
где r - расстояние от элементарного объема dx, dy, dz до точки (x, y, z), где определяется потенциал; V - объем пространства, в котором распределен заряд.
Рассчитаем значение потенциала электростатического поля в точке наблюдения 
в предположении, что потенциал бесконечно удаленной точки пространства равен нулю и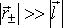 
. Ниже под величинами 
будем понимать модули соответствующих векторов. Точное выражение для потенциала в точке 
имеет вид:
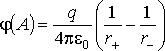. (2.2)
Векторы 
и 
связанны между собой зависимостью
, 
20. Потенциал и разность потенциалов электростатического поля бесконечной равномерно заряженной плоскости.
