Для непосредственного сложения синусоидальных функций необходимо производить достаточно громоздкие операции. Существенное упрощение достигается, если синусоидальную функцию изобразить в виде вращающегося вектора.
Векторное изображение синусоиды строится следующим образом (см. рис. 3.2).
 |
Рис. 3.2.
На плоскости из начала координат под углом 
, равному начальной фазе синусоиды, проводится прямая и на ней откладывается в масштабе отрезок, равный амплитуде колебания. Угол откладывается против часовой стрелки от горизонтальной оси, если 
; и по часовой стрелке, если 
. Если угол откладывать от горизонтальной оси, то проекция вектора на вертикальную ось равна (в выбранном масштабе) мгновенному значению синусоидальной функции.
Построим векторное изображение суммы двух функций (рис. 3.3):
(3.5)
Очевидно, что вместо сложения синусоид удобно геометрически складывать их векторные изображения. Таким образом, получили простейшую векторную диаграмму.
 |
Рис. 3.3.
Векторная диаграмма представляет собой совокупность векторов, изображающих синусоидальные функции одинаковой частоты, построенных с соблюдением масштаба и правильной ориентации их друг относительно друга по фазе.
Условились: вместо амплитуд на векторных диаграммах откладывать действующее значение функции.
Мгновенная мощность PR = uRi содержит две составляющие: постоянную и переменную, которая изменяется по закону косинуса с частотой 
(3.8)
Среднее за период значение мгновенной мощности (называется активной мощностью) равно:
Билет №10. Символическое изображение гармонических колебаний комплексным числом. Связь мгновенных значений колебаний с комплексной амплитудой.
Соотношения между амплитудами и начальными фазами гармонических токов и напряжений в пассивных элементах.
Любую гармоническую функцию 
можно изобразить в виде вектора (рис. 4.1, а), а каждому вектору можно поставить в соответствие комплексное число (рис. 4.1, б).
a)
 |
б)
Рис. 4.1.
Существуют три формы записи комплексного числа
1. 
- показательная (А - модуль комплексного числа, j - его аргумент);
2. 
- тригонометрическая;
3. 
- алгебраическая (а - вещественная часть, б - мнимая
часть).
Переход от одной формы записи к другой можно осуществить с помощью формул:
; 
; (4.1)
; 
.
Необходимо запомнить:
; 
; 
; 
. (4.2)
Комплексной амплитудой 
называется комплексная величина, модуль которой равен амплитуде синусоидального тока, а аргумент - начальной фазе.
В 
раз меньшую величину называют комплексным действующим
значением - комплексным током.
Аналогично
- комплексная амплитуда напряжения;
- комплексное напряжение.
Составим новое комплексное число
|
|
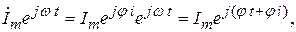
которое называется вращающимся вектором тока.
Разложим 
по формуле Эйлера:
(4.5)
Следовательно, синусоидальный ток является мнимой частью вращающегося вектора, т.е.
,
где j - знак мнимой части.
Часто величины i, u, называют оригиналами, а 
– их комплексными изображениями.
Билет №11. Закон Ома для комплексных амплитуд колебаний. Модуль и аргумент, вещественная и мнимая составляющие комплексного сопротивления и комплексной проводимости двухполюсника. Соотношения между комплексными амплитудами тока и напряжения в пассивных элементах.
Комплексным сопротивлением называется отношение комплексного напряжения 
к комплексному току 
:
(4.9)
Используя формулу Эйлера, получим
(4.10)
где 
- модуль комплексного сопротивления, равный полному сопротивлению цепи;
- аргумент комплексного сопротивления;
R и Х - активное и реактивное сопротивление цепи.
Комплексной проводимостью называется величина, обратная комплексному сопротивлению
; (4.11)
; 
;
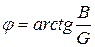Y, G, В - полная, активная, реактивная проводимость.
Очевидна следующая связь 
, используя которую можно установить зависимость между эквивалентными сопротивлениями и проводимостями ЭЦ. При заданном комплексном сопротивлении некоторого участка цепи можно определить комплексную проводимость того же участка:
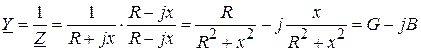(4.12)
Если задана комплексная проводимость некоторого участка ЭЦ, то комплексное сопротивление того же участка равно
. (4.13)
