Со знаком «+» в уравнение по МУН записывается узловое напряжение того узла, относительно которого составляется уравнение, все остальные – со знаком «-».
Задающие токи источников ЭДС и тока берутся со знаком «+», если направление источников ориентированно к узлу, относительно которого составляется уравнение, и со знаком «-» - если от узла.
При наличии в схеме ветви с идеальным источником ЭДС необходимо принять за опорный узел один из узлов к которому присоединена данная ветвь. Тогда узловое напряжение другого узла будет равным величине ЭДС.
Порядок расчета по МУН
1. Определяется число уравнений;
2. Выбирается опорный узел;
3. Составляется и решается система уравнений по МУН;
4. По закону Ома определяются токи ветвей.
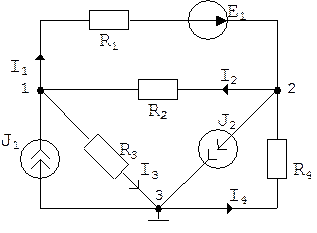Пример: Для цепи рис 2.8 составить уравнения по МУН и определить токи ветвей.
Рис. 2.8
Решение:
Примем U3 = 0;
 |
Токи ветвей определяются по закону Ома через найденные значения узловых напряжений:
Билет №8. Метод эквивалентного генератора.
Метод эквивалентного генератора основан на теореме об эквивалентном источнике (теорема Тевенена) – активном двухполюснике.
Теорема Тевенена для линейных электрических цепей утверждает, что любая электрическая цепь, имеющая два вывода и состоящая из комбинации источников напряжения, источников тока и резисторов (сопротивлений), с электрической точки зрения эквивалентна цепи с одним источником напряжения E и одним резистором R, соединенными последовательно.
В методе эквивалентного генератора (метод эквивалентного источника ЭДС) сложную разветвленную схему рассматривают как активный двухполюсник по отношению к ветви R с искомым током I, который определяют по выражению
I = EЭГ / (RЭГ + R),
где
EЭГ = Uхх – ЭДС эквивалентного генератора равная напряжению холостого хода между зажимами подключенного пассивного элемента R в ветви с искомым током;
RЭГ = Rвх – сопротивление эквивалентного генератора равное входному сопротивлению пассивного двухполюсника относительно разомкнутых зажимов.
Алгоритм метода эквивалентного генератора (метод эквивалентного источника ЭДС)
1. Определяют напряжение холостого хода Uхх. Для этого ветвь с искомым током разрывают, удаляя сопротивление, и оставляют ЭДС в этой ветви, если она имеется.
2. Задаются направлением токов в ветвях оставшейся схемы после размыкания ветви. Записывают выражение для напряжения Uхх между разомкнутыми зажимами по второму закону Кирхгофа. В это уравнение войдет ЭДС разомкнутой ветви.
3. Рациональным методом рассчитываются токи в схеме, вошедшие в выражение напряжения Uхх.
4. Определяют входное сопротивление двухполюсника относительно разомкнутых зажимов.
5. В соответствии с методом эквивалентного генератора (метод эквивалентного источника ЭДС), определяют искомый ток ветви.
Билет №9. Гармонические напряжения и токи, их параметры, векторное представление.
Действующие значения, мгновенная и средняя мощности гармонических колебаний.
Периодический процесс называется гармоническим, если функция f(t) (напряжение, ЭДС, ток) изменяется по закону синуса
f(t) = Am sin(wt +j); (3.1)
u = Um sin(wt +jU); e = Em sin(wt + je); i = Im sin(wt = ji)
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем
 ,
| (1) |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
 ,
| (2) |
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i - мгновенное значение тока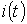 
;
u – мгновенное значение напряжения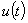 
;
е - мгновенное значение ЭДС 
;
р - мгновенное значение мощности 
.
Наибольшее по абсолютному значению отклонение колеблющейся величины называется ее амплитудой 
.
Наименьшее значение времени, после которого процесс полностью повторяется, называется периодом колебания Т.
Число циклов колебаний в единицу времени называется циклической частотой 
.
Число циклов колебаний в интервале времени равному 2p единицам, называется угловой частотой 
.
Величина 
называется фазой колебания. Она характеризует состояние колебания в любой момент времени t.
Значение фазы колебания в момент времени t=0 называется начальной фазой 
. Начальная фаза является алгебраической величиной. При 
начало синусоиды сдвинуто влево, а при 
- вправо от начала координат.
Действующим значением любой периодической функции называют ее среднеквадратичное значение за период.
. (3.2)
Действующее значение синусоидального тока или напряжения в 
раз меньше его амплитуды
(3.3)
Действующее значение периодического синусоидального тока равно по величине такому постоянному току, который, проходя через сопротивление R за интервал времени Т, выделит такое же количество тепла, что и данный периодический ток
(3.4)
Большинство измерительных приборов показывают действующее значение тока и напряжения
