Домашняя контрольная работа

Каждая задача содержит 10 вариантов. Студент выполняет тот вариант задачи, который соответствует номеру фамилии студента в списке академической группы, упорядоченного в алфавитном порядке, за вычетом числа кратного 10, если номер фамилии больше 10.

 

Условие каждой задачи необходимо переписать. Решение задачи сопровождать подробными пояснениями и ссылками на используемые определения, свойства, теоремы.

 

 

1. С помощью законов алгебры множеств и, используя равенство , докажите тождества:

1.1. ;

1.2. ;

1.3. ;

1.4. ;

1.5. ;

1.6. ;

1.7. ;

1.8. ;

1.9. ;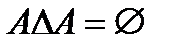

1.10. .

 

2. Запишите 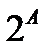перечислением для множеств:

2.1.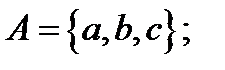

2.2.

2.3.

2.4.

2.5. ;

2.6. ;

2.7. ;

2.8. ;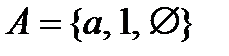

2.9. ;

2.10. .

 

3. Показать, что множество R является отношением эквивалентности на множестве . Найти все классы эквивалентности множества A по данному отношению R. Изобразить R в виде направленного графа:

3.1. ;

3.2.

;

3.3. ;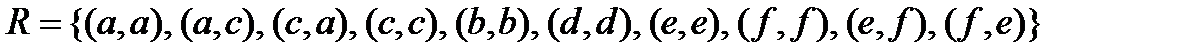

3.4. ;

3.5. ;

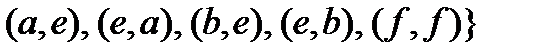3.6. ;

3.7.

;

3.8. ;

3.9. ;

3.10. .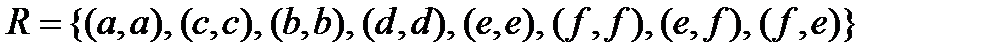

 

4. Нарисовать диаграмму Хассе, указать минимальные и максимальные элементы и наибольшие и наименьшие элементы, если последние существуют, следующих упорядоченных множеств (X, R):

№	X	R
4.1
4.2
4.3
4.4
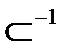
4.5	{3, 5, 7, 9, 15, 27, 33}	{(x, y)Î X 2| x — делитель y }
4.6	{3, 5, 7, 9, 15, 27, 33}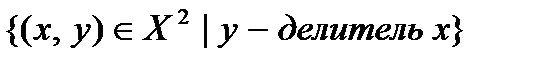
4.7	{3, 5, 7, 9, 15, 27, 35, 45}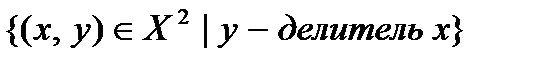
4.8	{3, 5, 7, 9, 15, 27, 35, 45}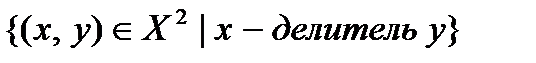
4.9	{3, 6, 9, 12, 15, 27, 36, 45}
4.10	{3, 6, 9, 12, 15, 27, 36, 45}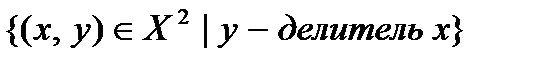

 

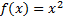5. Пусть : R®R задана формулой: . Найти и , если:

	C	D
5.1	[2, 3]	[-4, 4]
5.2	[-2, 3]	[0, 4]
5.3	[-4, 4]	[-4, 0]
5.4	{-4, 4}	[-4, 4]
5.5	[-4, 0]	[-4, 9]
5.6	[0, 4]	[-9, 4]
5.7	[-4, -1]	[-2, 4]
5.8	[-9, 4]	[-14, 4]
5.9	[4, 9]	[-14, -4]
5.10	[-1, 4]	[-45, 4]

 

 

6. Бинарная операция * определена на множестве X таблицей Кейли. Проверить ассоциативность этой операции. Будет ли (X, *) полугруппой, моноидом группой?

 

6.1. * a b c a a a a b b b b c c c c	6.2. * a b c a a b c b a b c c a b c	6.3. * a b c a a b c b b c a c c a b
6.4. * a b c a a a a b a b c c a c b	6.5. * a b c a a b c b b a c c c c a	6.6. * a b c a a a a b a a a c a a a
6.7. * a b c a a b c b b c c c c c c	6.8. * a b c a a a a b b c b c c c c	6.9. * a b c a a a a b b b b c c b c
6.10. * a b c a a a b b b c c c c b b

 

7. Следующие формулы с помощью равносильных преобразований привести к СДНФ и к СКНФ, если это возможно:

7.1. ;

7.2. ;

7.3. ;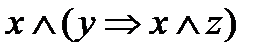

7.4. ;

7.5. ;

7.6. ;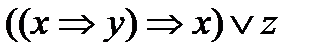

7.7. ;

7.8. ;

7.9. ;

7.10. .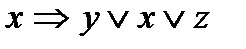

 

8. Является ли множество булевых функций { f ₁, f ₂} полным?

8.1 x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1     8.5 x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1     8.9 x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

8.2. x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1     8.6. x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1     8.10. x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

8.3. x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1     8.7. x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

8.4. x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1     8.8. x 1 x 2 x 3 f 1 f 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

 

.

9. Для орграфа, заданного матрицей длин дуг C = (c_ij), используя алгоритм Дейкстры найти кратчайший путь между вершинами s и t. Нарисовать диаграмму соответствующего орграфа.

Здесь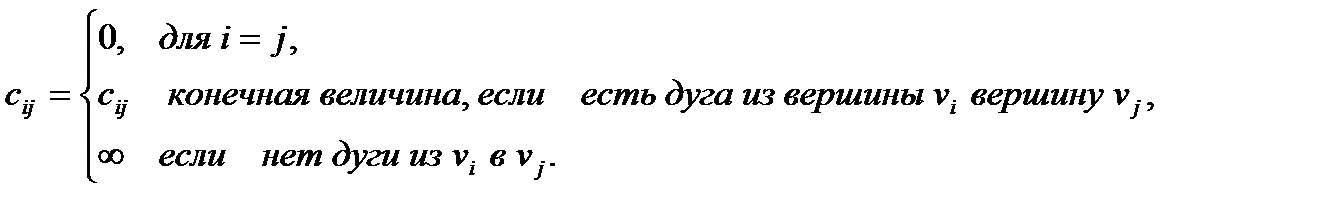

 

 

№
s	v 1	v 1	v 10	v 10	v 2	v 2	v 4	v 4	v 8	v 6
t	v 7	v 9	v 7	v 5	v 10	v 9	v 8	v 6	v 4	v 4

 

 

10. Найти максимальный поток в сети, заданной матрицей C = (c_ij), пропускных способностей дуг, где

10.1.

 

10.2.

 

10.3.

 

10.4.

 

10.5.

 

10.6.

 

10.7.

 

 

10.8.

 

 

10.9.

 

10.10.

 

 

11. Решить предложенные задачи из нижеследующего списка.

 

№ варианта
задачи	1, 11, 25, 39	2, 12, 26, 40	3, 13, 27, 41	4, 14, 28, 42	5, 15, 29, 43	6, 16, 30, 44	7, 17, 31, 45	8, 18, 32, 46	9, 19, 33, 47	10, 16, 34, 48

 

1. Найдите множества А и В такие, что и

2. Найдите множества А, В, С такие, что , .

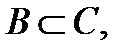
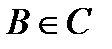3. Докажите и

4. Докажите и

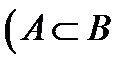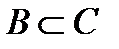5. Докажите и и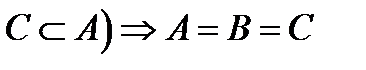

6. Если то следует, что ?

7. Доказать, что для произвольных множеств А, В, X, Y справедливы равенства

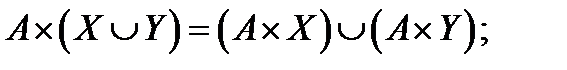
8. На множестве 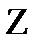заданы отношения: , . Исследуйте свойства отношений и . Постройте отношения , .

9. Исследуйте свойства отношения , заданного на бинарной матрицей: . Определите его тип. Постройте разбиение 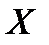, на классы, если есть отношение эквивалентности на .

10. Доказать, что два множества равны тогда и только тогда, когда результаты их пересечения и объединения совпадают.

11. Доказать, что если отношения и 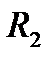рефлексивны, то рефлексивны отношения , , , .

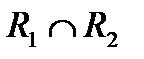12. Построить бинарное отношение:

a. рефлексивное, симметричное, но не транзитивное;

b. рефлексивное, антисимметричное, но не транзитивное;

c. рефлексивное, транзитивное, но не симметричное.

13. На множестве 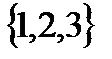построить все бинарные отношения, которые симметричны и антисимметричны одновременно.

14. Найдите число всевозможных антисимметричных бинарных отношений на множестве M, если |M|=n.

15. Докажите, что если 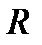- отношение эквивалентности на X, то тоже является отношением эквивалентности на X.

16. Докажите, что пересечение любого семейства отношений эквивалентности на множестве X является отношением эквивалентности на X.

17. Всегда ли объединение двух отношений эквивалентности на множестве X является отношением эквивалентности на X?

18. Отношение R из {1, 2, 3} в {Æ, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}} имеет следующую бинарную матрицу

 

 

Запишите R перечислением и определите словами или символом aRb.

19. Отношение R на множестве A={a, b, c, d, e} задано бинарной матрицей

 

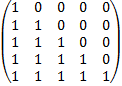а) б) c)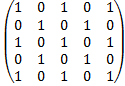

 

Составить список элементов R и нарисуйте направленный граф для R найдите, какие из них симметричные? Рефлексивные? Антисимметричные? Транзитивные?

20. Привести примеры бинарных отношений на A={1, 2, 3, 4}, которые являются функциями.

21. Задает все функции из A={1, 2, 3} с помощью стрелок. Какие из них являются инъекцией, сюръекциями, биекциями.

22. Какие из следующих подмножеств Z´Z являются функциями?

{(n, 2n) ï nÎ Z};

{ (2n, n) ï nÎ Z};

{ (n, n²) ï nÎ Z};

{ (n², n) ï nÎ Z};

23. Пусть A – множество всех прямых на плоскости. Какими свойствами обладают отношениями?

а) ;

б) .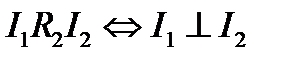

 

24. Пусть A – множество людей и .

Определите, какими свойствами обладает отношение R, если P(x,y) есть:

а) x является матерью для y;

б) x является братом для y;

в) x женат на y;

г) x не ниже, чем y.

 

25. Какими свойствами обладает отношение R на N, если:

а) n R m 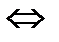n-m – кратно 3;

б) n R m n m для некоторого k N;

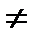в) n R m n m;

г) n R m m – делитель n?

 

26. Является ли операция вычитания на R ассоциативной? Коммутативной? Существует ли единичный элемент?

27. Как можно на основании таблицы Кэйли ответить на вопросы:

А) Является ли операция коммутативной?

Б) Существует ли единичный элемент?

28. Дана следующая таблица Кэйли для бинарной операции на X={a,b,c,d}. Показать, что не ассоциативна.

 

	a	b	c	d
a	a	b	c	d
b	b	d	a	a
c	c	a	b	d
d	d	a	b	c

 

29. Пусть X={a,b,c} и - коммутативная бинарная операция на Х такая, что а – единичный элемент и каждый элемент имеет обратный. Составьте таблицы Кэйли всех таких операций. Какие из них являются ассоциативными?

Будет ли коммутативной операцией на X=2^М ? Существует ли единичный элемент? Какие элементы имеют обратные?

30. Сколько различных бинарных операций может быть определено на множествах из двух, трех, четырех, n элементов?

31. Пусть - бинарная операция на Х. Известно, что существует единичный элемент и для любых x,y,z X выполняется равенство x (y z)=(x z) y. Покажите, что является коммутативной и ассоциативной операцией.

32. Покажите, что <2^M; > - группа.

33. Покажите, что множество всех квадратных матриц второго порядка является группой относительно операции сложения, а с операцией умножения матриц моноидом, но не группой. Покажите, что множество невырожденных матриц второго порядка с операцией умножения является группой.

34. Показать, что <R; max> - полугруппа, но не моноид.

35. Показать, что <[0,1]; min> - моноид, но не группа.

36. Построить таблицу истинности для булевых функций, реализованных формулами

А) Б) z => ( В) x => (y => )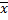

37. Какие из следующих формул равносильны?

А) x 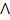y; Б) (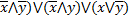; В) ; Г) .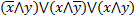

38. Является ли булевы функция f, заданная таблицей истинности, самодвойственной?

x	y	z	f

Проверить её принадлежность к классам T₀, T₁, T₄, T_≤, T_L. Является ли класс булевых функций, состоящий из одной этой функции полным?

 

 

39. Доказать, что в нетривиальном графе существуют вершины одинаковой степени.

40. Являются ли следующие графы изоморфными?

 

 

 

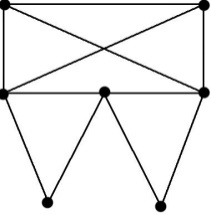
41. Доказать, что следующие графы являются изоморфными.

 

 

 

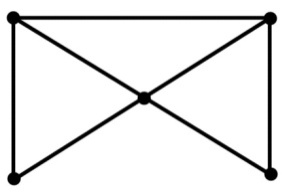
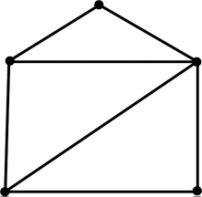
42. Доказать, что следующие числовые характеристики являются инвариантами графов:

p, q, k, δ(G)= , .

 

43. Нарисуйте все неизоморфные графы с 4 вершинами.

 

44. Нарисуйте все неизоморфные деревья с 4 вершинами.

 

45. Нарисуйте все неизоморфные ордеревья с 4 вершинами.

 

46. Построить орграф, матрицей смежности которого является следующая матрица:

 

 

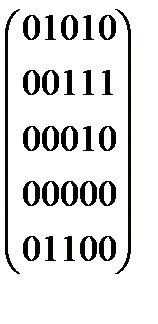
Является ли он сетью? Является ли он сильно связанным? Односторонне связанным? Найти его конденсацию.

 

47. Является ли следующий граф Петерсона двудольным? Эйлеровым? Гамильтоновым? Составить его матрицу смежности.

48. Число y(G)=|E|-|V|+ k называется цикломатическим числом графа G=<V,E>.

Доказать, что

А) Если является остовым подграфом графа G, то у(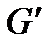)≤y(G);

Б) у(G)≥0 для всякого графа G;

В) у(G)=0 тогда и только тогда, когда граф G- ациклический.

 

49. Является ли группа <Z,+> конечно порожденной?

 

50. Доказать что в решетке из взаимного поглощения следует идемпотентность обеих операций.

 

51. Доказать, что в эйлеровом графе нет мостов.

52. Доказать, то граф связен ó, когда он имеет оcтовной подграф, являющийся деревом.

53. Доказать, что если δ(G)>(p-1)/2, то граф G связен, (δ(G)= ).

54. Как может изменится количество компонент сильной связности орграфа при добавлении к нему одной дуги?

55. Найти вершинную связность и реберную связность следующих графов

56. Напишите матрицу смежности и матрицу инциденций следующих графов

57. Нарисовать диаграмму графа по следующей матрице смежности