Блочные шифры. Общие сведения о блочных шифрах

 

Ответ:

В зависимости от наличия либо отсутствия ключа кодирующие алгоритмы делятся на тайнопись и криптографию. В зависимости от соответствия ключей шифрования и дешифрования – на симметричные и асимметричные. В зависимости от типа используемых преобразований – на подстановочные и перестановочные. В зависимости от размера шифруемого блока – на потоковые и блочные шифры.

Сама криптография не является высшей ступенью классификации смежных с ней дисциплин. Наоборот, криптография совместно с криптоанализом (целью которого является противостояние методам криптографии) составляют комплексную науку – криптологию.

Необходимо отметить, что в русскоязычных текстах по данному предмету встречаются различные употребления основных терминов, таких как "криптография", "тайнопись" и некоторых других. Более того, и по классификации криптоалгоритмов можно встретить различные мнения. В связи с этим автор не претендует на то, что его вариант использования подобных терминов является единственно верным.

В отношении криптоалгоритмов существует несколько схем классификации, каждая из которых основана на группе характерных признаков. Таким образом, один и тот же алгоритм "проходит" сразу по нескольким схемам, оказываясь в каждой из них в какой-либо из подгрупп.

Основной схемой классификации всех криптоалгоритмов является следующая:

3. Тайнопись.
Отправитель и получатель производят над сообщением преобразования, известные только им двоим. Сторонним лицам неизвестен сам алгоритм шифрования. Некоторые специалисты считают, что тайнопись не является криптографией вообще, и автор находит это совершенно справедливым.

4. Криптография с ключом.
Алгоритм воздействия на передаваемые данные известен всем сторонним лицам, но он зависит от некоторого параметра – "ключа", которым обладают только отправитель и получатель.

1. Симметричные криптоалгоритмы.
Для зашифровки и расшифровки сообщения используется один и тот же блок информации (ключ).

2. Асимметричные криптоалгоритмы.
Алгоритм таков, что для зашифровки сообщения используется один ("открытый") ключ, известный всем желающим, а для расшифровки – другой ("закрытый"), существующий только у получателя.

Весь дальнейший материал будет посвящен криптографии с ключом, так как большинство специалистов именно по отношению к этим криптоалгоритмам используют термин криптография, что вполне оправдано. Так, например, любой криптоалгоритм с ключом можно превратить в тайнопись, просто "зашив" в исходном коде программы некоторый фиксированный ключ. Обратное же преобразование практически невозможно.

В зависимости от характера воздействий, производимых над данными, алгоритмы подразделяются на:

3. Перестановочные
Блоки информации (байты, биты, более крупные единицы) не изменяются сами по себе, но изменяется их порядок следования, что делает информацию недоступной стороннему наблюдателю.

4. Подстановочные
Сами блоки информации изменяются по законам криптоалгоритма. Подавляющее большинство современных алгоритмов принадлежит этой группе.

Заметьте: любые криптографические преобразования не увеличивают объем информации, а лишь изменяют ее представление. Поэтому, если программа шифрования значительно (более, чем на длину заголовка) увеличивает объем выходного файла, то в ее основе лежит неоптимальный, а возможно и вообще некорректный криптоалгоритм. Уменьшение объема закодированного файла возможно только при наличии встроенного алгоритма архивации в криптосистеме и при условии сжимаемости информации (так, например, архивы, музыкальные файлы формата MP3, видеоизображения формата JPEG сжиматься более чем на 2-4% не будут).

В зависимости от размера блока информации криптоалгоритмы делятся на:

3. Потоковые шифры.
Единицей кодирования является один бит. Результат кодирования не зависит от прошедшего ранее входного потока. Схема применяется в системах передачи потоков информации, то есть в тех случаях, когда передача информации начинается и заканчивается в произвольные моменты времени и может случайно прерываться. Наиболее распространенными предствателями поточных шифров являются скремблеры.

4. Блочные шифры
Единицей кодирования является блок из нескольких байтов (в настоящее время 4-32). Результат кодирования зависит от всех исходных байтов этого блока. Схема применяется при пакетной передаче информации и кодировании файлов.

 

Сеть Фейштеля

Ответ:

Сетью Фейштеля называется метод обратимых преобразований текста, при котором значение, вычисленное от одной из частей текста, накладывается на другие части. Часто структура сети выполняется таким образом, что для шифрования и дешифрования используется один и тот же алгоритм – различие состоит только в порядке использования материала ключа.

Сеть Фейштеля является дальнейшей модификацией описанного выше метода смешивания текущей части шифруемого блока с результатом некоторой функции, вычисленной от другой независимой части того же блока. Эта методика получила широкое распространение, поскольку обеспечивает выполнение требования о многократном использовании ключа и материала исходного блока информации.

Классическая сеть Фейштеля имеет следующую структуру:

Рис.1.

Независимые потоки информации, порожденные из исходного блока, называются ветвями сети. В классической схеме их две. Величины Vi именуются параметрами сети, обычно это функции от материала ключа. Функция F называется образующей. Действие, состоящее из однократного вычисления образующей функции и последующего наложения ее результата на другую ветвь с обменом их местами, называется циклом или раундом (англ. round) сети Фейштеля. Оптимальное число раундов K – от 8 до 32. Важно то, что увеличение количества раундов значительно увеличивает криптоскойстость любого блочного шифра к криптоанализу. Возможно, эта особенность и повлияла на столь активное распространение сети Фейштеля – ведь при обнаружении, скажем, какого-либо слабого места в алгоритме, почти всегда достаточно увеличить количество раундов на 4-8, не переписывая сам алгоритм. Часто количество раундов не фиксируется разработчиками алгоритма, а лишь указываются разумные пределы (обязательно нижний, и не всегда – верхний) этого параметра.

Сразу же возникает вопрос, – является ли данная схема обратимой? Очевидно, да. Сеть Фейштеля обладает тем свойством, что даже если в качестве образующей функции F будет использовано необратимое преобразование, то и в этом случае вся цепочка будет восстановима. Это происходит вследствие того, что для обратного преобразования сети Фейштеля не нужно вычислять функцию F-1.

Более того, как нетрудно заметить, сеть Фейштеля симметрична. Использование операции XOR, обратимой своим же повтором, и инверсия последнего обмена ветвей делают возможным раскодирование блока той же сетью Фейштеля, но с инверсным порядком параметров Vi. Заметим, что для обратимости сети Фейштеля не имеет значение является ли число раундов четным или нечетным числом. В большинстве реализаций схемы, в которых оба вышеперечисленные условия (операция XOR и уничтожение последнего обмена) сохранены, прямое и обратное преобразования производятся одной и той же процедурой, которой в качестве параметра передается вектор величин Vi либо в исходном, либо в инверсном порядке.

С незначительными доработками сеть Фейштеля можно сделать и абсолютно симметричной, то есть выполняющей функции шифрования и дешифрования одним и тем же набором операций. Математическим языком это записывается как "Функция EnCrypt тождественно равна функции DeCrypt". Если мы рассмотрим граф состояний криптоалгоритма, на котором точками отмечены блоки входной и выходной информации, то при каком-то фиксированном ключе для классической сети Фейштеля мы будем иметь картину, изображенную на рис.2а, а во втором случае каждая пара точек получит уникальную связь, как изображено на рис. 2б. Модификация сети Фейштеля, обладающая подобными свойствами приведена на рисунке 3. Как видим, основная ее хитрость в повторном использовании данных ключа в обратном порядке во второй половине цикла. Необходимо заметить, однако, что именно из-за этой недостаточно исследованной специфики такой схемы (то есть потенциальной возможности ослабления зашифрованного текста обратными преобразованиями) ее используют в криптоалгоритмах с большой осторожностью.

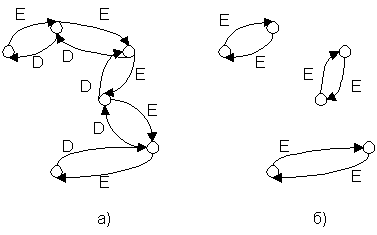
Рис.2.

 

А вот модификацию сети Фейштеля для большего числа ветвей применяют гораздо чаще. Это в первую очередь связано с тем, что при больших размерах кодируемых блоков (128 и более бит) становится неудобно работать с математическими функциями по модулю 64 и выше. Как известно, основные единицы информации обрабатываемые процессорами на сегодняшний день – это байт и двойное машинное слово 32 бита. Поэтому все чаще и чаще в блочных криптоалгоритмах встречается сеть Фейштеля с 4-мя ветвями. Самый простой принцип ее модификации изображен на рисунке 4а. Для более быстрого перемешивания информации между ветвями (а это основная проблема сети Фейштеля с большим количеством ветвей) применяются две модифицированные схемы, называемые "type-2" и "type-3". Они изображены на рисунках 4б и 4в.

Сеть Фейштеля надежно зарекомендовала себя как криптостойкая схема произведения преобразований, и ее можно найти практически в любом современном блочном шифре. Незначительные модификации касаются обычно дополнительных начальных и оконечных преобразований (англоязычный термин – whitening) над шифруемым блоком. Подобные преобразования, выполняемые обычно также либо "исключающим ИЛИ" или сложением имеют целью повысить начальную рандомизацию входного текста. Таким образом, криптостойкость блочного шифра, использующего сеть Фейштеля, определяется на 95% функцией F и правилом вычисления Vi из ключа. Эти функции и являются объектом все новых и новых исследований специалистов в области криптографии.

 

Рис.3.

Рис.4.

 

9. AES: cтандарт блочных шифров США c 2000 года. Общие сведения о конкурсе AES

Ответ:

В 1998 году был объявлен открытый конкурс на криптостандарт США на несколько первых десятилетий XXI века. Победителем конкурса был признан бельгийский блочный шифр Rijndael. Скорее всего он станет стандартом де-факто блочного шифрования во всем мире.

В 80-х годах в США был принят стандарт симметричного криптоалгоритма для внутреннего применения DES (Data Encryption Standard), который получил достаточно широкое распространение в свое время. Однако на текущий момент этот стандарт полностью неприемлем для использования по двум причинам: 1) основной – длина его ключа составляет 56 бит, что чрезвычайно мало на современном этапе развития ЭВМ, 2) второстепенной – при разработке алгоритм был ориентирован на аппаратную реализацию, то есть содержал операции, выполняемые на микропроцессорах за неприемлимо большое время (например, такие как перестановка бит внутри машинного слова по определенной схеме).

Все это сподвигло Американский институт стандартизации NIST – National Institute of Standards & Technology на объявление в 1997 году конкурса на новый стандарт симметричного криптоалгоритма. На сей раз уже были учтены основные промахи шифра-предшественника, а к разработке были подключены самые крупные центры по криптологии со всего мира. Тем самым, победитель этого соревнования, названного AES – Advanced Encryption Standard, станет де-факто мировым криптостандартом на ближайшие 10-20 лет.

Требования, предъявленные к кандидитам на AES в 1998 году, были предельно просты:

1. алгоритм должен быть симметричным,

2. алгоритм должен быть блочным шифром,

3. алгоритм должен иметь длину блока 128 бит, и поддерживать три длины ключа: 128, 192 и 256 бит.

Дополнительно кандидатам рекомендовалось:

1. использовать операции, легко реализуемые как аппаратно (в микрочипах), так и программно (на персональных компьютерах и серверах),

2. ориентироваться на 32-разрядные процессоры,

3. не усложнять без необходимости структуру шифра для того, чтобы все заинтересованные стороны были в состоянии самостоятельно провести независимый криптоанализ алгоритма и убедиться, что в нем не заложено каких-либо недокументированных возможностей.

На первом этапе в оргкомитет соревнования поступило 15 заявок из совершенно разных уголков мира. В течение 2 лет специалисты комитета, исследуя самостоятельно, и изучая публикации других исследователей, выбрали 5 лучших представителей, прошедших в "финал" соревнования.

Алгоритм	Создатель	Страна	Быстродействие (asm, 200МГц)
MARS	IBM	US	8 Мбайт/с
RC6	R.Rivest & Co	US	12 Мбайт/с
Rijndael	V.Rijmen & J.Daemen	BE	7 Мбайт/с
Serpent	Universities	IS, UK, NO	2 Мбайт/с
TwoFish	B.Schneier & Co	US	11 Мбайт/с

Все эти алгоритмы были признаны достаточно стойкими и успешно противостоящими всем широко известным методам криптоанализа.

2 октября 2000 года NIST объявил о своем выборе – победителем конкурса стал бельгийский алгоритм RIJNDAEL. С этого момента с алгоритма-победителя сняты все патентные ограничения – его можно будет использовать в любой криптопрограмме без отчисления каких-либо средств создателю.

10. Симметричные криптосистемы

Симметричные криптосистемы являются полноценными программами, которые могут на основе симметричных криптоалгоритмов кодировать и декодировать файлы произвольной длины. Криптосистемы устраняют целый класс "потенциальных уязвимостей" систем, использующих симметричные криптоалгоритмы.

Криптоалгоритмы несомненно являются "сердцем" криптографических систем, но, как мы сейчас увидим, их непосредственное применение без каких-либо модификаций для кодирования больших объемов данных на самом деле не очень приемлимо.

Все недостатки непосредственного применения криптоалгоритмов устраняются в криптосистемах. Криптосистема – это завершенная комплексная модель, способная производить двусторонние криптопреобразования над данными произвольного объема и подтверждать время отправки сообщения, обладающая механизмом преобразования паролей и ключей и системой транспортного кодирования. Таким образом, криптосистема выполняет три основные функции:

1. усиление защищенности данных,

2. облегчение работы с криптоалгоритмом со стороны человека

3. обеспечение совместимости потока данных с другим программным обеспечением.

Конкретная программная реализация криптосистемы называется криптопакетом.