Еще в ХVII в. заметили, что численность популяций растет по закону геометрической прогрессии, а уже в конце ХVIII в. Томас Мальтус (1766-1834) выдвинул свою известную теорию о росте народонаселения в геометрической прогрессии. Эта закономерность роста выражается кривой, изображенной на рис. 3.2, a.
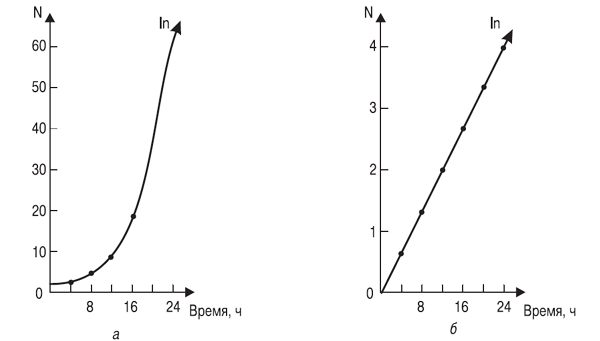
Рис. 3.2. Экспоненциальный рост гипотетической популяции
одноклеточного организма, делящегося каждые 4 часа:
а ¾ арифметическая шкала; б ¾ логарифмическая шкала
На современном математическом языке эта кривая (рис. 3.2) отражает экспоненциальный рост численности организмов и описывается уравнением:
Nt = N o ert,
где Nt ¾ численность популяции в момент времени t;
N o ¾ численность популяции в начальный момент времени t 0;
e ¾ основание натурального логарифма (2,7182);
r ¾ показатель, характеризующий темп размножения особей в данной популяции.
Экспоненциальный рост возможен только тогда, когда r имеет постоянное численное значение, так как скорость роста популяции пропорциональна самой численности:

Если численность отложить в логарифмическом масштабе, то кривая приобретает вид прямой линии (рис. 3.2, б).
Таким образом, экспоненциальный рост численности популяции ¾ это рост численности ее особей в неизменяющихся условиях.
Условия, сохраняющиеся длительное время постоянными, невозможны в природе. Если бы это было не так, то, например, обычные бактерии могли бы дать такую массу органического вещества, которая могла бы покрыть весь земной шар слоем толщиной в два метра за два часа.
Однако такого в природе не происходит, так как существует множество ограничивающих факторов. Но есть примеры, когда при замедлении роста, т. е. при снижении r, экспоненциальный рост сохраняется, может он возникать и на коротких отрезках жизни популяций.
Чтобы иметь полную картину динамики численности популяции, а также рассчитать скорость ее роста, необходимо знать величину так называемой чистой скорости воспроизводства (R о), которая показывает, во сколько раз увеличивается численность популяции за одно поколение, за время его жизни ¾ T,

где N т ¾ численность нового поколения;
N o ¾ численность особей предшествующего поколения;
R o ¾ чистая скорость воспроизводства, показывающая также, сколько вновь родившихся особей приходится на одну особь поколения родителей.
Если R o = 1, то популяция стационарная, ¾ численность ее сохраняется постоянной.
Скорость роста популяции обратно пропорциональна длительности поколения
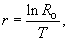
отсюда ясно, что чем раньше происходит размножение организмов, тем больше скорость роста популяции. Это в равной степени относится и к популяции человека, отсюда ¾ важность значения этой закономерности в демографической политике любого государства.
Воздействие экологических факторов на скорость роста популяции может довести численность популяции до стабильной (r = 0), либо ее уменьшить, т. е. экспоненциальный рост замедляется или останавливается полностью и J-образная кривая экспоненциального роста как бы останавливается и выполаживается, превращаясь в так называемую S-образную кривую (рис. 3.3, а).
В природе так и происходит: экспоненциальный рост наблюдается какое-то достаточно короткое время, после чего ограничивающие факторы его стабилизируют и дальнейшее развитие популяции идет по логистической модели, что и описывается S -образной, или логистической кривой роста популяции.

Рис. 3.3. Логистическая модель роста популяции:
а ¾ кривая роста численности (N); б ¾ зависимость удельной скорости роста (r) от численности (N); в ¾ зависимость рождаемости (b) и смертности (d) от численности; K ¾ предельная численность
В основе логистической модели (см. рис. 3.3) лежит простое допущение, что скорость роста популяции (rа) линейно снижается по мере роста численности вплоть до нуля при некой численности K. Итак, при начальной численности N о (близкой к нулю) скорость роста имеет максимальное значение ¾ r max, а при N = K, rа = 0. В результате решения уравнения логистической кривой получаем зависимость:
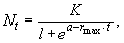
где Nt ¾ численность популяции в момент времени t;
e ¾ основание натурального логарифма;
a ¾ постоянная интегрирования.
Величину K называют еще емкостью среды в отношении особей данной популяции. Здесь речь идет о биологической емкости среды ¾ степени способности природного или природно-антропогенного окружения обеспечивать нормальную жизнедеятельность (дыхание, питание, размножение, отдых и т. п.) определенному числу организмов и их сообществ без заметного нарушения самого окружения (Реймерс, 1990).
Однако плато на S -образной кривой далеко не всегда бывает гладким, потому что колебания численности происходят постоянно, что отражается в виде колебаний кривой вокруг асимптоты «K» (рис. 3.4), эти колебания называются флуктуациями численности, которые могут быть сезонными и годовыми. Первые обусловлены абиотическими факторами, вторые ¾ плюс к этому, еще и внутренними, биотическими. Колебания, вызванные биотическими факторами, называют осцилляциями (рис. 3.5), они отличаются высокой регуляцией и их даже называют циклами. Многие факторы, природные и антропогенные, вызывающие флуктуации, в значительной мере можно учесть, введя в формулу поправочные коэффициенты. Такие формулы позволяют прогнозировать реальный рост популяции животных и подобные процессы в демографии людского населения.
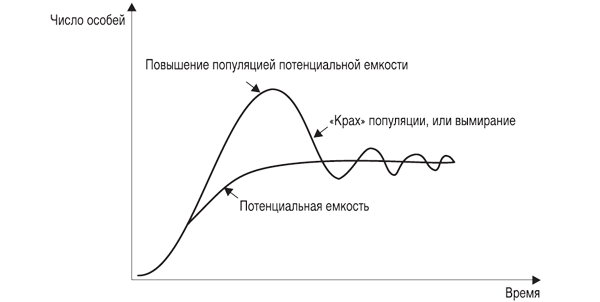
Рис. 3.4. Преобразование J-образной кривой роста численности в S-образную кривую
при ограничивающем воздействии лимитирующих факторов (по Т. Миллеру, 1993)
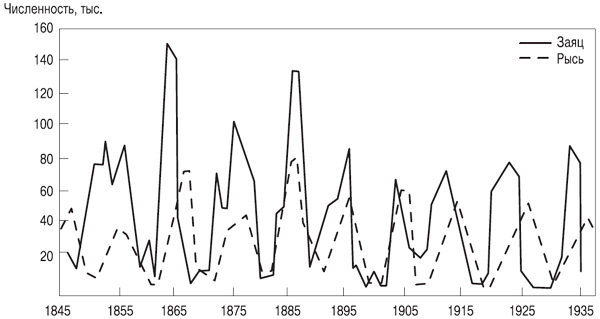
Рис. 3.5. Изменение численности рыси и зайца ¾ классический пример
цикличности колебаний популяций
В настоящее время уже достаточно моделей, подтверждающих логистическую модель, как на чисто природных объектах, так и на природно-антропогенных. Например, А. М. Гиляров (1990) приводит сведения о размножении северных оленей, интродуцированных (вселенных в местообитания, где они раньше не проживали) на острова Берингова моря. С небольших когорт, состоящих из нескольких десятков особей, в течение ряда лет рост численности по экспоненциальному закону приводил к возникновению популяции оленей, состоящей из нескольких тысяч голов. Затем наблюдалось резкое падение численности тоже до нескольких десятков голов за короткое время, один - три года. Причина ¾ полный расход пищевых ресурсов, которыми обладали эти острова.






