По определению:
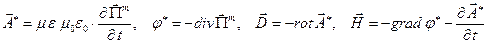
Рассмотрим уравнение
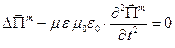
Уравнения () и () являются однородными, это свидетельствует о том, что источники векторных полей потенциалов Герца располагаются на границе области, в которой рассматривают соответствующее волновое уравнение.
Случай проводящей среды, материальные уравнения которой суть
,
а значения электрических и магнитных параметров среды постоянны, можно описать соотношениями:
,
где
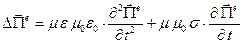
Комплексные силовые составляющие и потенциалы электромагнитного поля.
Среда изотропная, однородная и проводящая электрический ток. Потенциалы Зильберштейна и Бейтмана (начало ХХ века).
Введём обозначение;
Система уравнений Максвелла может быть сведена к двум уравнениям:
Повторное применение операции 
к первому из полученных уравнений и элементарные преобразования приводят к результату: 
Если в этом уравнении отделить друг от друга действительную и мнимую части, получим:
В этой форме записи уравнений электродинамики объёмные источники соответствующих векторных полей показаны явно (правые части уравнений).
Потенциалы Дебая.
Потенциалы Дебая оказываются эффективным средством решения векторного уравнения Гельмгольца, оно возникает при попытке решить волновое векторное уравнение в форме произведения амплитуды искомой функции на экспоненциальный сомножитель вида 
:
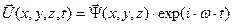
Волновое уравнение электромагнитного поля с учётом проводимости среды
Уравнение Гельмгольца:
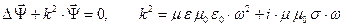
Волновой вектор - комплексная величина, векторное уравнение в декартовой системе координат приводит к уравнениям Гельмгольца для отдельных компонент вектора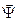 
:
Ниже можно рассматривать уравнение Гельмгольца для произвольной скалярной функции 
Рассмотрим следующие векторные поля
Следствия (свойства):
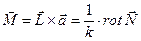
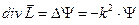
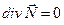
Часть этих свойств совершенно очевидна, а некоторые свойства можно доказать:
Рассмотрим
имеет место:
действительно:
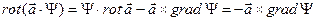
рассматриваемое свойство доказано
Произвольное векторное поле, удовлетворяющее уравнению Гельмгольца, в общем случае можно описать следующей зависимостью:
В заключение раздела заметим, что успех использования того или иного способа введения потенциалов электромагнитного поля зависит не только от вида системы дифференциальных уравнений электромагнитного поля в конкретной среде, но и от вида конкретных граничных условий для "силовых" векторов электромагнитного поля 
и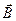 
,
которые должны быть выражены через введённые потенциалы электромагнитного поля.
