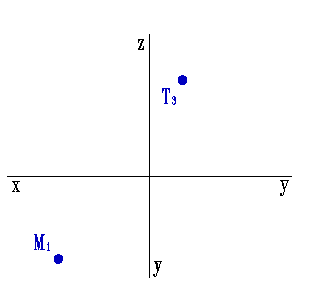
Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве (рис.17).

Рис. 17. Определение положения прямой по точке и углам наклона к плоскостям проекций
положение прямой линии относительно плоскостей проекций.
Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.18).
| ||||||||||||||||||||
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.19).
Для любой пары точек горизонтали должно быть справедливо равенство
zA=zB Þ A2B2//0x; A3B3//0y Þ xA - xB≠, yA–yB≠, zA–zB=.

| 
| ||
| а) модель | б) эпюр | ||
| Рис. 19. Горизонтальная прямая |
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями (рис.20).
yA=yBÞ A 1 B 1x, A 3 B 3z Þ xA–xB≠, yA–yB=, zA–zB≠.

| 
| ||
| а) модель | б) эпюр | ||
| Рис. 20. Фронтальная прямая |
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 21).
xA=xB Þ A 1 B 1y, A 2 B 2z Þ xA–xB=y, yA–yB≠, zA–zB≠.
Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.

| 
| ||
| а) модель | б) эпюр | ||
| Рис.21. Профильная прямая |
3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально проецирующая прямая - АВ (рис.22)
xA–xB= ü
yA–yB≠ý
zA–zB= þ,

| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 22. Фронтально проецирующая прямая |
3.2. Профильно проецирующая прямая - АВ (рис.23)
xА–xB≠ü
yА–yB=ý
zА–zB=þ,

| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 23. Профильно-проецирующая прямая |
3.3. Горизонтально проецирующая прямая - АВ (рис.24)
xА–xВ = ü
yА–yВ = ý
zА–zВ ≠ þ.

| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 24. Горизонтально-проецирующая прямая |
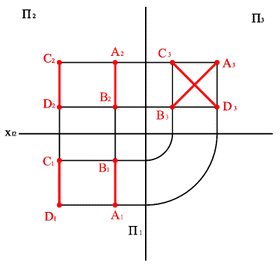
3. Прямые параллельные биссекторным плоскостям (рис. 25)
АВ S1 бис Þ xA – xB =; zB – zA = yB – yA;
СD S2 бис Þ xС – xD =; zD – zC = yC – yD.
Биссекторной плоскостью называется плоскость, проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П1 и П2 пополам.
Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (S1бис), а через 2 и 4 четверти - второй (S2бис).
4. Прямые перпендикулярные биссекторным плоскостям (рис. 25)
АВ S ^ 2бис Þ xA – xB =; zB – zA = yВ – yА;
СD S ^ 1бис Þ xС – xD =; zD – zC = yC–yD.

| 
| ||||||||||||

| 
| ||||||||||||
| а) модель б) эпюр | |||||||||||||
Рис. 25. Прямые параллельные и перпендикулярные биссекторным плоскостям
следы прямой линии
Следом прямой линии называется точка (рис. 26), в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её координат должна быть равна нулю).
Горизонтальный след - М (zM) = -точка пересечения прямой с горизонтальной плоскостью проекций.
Фронтальный след - N (yN) =- точка пересечения прямой с фронтальной плоскостью проекций.
Профильный след - Т (xТ) =- точка пересечения прямой с профильной плоскостью проекций.
Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N2ºN, а N1 лежит на оси x, N3 - на оси z. Отмеченные особенности в расположении следов проекций позволяет сформулировать следующие правила: |
Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью x и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой.
2. Для построения фронтального следа N прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.

Рис. 27. Нахождение горизонтального и фронтального следов прямой линии
С помощью этих правил найдены на эпюре следы прямой а (рис.27). Здесь же показаны совпавшие проекции точки А, принадлежащей рассматриваемой прямой. Особенность этой точки в том, что она равноудалена от плоскостей проекций, то есть находятся в биссекторной плоскости S2бис.
Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.
Взаимное расположение точки и прямой
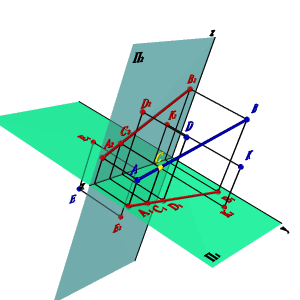
Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рис. 28 точек, только одна точка С лежит на прямой АВ.

| 
| ||
| а) эпюр | б) модель | ||
| Рис. 28. Взаимное расположение точки и прямой |
В тех случаях, когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П 1, П 2 и П 3), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П 1, П 2 или П 3. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций (рис.29).

| 
| ||
| а) эпюр | б) модель | ||
| Рисунок 29. Точка и прямая, расположенные в профильной плоскости уровня |
Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении.
Зная это условие можно определить принадлежность точки К прямой АВ:
А 2 К 2 / К 2 В 2 ¹ А 1 К 1/ К 1 В 1 Þ К Ï АВ
Тест "Проекции прямой"
| Проекция отрезка всегда меньше самого отрезка | Да | Нет |
| Отрезок прямой линии можно графически задать с помощью двух точек | Да | Нет |
| Отрезок прямой линии можно графически задать с помощью одной проекции | Да | Нет |
| Отрезок прямой линии можно графически задать с помощью точки и углов наклона к плоскостям проекций | Да | Нет |
| α - угол наклона прямой к горизонтальной плоскости проекций | Да | Нет |
Практикум по решению задач.
Тема: Проекции прямой линии
Задача 1.