Практикум по решению задач

Задача 1.

По двум центральным проекциям треугольника АВС определить его пространственное положение.

Задача 2.

По имеющимся параллельным проекциям четырехугольника АВСD построить пространственное положение четырехугольника АВСD и построить недостающую проекцию его вершины D.

Задача 3.

Построить тень дорожного знака, если известна тень одного столба.

Задача 4.

Построить проекцию параллелепипеда АВСDА^*В^*С^*D ^* на плоскость его основания по направлению диагонали А^*С.

Задача 5.

Построить тень, полученную при освещении сооружения двумя светильниками.

Проекции с числовыми отметками.

В проекциях с числовыми отметками плоскость проекций П _i называют плоскостью нулевого уровня и обозначают П ₀. Идея этого метода состоит в том, что на плоскость П ₀ ортогонально проецируют точку и вместе с проекцией точки задают ее расстояние до плоскости П ₀ (рис. 5). Это расстояние называют числовой отметкой точки и задают обычно в метрах. Числовую отметку точки пишут внизу справа от обозначения ее изображения.

Если плоскость нулевого уровня расположена горизонтально, то чертеж называют планом. На плане всегда указывают линейный масштаб и при необходимости дают ориентацию относительно сторон света.

Очень удобно в проекциях с числовыми отметками изображать линии уровня, все точки которых имеют одинаковые отметки. Линии уровня проецируются на П ₀ без искажения своей формы (применяется в картографии).

Проекции с числовыми отметками позволяют просто решать многие задачи. Обратимость чертежей в проекциях с числовыми отметками очевидна.

Зарождение идеи этого метода относят к средним векам. Уже тогда многие народы, пользующие картами с показаниями морских глубин, умели изображать точку при помощи ее проекции и отметки. Однако теоретическое обоснование метод получил лишь в 19 веке, благодаря французскому военному инженеру – капитану Нуазе (1823 г.).

Чертежи в проекциях с числовыми отметками построены на одной плоскости проекций – на одной картине и часто называются однокартинными.

Рис.5. Метод с числовыми отметками

метод монжа.

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем - крупным французским геометром конца 18, начала 19 веков, 1789-1818 гг. одним из основателей знаменитой политехнической школы в Париже и участником работ по введению метрической системы мер и весов.

Постепенно накопившиеся отдельные правила и приемы таких изображений были приведены в систему и развиты в труде Г. Монжа "Geometrie descriptive". Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.

В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.6). Одну из плоскостей проекций П ₁ располагают горизонтально, а вторую П ₂ - вертикально. П ₁ - горизонтальная плоскость проекций, П ₂ - фронтальная. Плоскости бесконечны и непрозрачны.

Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

Линия пересечения плоскостей проекций называется осью координат и обозначается x ₂₁.

Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти.

Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П ₁ совмещают вращением вокруг оси x ₁₂ с плоскостью П ₂ (рис.6).

Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром Монжа (франц. Epure – чертеж.) или комплексным чертежом.

Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы).

Рассмотрим способы их образования, графического задания и возможные варианты положения по отношению к плоскостям проекций.

Рис.6. Пространственная модель двух плоскостей проекций

Точка.

Точка.

Точка в ортогональной системе двух плоскостей проекций.

Точка в ортогональной системе трех плоскостей проекций.

Положение точек относительно плоскостей проекций.

Взаимное расположение точек.

Геометрический объект любой сложности можно рассматривать как геометрическое место точек, по взаимному расположению, которых можно составить представление об объекте, а по расположению их относительно системы координат можно судить о положении его в пространстве.

Точка - одно из основных понятий геометрии. При систематическом изложении геометрии точка обычно принимается за одно из исходных понятий.

В современной математике точкой называют элементы весьма различной природы, из которых состоят различные пространства (например, в n -мерном евклидовом пространстве точкой называют упорядоченную совокупность из n -чисел).

Во многих областях математики встречаются точки, имеющие специальные названия. Так, в геометрии изучаются особые точки кривых; в математическом анализе - особые точки решений дифференциальных уравнений, особые точки аналитических функций; в теории множеств - точки, характеризующие свойства рассматриваемого множества (предельная точка, граничная точка) и др.

Точка

1) единица длины, применяемая главным образом в полиграфии и равная 0,351460 мм.

2) Русская единица длинны, применявшаяся до введения метрической системы мер (1точка = 1/100 дюйма = 1/10 линии = 254 мкм).

Точка в ортогональной системе двух плоскостей проекций.

При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость является основание перпендикуляра, опущенного из данной точки на эту плоскость.

На рис. 7 показана точка А и ее ортогональные проекции А ₁ и А ₂, которые называют соответственно горизонтальной и фронтальной проекциями.

Проекции точки всегда расположены на прямой, перпендикулярной осиx ₂₁ и пересекающей эту ось в точке А _x.




а) модель б) эпюр
Рис.7. Точка в системе двух плоскостей проекций

Справедливо и обратное, т. е. если на плоскостях проекций даны точки А ₁ и А ₂ расположенные на прямой, пересекающей ось x ₂₁ в точке А _x под прямым углом, то они являются проекцией некоторой точки А.

На эпюре Монжа проекции А ₁ и А ₂ расположены на одном перпендикуляре к оси x ₂₁. При этом расстояние А ₁ А _x - от горизонтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П ₂, а расстояние А ₂ А _x - от фронтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П ₁.

Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.




а) модель	б) эпюр
Рис.8. Точки в различных четвертях пространства

На рис. 8 представлены точки A, B, C и D,расположенные в разных четвертях пространства и их эпюр (A - в первой, B - во второй, C - в третьей и D - в четвертой четвертях).

Точка в ортогональной системе трех плоскостей проекций.

В практике изображения различных геометрических объектов, чтобы сделать проекционный чертеж более ясным, возникает необходимость использовать третью – профильную плоскость проекций П ₃ расположенную перпендикулярно к П ₁ и П ₂.

Плоскости проекций П ₁, П ₂ и П ₃ являются основными плоскостями проекций.

а) модель б) эпюр Рис. 9. Точка в системе трех плоскостей проекций

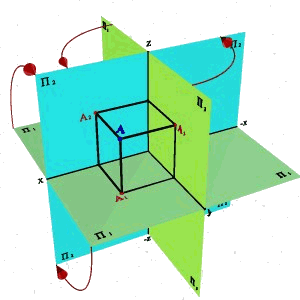Рис. 10. Получение эпюра Модель трех плоскостей проекций показана на рис.9. Третья плоскость, перпендикулярная и П ₁, и П ₂, обозначается буквой П ₃ и называется профильной. Проекции точек на эту плоскость обозначаются прописными буквами латинского алфавита или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П ₁ и П ₃ вращают, как показано на рис. 10, до совмещения с плоскостью П ₂. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координаты (от лат. со — совместно и ordinatus — упорядоченный, определенный) — числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. В 14 веке Н.Орем пользовался координатамина плоскости для построения графиков, называя долготой и широтой то, что теперь называют абсциссой и ординатой. Более систематически координаты стали применяться к вопросам геометрии на плоскости в 17 веке. Заслуга выяснения всего значения метода координат позволяющего систематически переводить задачи геометрии на язык математического анализа и обратно, истолковывать геометрически факты анализа, принадлежат Р. Декарту. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x, y и z (абсцисса, ордината и аппликата). Положение точки относительно плоскостей проекций. Положение точки в пространстве определяется тремя координатами x,y,z. Точка может занимать в пространствекак общее, так и частноеположение по отношению к плоскостям проекций.

Точка не принадлежащая ни одной из плоскостей проекций - точка общего положения.

Координаты точки общего положения не равны нулю (x≠0,y≠0,z≠0), и в зависимости от знака координаты точка может располагаться в одном из восьми октантов, как показано в таб.1 и на рис.11. Таблица 1. Знаки координат в октантах

точка	октант	координаты
x	y	z
A	I	+	+	+
B	II	+	-	+
D	III	+	-	-
C	IV	+	+	-
E	V	-	+	+
F	VI	-	-	+
N	VII	-	-	-
G	VIII	-	+	-

а) модель I-IV октантов





б) модель V-VIII октантов	в) эпюр
Рис.11. Точки общего положения

Точка принадлежит плоскости проекций (рис.12).

Точка А принадлежит горизонтальной плоскости проекций (x≠0,y≠0,z=0) - фронтальная проекция точки лежит на оси x, а профильная на оси y.
Точка B принадлежит фронтальной плоскости проекций (x≠0,y=0,z≠0) - горизонтальная проекция точки лежит на оси x, а профильная на оси z.
Точка С принадлежит профильной плоскости проекций (x=0,y≠0,z≠0) - горизонтальная проекция точки лежит на оси y, а фронтальная на оси z.




а) модель	б) эпюр
Рис. 12. Точки частного положения

Точка принадлежащая одновременно двум плоскостям проекций - точка на оси (рис.12).

Точка D лежит на оси x, принадлежит одновременно горизонтальной и фронтальной плоскостям проекций (x≠0,y=0,z=0).
Точка E лежит на оси y, принадлежит одновременно горизонтальной и профильной плоскостям проекций (x=0,y≠0,z=0).
Точка F лежит на оси z, принадлежит одновременно фронтальной и профильной плоскостям проекций (x=0,y=0,z≠0).

Точка принадлежит одновременно трем плоскостям проекций - 0 (x=0,y=0,z=0) - начало координат.

взаимное расположение точек.

Рассмотрим три основных варианта взаимного расположения точек, в зависимости от соотношения координат определяющих их положение в пространстве:

1. Рассмотрим точки А и В (рис.13), все три координаты которых отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций:

- Y_А>Y_В. Тогда точка А расположена дальше от плоскости П ₂ и ближе к наблюдателю, чем точка В;

- Z_А>Z_В. Тогда точка А расположена дальше от плоскости П ₁ и ближе к наблюдателю, чем точка В;

- X_А<X_В. Тогда точка В расположена дальше от плоскости П ₃ и ближе к наблюдателю, чем (при взгляде слева) точка А.

а) модель б) эпюр

Рис. 13. Взаимное расположение точек

2. На рис. 14 представлены точки А, В, С, D, у которых одна из координат совпадает, а две другие отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций следующим образом:

– Y_А=Y_В=Y_D, то точки А, В и D равноудалены от плоскости П ₂ и их горизонтальные и профильные проекции расположены, соответственно, на прямых А ₁ В ₁//x₁₂ и А ₃ В ₃// z. Геометрическим местом таких точек служит плоскость, параллельная П ₂;

– Z_А=Z_В=Z_С, то точки А,В и С равноудалены от плоскости П ₁ и их фронтальные и профильные проекции расположены, соответственно, на прямых А ₂ В ₂//x₁₂ и А ₃ С ₃// y. Геометрическим местом таких точек служит плоскость, параллельная П ₁;

– X_А=X_C=X_D, то точки А,C и D равноудалены от плоскости П ₃ и их горизонтальные и фронтальные проекции расположены, соответственно, на прямых А ₁ C ₁// y и А ₂ D ₂//z. Геометрическим местом таких точек служит плоскость, параллельная П ₃.

3. Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой. На рис. 14. даны три пары таких точек, у которых:

а) модель б) эпюр

Рис.14. Конкурирующие точки

· X_А= X_D; Y_А=Y_D; Z_D>Z_А;

· X_A= X_C; Z_A=Z_C; Y_C>Y_A;

· Y_A= Y_B; Z_A=Z_B; X_B>X_A.

Соответствующие проекции конкурирующих точек совпадают.

Различают:

· горизонтально конкурирующие точки А и D, расположенные на горизонтально проецирующей прямой АD;

· фронтально конкурирующие точки A и C расположенные на фронтально проецирующей прямой AC;

· профильно конкурирующие точки A и B, расположенные на профильно проецирующей прямой AB.

При проецировании на соответствующую плоскость проекций одна точка «закроет» другую точку, конкурирующую с ней, соответствующая проекция которой окажется невидимой.

Тест "Точка"

Точка С находится в первой четверти? Да Нет

Точка В находится во второй четверти? Да Нет

Точка А находится в первой четверти? Да Нет

Точка Д находится в третьей четверти? Да Нет

Точка Д лежит на горизонтальной плоскости проекций? Да Нет

Практикум по решению задач.

Тема: Проекции точки

Задача 1.

По наглядному изображению точек А,В,С,D и F построить эпюры;
Определить, где расположены точки, выписать их координаты.

Задача 2.

Построить недостающие проекции точек А,В,С,D и их наглядное изображение в системе трех плоскостей проекций.

Задача 3.

Построить пространственное изображение точки А (45,70,60) в системе трех плоскостей проекций, найти положение точек:
1. В симметричной точке А относительно оси x;
2. С симметричной точке В относительно плоскости П ₂;
3. Д расположенной на 20 мм дальше точки А от плоскости П ₃.
Построить эпюр полученных точек

Прямая линия.

Прямая линия

Способы графического задания прямой линии.

Положение прямой относительно плоскостей проекций.

Следы прямой.

Взаимное расположение точки и прямой.

Деление отрезка прямой линии в данном соотношении.

Определение длины отрезка прямой линии и углов наклона прямой к плоскостям проекций.

Взаимное расположение двух прямых.

Параллельные прямые линии.

Пересекающиеся прямые линии.

Скрещивающиеся прямые линии.

Проекции плоских углов.

Прямая линия - одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.

Прямая линия - алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением 1 - ой степени (линейное уравнение).

Общее уравнение прямой (полное):

Ах + Ву + С =0,

где А, В и С - любые постоянные, причем А и В одновременно не равны нулю. Если один из коэффициентов равен нулю, уравнение называется неполным.

Способы графического задания прямой линии.

Для определения положения прямой в пространстве существуют следующие методы:

1.Двумя точками (А и В).

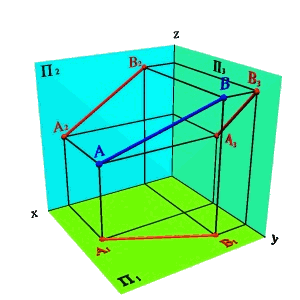
Рассмотрим две точки в пространстве А и В (рис. 15). Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка [BA] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка:

[A₁B₁]<[BA]; [A₂B₂]<[BA;] [A₃B₃]<[BA].

а) модель б) эпюр

Рис. 15. Определение положения прямой по двум точкам

Обозначим углы между прямой и плоскостями проекций через α - с плоскостью П₁, β - с плоскостью П₂, γ- с плоскостью П₃ и тогда получим:

|А₁В₁|=|BA|cos a

|A₂B₂|=|AB|cos b

|A₃B₃|=|AB|cos g.

Частный случай |A₁B₁|=|A₂B₂|=|A₃B₃| при таком соотношении прямая образует с плоскостями проекций равные между собой углы a=b=g=35⁰, при этом каждая из проекций расположена под углом 45⁰ к соответствующим осям проекций.

Двумя плоскостями (a; b).

Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).

Двумя проекциями.

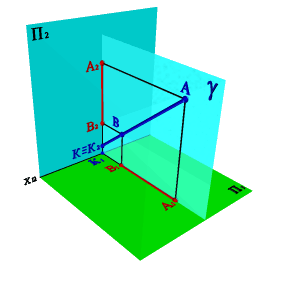
Пусть в плоскостях П₁ и П₂ даны проекции прямых заданных отрезками [А₁В₁] и [A₂B₂]. П роведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.16а), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А₁В₁] и [А₂В₂].

а)a непараллельная b б) a и b совпадают

Рис.16. Определение положения прямой в пространстве по двум проекциям отрезка

Плоскости a и b могут слиться в одну плоскость g, если, например, проекции [ А ₁ В ₁] и [ А ₂ В ₂] перпендикулярны оси x и пересекают ее в одной точке (рис.16б). Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П ₂.