Тесты(1 семестр)
1. Указать в каком из приведенных ниже примеров существует произведение матриц:
 2. Какая из однородных систем имеет только нулевое решение:
2. Какая из однородных систем имеет только нулевое решение:
 3.При каком значении параметра t данная система векторов из пространства
3.При каком значении параметра t данная система векторов из пространства  линейно зависима: а=(1,2,0), b=(5,t,2), c=(t,1,3).
линейно зависима: а=(1,2,0), b=(5,t,2), c=(t,1,3).
а) 7/32; б)5/7; в) 32/7; г) 1/7; д) 0.
4. Найти среди отображений  линейное:
линейное:
а)  , б)
, б)  , в)
, в) 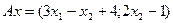 ,
,
г)  , д)
, д)  .
.
5. Найти, при каком значении параметра  векторы a и b ортогональны, если а=(1,-5,
векторы a и b ортогональны, если а=(1,-5,  ), b=(3,4
), b=(3,4  ,19).
,19).
а) -6, б) 6, в) 3, г) -12, д)12.
6. Среди прямых, заданных уравнениями, указать прямую, проходящую через точку А(1,2) параллельно вектору l=(-3;1):
а)  , б)
, б)  , в)
, в)  , г)
, г)  , д)
, д)  .
.
1 Установить, какая из записей верна:
 |
- Число 5 является образом элемента 2 при отображении

3.Множество {-3,3} является прообразом элемента 10 при отображении

4.Описать перечислением всех элементов заданные множества:

5.Описать перечислением всех элементов множества
 |
6.Доказать, что
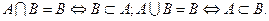
 |
7. Пусть А= (-1,2] и В =[1,4). Найти множества
и изобразить их на числовой оси.
Тесты (2 семестр)
8. Начиная, с какого наименьшего номера n члены последовательности 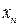 будут отличаться от своего предела на расстояние, меньшее чем
будут отличаться от своего предела на расстояние, меньшее чем  ?
?
8.1. 
8.2. 
8.3. 
8.4. 
Варианты ответов (для всех заданий): 1) 251; 2) 300; 3) 501; 4) 2000; 5) 2001; 6) нет верного ответа.
9. Найти 
9.1.  9.2.
9.2.  9.3.
9.3.  9.4.
9.4. 
Варианты ответов: 1) 0; 2) 1/5; 3) 1; 4) 3/7; 5)  ; 6) нет верного ответа.
; 6) нет верного ответа.
10. Найти 
10.1. 
10.3. 
10.2. 
10.4. 
Варианты ответов: 1) 0; 2) 0,5; 3) 2; 4) 3,2; 5) 4; 6) нет верного ответа.
11. Найти 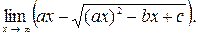
11.1. 
11.3. 
11.2. 
11.4. 
Варианты ответов: 1) 0; 2) 0,3; 3) 1; 4) 1,25; 5) 1,5; 6) нет верного ответа.
12. Найти область непрерывности, точки разрыва и их характер, если функция
 .
.
12.1. 
12.3. 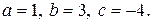
12.2. 
12.4. 
Варианты ответов:
1)  – точка устранимого разрыва,
– точка устранимого разрыва, 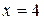 – точка разрыва второго рода; в остальных точках функция непрерывна;
– точка разрыва второго рода; в остальных точках функция непрерывна;
2)  – точка устранимого разрыва,
– точка устранимого разрыва,  – точка разрыва второго рода; в остальных точках функция непрерывна;
– точка разрыва второго рода; в остальных точках функция непрерывна;
3)  – точка устранимого разрыва,
– точка устранимого разрыва,  – точка разрыва второго рода; в остальных точках функция непрерывна;
– точка разрыва второго рода; в остальных точках функция непрерывна;
4)  – точка устранимого разрыва,
– точка устранимого разрыва,  – точка разрыва второго рода; в остальных точках функция непрерывна;
– точка разрыва второго рода; в остальных точках функция непрерывна;
5) одна точка разрыва второго рода, в остальных точках функция непрерывна;
6) нет верного ответа.
13. Найти  , если
, если  .
.
13.1. 
13.3. 
13.2. 
13.4. 
Варианты ответов:
1) 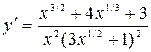 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6) нет верного ответа.
; 6) нет верного ответа.
14. Найти  , если
, если  .
.
14.1.  14.2.
14.2.  14.3.
14.3.  14.4.
14.4. 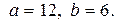
Варианты ответов:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6) нет верного ответа.
; 6) нет верного ответа.
15. Найти  , если
, если  .
.
15.1.  15.2.
15.2.  15.3.
15.3.  15.4.
15.4. 
Варианты ответов:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6) нет верного ответа.
16. Указать интервалы возрастания, выпуклости, точку максимума и точку перегиба графика функции 
16.1.  16.2.
16.2.  16.3.
16.3.  16.4.
16.4. 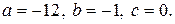
Варианты ответов:
1)  – интервал возрастания,
– интервал возрастания, 

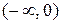 – интервал выпуклости, (0, 0) – точка перегиба;
– интервал выпуклости, (0, 0) – точка перегиба;
2)  – интервал возрастания,
– интервал возрастания, 

 – интервал выпуклости, (0, 1) – точка перегиба;
– интервал выпуклости, (0, 1) – точка перегиба;
3)  и
и  – интервалы возрастания,
– интервалы возрастания, 

 – интервал выпуклости, (0, 2) – точка перегиба;
– интервал выпуклости, (0, 2) – точка перегиба;
4)  и
и  – интервалы возрастания,
– интервалы возрастания, 

 – интервал выпуклости, (0, 1) – точка перегиба;
– интервал выпуклости, (0, 1) – точка перегиба;
5)  и
и  – интервалы возрастания,
– интервалы возрастания, 

 – интервал выпуклости, (0, 1) – точка перегиба;
– интервал выпуклости, (0, 1) – точка перегиба;
6) нет верного ответа.
Тесты (3 семестр)
18. Найти неопределенный интеграл  .
.
18.1. 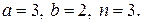
18.3. 
18.2. 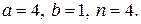
18.4. 
Варианты ответов:
1) 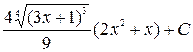 ;
;
3)  ;
;
5)  ;
;
2) 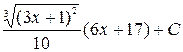 ;
;
4)  ;
;
6) нет верного ответа.
19. Найти неопределенный интеграл 
19.1. 
19.3. 
19.2. 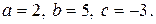
19.4. 
Варианты ответов:
1)  ;
;
3)  ;
;
5)  ;
;
2)  ;
;
4)  ;
;
6) нет верного ответа.
20. Найти неопределенный интеграл  .
.
20.1. 
20.3. 
20.2. 
20.4. 
Варианты ответов:
1)  ;
;
3) 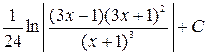 ;
;
5) 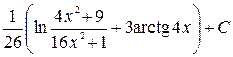 ;
;
2)  ;
;
4)  ;
;
6) нет верного ответа.
21. Найти определенный интеграл  .
.
21.1. 
21.2. 
21.3. 
21.4. 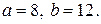
Варианты ответов: 1)  ; 2)
; 2) 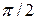 ; 3)
; 3)  ; 4)
; 4) 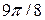 ; 5)
; 5)  ; 6) нет верного ответа.
; 6) нет верного ответа.
22. Найти несобственный интеграл 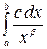 .
.
22.1.  22.3.
22.3. 
22.2. 
22.4. 
23. Варианты ответов: 1) первого рода расходится; 2) второго рода, расходится; 3) второго рода, 2; 4) первого рода, 2; 5) второго рода, 2/3; 6) нет верного ответа.
Показать, что данная функция удовлетворяет заданному равенству:  :
:  .
.
Варианты ответов: 1) да; 2) нет
24. Решить графическим методом задачу линейной оптимизации
 Варианты ответов: 1) х=(1,2), fmax=1 2)x=(2,0), fmax=2,
Варианты ответов: 1) х=(1,2), fmax=1 2)x=(2,0), fmax=2,
3) x=(7,1), fmax=1 4) x=(8,0), fmax=8
25. Дана задача линейного программирования:  при ограничениях
при ограничениях 
1) Выбрать допустимое решение задачи:
а) (0,2,1), б) (1,1,0), в) (1,-2,0);
2) Выбрать оптимальное решение задачи:
а) zmax= z(4,3,0) =12, б) zmax= z(2,-1,-1) =18, в) zmax= z(5,1,1) =19;
3) Определить направление (вектор) возрастания целевой функции:
а) (5,-3,1); б) (5,-4, 1), в) (5,-3,-4).
26. Дана задача линейного программирования:


 .
.
Определите, какие из данных целочисленных планов:  будут допустимыми. Среди допустимых планов укажите оптимальный план.
будут допустимыми. Среди допустимых планов укажите оптимальный план.
27. 1). Определить в каком из следующих случаев транспортной задачи следует ввести фиктивный пункт отправления, чтобы сбалансировать модель:
а) Предложение: а1=10, а2=5, а3=4, а4=6. Спрос: b1=10, b2=5, b3=7, b4=9;
б) Предложение: а1=30, а2=44. Спрос: b1=25, b2=30, b3=10;
в) Предложение: а1=60, а2=80, а3=100. Спрос: b1=40, b2=60, b3=80, b4=60.
2). Сколько базисных переменных должен содержать план выбранной транспортной задачи, чтобы он был опорным: а) 5, б) 8, в) 6.
28. Дана сетевая модель, определить каким множеством ребер она задана.
:
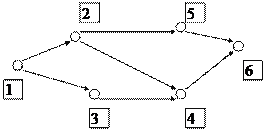 а) {(1,2), (1,3),(2,3),(2,5),(4,6),(5,6),(3,4)},
а) {(1,2), (1,3),(2,3),(2,5),(4,6),(5,6),(3,4)},
б) {(1,2), (1,3),(2,4),(2,5),(5,6),(3,4),(4,6)},
в) {(1,2), (1,3),(2,5), (3,4),(4,5), (5,6),((4,6)}.
4.2. Вопросы к экзамену(1семестр)
1. Понятие матрицы. Виды матриц.
2. Операции над матрицами: сложение, умножение на число, произведение матриц, операция транспонирования. Свойства операций.
3. Определители квадратных матриц. Определители 2-го и 3-го порядков.
4. Понятие об определителе n-го порядка.
5. Основные свойства определителей.
6. Миноры и алгебраические дополнения.
7. Теорема разложения.
8. Теорема аннулирования.
9. Обратная матрица. Теорема о существовании обратной матрицы.
10. Ранг матрицы.
11. Системы линейных алгебраических уравнений. Основные определения: решение, совместные и несовместные, определенные и неопределенные, равносильные системы. Элементарные преобразования.
12. Метод Крамера решения квадратных систем.
13. Метод Жордана-Гаусса исследования и решения систем линейных уравнений. Базисные и свободные неизвестные. Общее, частное и базисное решения.
14. Модифицированные жордановы исключения, применение к решению систем линейных уравнений.
15. Нахождение базисных решений с помощью МЖИ.
16. Однородные системы линейных уравнений.
17. Матричная запись системы линейных уравнений. Матричный метод решения.
18. Определение векторного пространства. Примеры векторных пространств. Пространство  .
.
19. Линейная зависимость и независимость системы векторов. Свойства.
20. Размерность и базис линейного пространства. Основные теоремы о размерности и базисе.
21. Разложение вектора по данному базису. Единственность разложения. Координаты вектора в данном базисе.
22. Формула перехода от одного базиса к другому.
23. Евклидово пространство. Скалярное произведение векторов и его свойства.
24. Норма вектора. Неравенство Коши-Буняковского. Угол между векторами.
25. Ортогональные и ортонормированные системы векторов. Ортонормированный базис. Теорема о существовании ортонормированного базиса в евклидовом пространстве.
26. Линейные операторы. Матрица линейного оператора в данном базисе.
27. Матрица линейного оператора в различных базисах. Формула перехода.
28. Собственные векторы и собственные значения линейного оператора.
29. Матрица линейного оператора в базисе из собственных векторов.
30. Квадратичные формы. Матрица квадратичной формы. Приведение квадратичной формы к каноническому виду.
31. Аналитическая геометрия на плоскости. Общее уравнение прямой.
32. Частные виды уравнений прямой: уравнение прямой с угловым коэффициентом, уравнение прямой по двум точкам, уравнение пучка прямых.
33. Угол между прямыми. Условия параллельности и перпендикулярности.
34. Кривые 2-го порядка.
35. Аналитическая геометрия в пространстве. Общее уравнение плоскости. Вектор нормали. Угол между плоскостями. Условия параллельности и перпендикулярности.
36. Уравнения прямой в пространстве. Направляющий вектор прямой. Угол между прямыми.
37. Гиперплоскость в n-мерном пространстве.
38. Выпуклое множество. Угловая (крайняя) точка выпуклого множества.
39. Система линейных неравенств.
Вопросы к зачету (2 семестр)
- Элементы теории множеств.
1.1.Понятие множества. Способы задания множеств.
1.2.Операции над множествами.
1.3. Декартово произведение множеств.
1.4. Отображения, функции. Образ и прообраз элемента, множества.
1. Числовые множества.
2.1. Числовые множества. Расширенная числовая прямая.
2.2 Промежутки действительных чисел. Окрестности точек. Окрестности символов 
2.3 Абсолютная величина действительного числа и ее свойства.
2.4 Ограниченные и неограниченные множества.
2.5 Верхняя и нижняя грани числовых множеств. Теорема существования.
2. Числовые функции.
3.1.Понятие функции. Область существования, множество значений. Способы задания. График функции.
3.2. Монотонные функции. Ограниченные функции. Сложная функция. Обратная функция.
3.3.Элементарные функции и их классификация.
3. Числовые последовательности.
4.1.Понятие числовой последовательности. Ограниченные и неограниченные числовые последовательности.
4.2.Предел числовой последовательности. Геометрическая интерпретация предела последовательности.
4.3. Сходящиеся последовательности. Свойства сходящихся последовательностей.
4.4. Монотонные последовательности. Теорема о сходимости монотонной, ограниченной последовательности. Число e.
5.Предел функций.
5.1. Предельные точки множества. Конечные и бесконечные пределы функций в конечных и бесконечных предельных точках. Геометрический смысл понятий предела.
5.2.Свойства функций, имеющих конечный предел. Односторонние пределы.
5.3.Бесконечно малые и бесконечно большие функции.
5.4. Основные теоремы о бесконечно малых функциях: об алгебраической сумме бесконечно малых функций, о произведении бесконечно малой на ограниченную функцию.
5.5. Основные теоремы о бесконечно больших функциях.
5.6. Понятие о неопределенностях. Основные виды неопределенностей.
5.7. Критерий существования конечного предела функции.
5.7. Теоремы о пределе суммы, произведения, частного.
5.8. Предел сложной функции.
5.9. Теорема о пределе промежуточной функции, о предельном переходе в неравенствах.
6 Непрерывность функции.
6.1. Два определения непрерывности функции в точке. Их эквивалентность. Непрерывность функции на множестве.
6.2. Понятие об односторонней непрерывности функции в точке.
6.2. Теоремы о непрерывности суммы, произведения и частного непрерывных функций.
6.3. Непрерывность сложной функции.
6.4. Непрерывность элементарных функций.
6.5. Условия непрерывности функций в точке. Точки разрыва и их классификация.
6.6. Основные теоремы о функциях непрерывных на отрезке: теорема Вейерштрасса, теорема Больцано, теорема о промежуточном значении непрерывной на отрезке функции.
7 Производная функции.
7.1. Определение производной функции в точке и ее геометрический смысл. Уравнение касательной.
7.2. Необходимое условие существования производной.
7.3. Основные правила дифференцирования.
7.4. Производная сложной функции.
7.5 Производная обратной функции.
7.6. Дифференцируемые функции. Условия дифференцируемости.
7.7. Дифференциал функции и его геометрический смысл.
7.8. Основные свойства дифференциала. Инвариантность формы дифференциала.
8. Теоремы о дифференцируемых функциях.
8.1 Теорема Ферма ее геометрический смысл.
8.2. Теорема Ролля и ее геометрический смысл.
8.3 Теорема Лагранжа и ее геометрический смысл.
8.4. Правило Лопиталя.
8.5. Формула Тейлора. Различные формы остаточного члена.
8.6. Формула Маклорена.
9.Исследование функций.
9.1 Необходимое и достаточное условия монотонности функции.
9.2 Экстремум функции. Необходимое условие экстремума.
9.3 Первое достаточное условие экстремума.
9.4 Второе достаточное условие экстремума.
9.5 Понятие выпуклости и вогнутости графика функции.
9.6 Признаки выпуклости и вогнутости.
9.7 Точки перегиба. Достаточное условие точки перегиба.
9.8. Наибольшее и наименьшее значения функции на отрезке.
Вопросы к экзамену (3 семестр)
1. Неопределенный интеграл.
1.1. Первообразная функция. Теорема о первообразных.
1.2. Неопределенный интеграл и его свойства.
1.3. Таблица неопределенных интегралов.
1.4. Метод подстановки в неопределенном интеграле.
1.5. Интегрирование по частям в неопределенном интеграле.
1.6. Понятие об интегралах, не выражающихся в элементарных функциях.
2. Определенный интеграл.
2.1. Понятие интегральной суммы. Предел интегральной суммы.
2.2. Определение определенного интеграла. Геометрический смысл определенного интеграла.
2.3. Теорема существования определенного интеграла.
2.4. Свойства определенного интеграла, выраженные равенствами.
2.5. Свойства определенного интеграла, выраженные неравенствами.
2.6. Теорема о среднем.
2.7. Определенный интеграл с переменным верхним пределом. Теорема о дифференцируемости.
2.8. Формула Ньютона-Лейбница.
2.9. Замена переменной в определенном интеграле.
2.10. Интегрирование по частям в определенном интеграле.
2.11. Геометрические приложения определенного интеграла.
2.12. Несобственные интегралы 1-го рода.
2.13. Несобственные интегралы 2-го рода.
3. Функции многих переменных.
3.1. Понятие n-мерного координатного и n-мерного евклидова пространства. Открытый шар. Окрестность точки.
3.2. Понятие функции многих переменных. Область определения, множество значений. Примеры.
3.3. Поверхности и линии уровня.
3.4. Предельные точки множества. Предел функции многих переменных.
3.5. Бесконечно малые и бесконечно большие функции. Ограниченные функции многих переменных.
3.6. Полное приращение функции. Непрерывность функции многих переменных.
3.7. Понятие замкнутого ограниченного множества. Свойства функций непрерывных на замкнутом ограниченном множестве.
3.8. Частные приращения и частные производные функции многих переменных.
3.9. Дифференцируемость функции многих переменных.
3.10. Полный дифференциал функции многих переменных.
3.11. Понятие сложной функции многих переменных. Непрерывность сложной функции.
3.12. Теорема о производной сложной функции.
3.13. Производная по направлению.
3.14. Градиент функции многих переменных. Свойства градиента.
3.15. Понятие неявной функции. Производная неявной функции.
3.16. Частные производные высших порядков. Теорема о равенстве смешанных производных второго порядка.
4. Экстремум функции многих переменных.
4.1. Понятие локального экстремума функции многих переменных. Критическая точка градиента. Необходимое условие локального экстремума.
4.2. Понятие квадратичной формы. Критерий Сильвестра. Гессиан.
4.3. Достаточные условия локального экстремума. Случай двух переменных.
4.4. Понятие условного экстремума. Уравнение связи. Функция Лагранжа.
4.5. Необходимое условие условного экстремума.
4.6. Достаточное условие условного экстремума.
4.7. Наибольшее и наименьшее значения функции в замкнутом, ограниченном множестве.
4.8. Функция полезности и потребительский спрос. Кривые безразличия. Бюджетное ограничение. Задача максимизации функции полезности при данном бюджете потребителя.
Вопросы к зачету (4 семестр)
1.Математическая постановка задач линейного программирования. Примеры типовых задач: задача оптимального планирования; задача о диете.
2. Различные формы задач ЛП: общая, стандартная и каноническая. Переход от одной формы задачи ЛП к другой. Запись задач ЛП в матричной форме.
3. Основные определения: допустимое, оптимальное, опорное решения, область допустимых решений. Неразрешимость задач линейного программирования.
4. Свойство решений задач ЛП. Фундаментальная теорема.
5. Идея симплекс-метода. Симплекс-таблицы. Симплексные отношения. Переход от одного опорного плана к другому.
6. Критерий оптимальности опорного плана задачи ЛП.
7. Условия неограниченности целевой функции. Условия улучшения опорного плана (теорема).
8. Алгоритм симплексного метода. Понятие зацикливания в случае вырожденности опорного плана.
9. Решение задачи ЛП, когда среди свободных членов системы ограничений есть отрицательные.
10. Решение общей задачи ЛП. Особенности приведения системы ограничений к единичному базису. Алгоритм решения общей задачи ЛП.
11.Понятие о двойственных задачах линейного программирования. Прямая и двойственная задачи. Экономический смысл двойственных переменных.
12. Симметричные двойственные задачи. Правила построения двойственной задачи. Связь между решениями прямой и двойственной задач.
13.Основное неравенство двойственности. Экономическая интерпретация.
14. Первая теорема двойственности. Экономическая интерпретация. Двойственные симплекс-таблицы.
15. Вторая теорема двойственности. Экономическая и геометрическая интерпретация. 16. Понятие о несимметричных двойственных задачах.
17. Транспортная задача (ТЗ). Содержательная постановка ТЗ. Математическая модель ТЗ.
18. Критерий разрешимости ТЗ. Ранг матрицы ТЗ. Вырожденный и невырожденный опорный план.
19. Определение исходного опорного плана. Метод «северо-западного угла». Метод «наименьшей стоимости».
20. Понятие цикла. Переход от одного опорного плана к другому сдвигом по циклу пересчета.
21.Достаточные условия оптимальности опорного плана ТЗ. Построение системы потенциалов.
22. Алгоритм решения ТЗ методом потенциалов.
23. Открытая модель ТЗ.
24. Элементы теории игр. Предмет и основные понятия теории игр: стратегия, оптимальная стратегия, платежная матрица. Классификация игры.
25. Игры двух лиц с нулевой суммой. Смешанная и чистая стратегии, функция выигрыша, седловой элемент платежной матрицы, цена игры. Понятие об игре, разрешимой в чистых стратегиях. Максиминные и минимаксные стратегии игроков. Теорема о разрешимости игры в чистых стратегиях.
26. Смешанные стратегии. Функция выигрыша (платежная функция). Оптимальные стратегии. Теорема Неймана.
27. Решение матричных игр 2×2, m×2, 2×n. Свойства оптимальных решений. Геометрическая интерпретация.
28. Упрощение платежной матрицы. Принцип доминирования.
29.Сведение матричной игры к паре двойственных задач линейного программирования.
- Классификация математических моделей и прикладных задач дискретного программирования.
- Понятие о целочисленном программировании. Постановка задачи. Экономическая и геометрическая интерпретация.
- Метод Гомори решения задач целочисленного программирования.
33. Комбинаторные методы дискретного программирования. Метод ветвей и границ.
34. Постановка задачи нелинейного программирования. Экономическая и геометрическая интерпретация. Решение методом множителей Лагранжа.
35. Задачи нелинейного программирования при ограничениях-неравенствах. Теорема Куна-Таккера. Седловая точка.
36. Квадратичное программирование.
37. Общая характеристика задач динамического программирования и их геометрическая и экономическая интерпретация. Метод динамического программирования. Принцип оптимальности Беллмана. Функциональное уравнение Беллмана.
38. Задача об оптимальном распределении инвестиций между предприятиями.
39. Задача о замене оборудования.
40. Программирование на сетях Понятие графа. Способы задания. Сети. Потоки в сетях.
41. Постановка задачи о нахождении максимального потока в сети. Алгоритм Форда-Фалкерсона нахождения максимального потока.
42. Задача нахождения кратчайшего пути в сети и потока наименьшей стоимости.
4.3. Типы задач
1. Вычислить определители: 
2. Решить системы линейных уравнений различными методами:
а)  б)
б)  Найти все базисные решения. в)
Найти все базисные решения. в)  г)
г) 
3. Выяснить являются векторы а1, а2, а3 линейно зависимыми или линейно независимыми, в случае линейной зависимости привести пример нетривиальной линейной комбинации, равной нулевому вектору: 
4. Показать, что векторы{a1, a2, a3} образуют базис. Разложить вектор b по базису векторов {a1, a2, a3},где  ,b=(2,0,1).
,b=(2,0,1).
5. Найти параметрическое уравнение прямой L, проходящей через точку х0=(2,1,-1) перпендикулярно плоскости 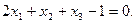 , и угол между прямой L и плоскостью
, и угол между прямой L и плоскостью 
6. Найти уравнение плоскости (a), проходящей через точки х0=(1,3,-4) и х1=(0,5,1) параллельно прямой L:  , и угол между плоскостью (a) и плоскостью
, и угол между плоскостью (a) и плоскостью 
7. Найти параметрическое уравнение прямой L:  и угол между прямой L и плоскостью
и угол между прямой L и плоскостью 
8. Найти матрицу линейного оператора А(х)=  в каноническом базисе.
в каноническом базисе.
9. Дан оператор  , А(х)=
, А(х)=  и базис f ={ f1, f2 }=
и базис f ={ f1, f2 }=  в
в  . Найти матрицу оператора в этом базисе: по определению и по теореме об изменении матрицы при переходе к другому базису.
. Найти матрицу оператора в этом базисе: по определению и по теореме об изменении матрицы при переходе к другому базису.
10. Построить квадратичную форму, заданную матрицей А в  , А=
, А=  . Привести ее к каноническому виду и найти ортонормированный базис, в котором она имеет этот.
. Привести ее к каноническому виду и найти ортонормированный базис, в котором она имеет этот.
1.Найти оптимальное решение методом Гомори.



2. Три типа самолетов следует распределить между четырьмя авиалиниями. В таблице приведены данные месячного объема перевозок каждым самолетом на каждой линии и соответствующих эксплуатационных расходов.
| Тип самолета | Число самолетов | Месячный объем перевозок 1 самолетом по авиалиниям | Эксплуатационные расходы на 1 самолет по авиалиниям | ||||||
Распределить самолеты по линиям так, чтобы при минимальных суммарных эксплуатационных расходах перевезти по каждой из четырех авиалиний не менее 300, 200, 1000 и 500 ед. груза соответственно.
3. Найти максимальный поток в сети методом расстановки пометок.


 |  | ||||
 | |||||

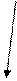


Даны пропускные способности дуг: С(0;1)=1, С(0;2)=4, С(1;2)=1, С(2;1)=2, С(1;3)=3, С(2;3)=2, С(2;4)=2, С(3;5)=4, С(4;5)=1.
1. Решить транспортную задачу.

| ||||
1. Решить транспортную задач
| ||||||
2. Найти цену игры с платежной матрицей.

7. Найти решение игры с матрицей  .
.
8.Решить игру, заданную платежной матрицей, сведя ее к паре двойственных задач линейного программирования.
П= 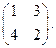
4.4. Заданиедля студентов заочной формы обучения.
Домашнее задание представляет собой письменную работу, призванную продемонстрировать степень усвоения знаний, приобретенных студентом в ходе самостоятельной подготовки. Задание состоит из 10 вариантов задач по темам: системы линейных уравнений, векторные пространства,линейные операторы, квадратичные формы, элементы аналитической геометрии, линейные задачи оптимизации. Задание должно быть оформлено в отдельной тетради. На титульном листе должно быть необходимо название предмета, специальность, ФИО, факультет, группа, шифр.
Задачи выполняются в следующей последовательности.
1. Описать постановку задачи.
2. Описать математический аппарат, используемый для решения задачи.
3. Решение задач.
Сдача контрольной работы производится в форме собеседования, в ходе которого студент сначала кратко излагает основные выводы и результаты работы и отвечает на замечания, отмеченные в рецензии. По результатам защиты выставляется окончательная оценка, которая учитывает и ответы студента на вопросы, если они были заданы преподавателем.
4.4. Билеты к экзамену (1 семестр)
Билет№1
1.Линейные операции над матрицами и их свойства.
2.Матрица линейного оператора.
3.Решить систему по формулам Крамера

4. Найти точку пересечения прямой  с плоскостью
с плоскостью 
5. Записать матрицу квадратичной формы 
Билет№2
1.Произведение матриц. Основные свойства произведения матриц.
2.Уравнение прямой с угловым коэффициентом. Геометрический смысл параметров.
3. Показать, что векторы  образуют базис в
образуют базис в  . Разложить вектор
. Разложить вектор  по этому базису.
по этому базису.
4. Найти собственные векторы и собственные значения линейного оператора, заданного матрицей 

5. Записать матрицу квадратичной формы.

Билет№3
1.Определители 2-го и 3-го порядков и их свойства.
2.Математическая модель задачи линейного программирования. Основные определения: допустимый план, опорный план, оптимальный план.
3.Найти все базисные решения системы методом ИЖИ

4. Найти параметрические уравнения прямой, проходящей через точки

5. Линейный оператор 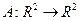 задан матрицей
задан матрицей 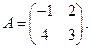 Найти образ
Найти образ

Билет№4
1.Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца.
2. Евклидово пространство. Скалярное произведение векторов. Свойства скалярного произведения.
3. Исследовать на линейную зависимость систему векторов 
4. Записать уравнение прямой, проходящей через точку  перпендикулярно прямой x-2y+11=0.
перпендикулярно прямой x-2y+11=0.
5. Записать задачу двойственную к задаче


Билет№5
1.Обратная матрица. Теорема о существовании и единственности обратной матрицы.
2.Ортогональные и ортонормированные системы векторов.
3.Решить систему методом Жордана-Гаусса

4. Даны вершины треугольника А (-4;0), В (-2;6), С (2;2). Найти уравнение высоты AF.
5.Привести данную квадратичную форму к каноническому виду

Билет№6
1. Определение векторного пространства. Пространство 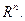
2. Канонические уравнения прямой в пространстве.
3. Найти матрицу 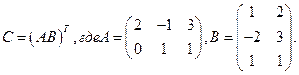
4. Исследовать на линейную зависимость систему векторов 
5. Решить графическим методом ЗЛП 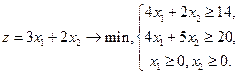
Билет№7
1. Линейная комбинация системы векторов. Линейно зависимые и независимые системы векторов. Основные свойства.
2. Первая теорема двойственности. Экономический смысл двойственных переменных.
3. Решить матричным способом систему уравнений 
4. Записать уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости 
5. Найти собственные векторы и собственные значения линейного оператора, заданного матрицей 
Билет№8
1. Размерность и базис векторного пространства. Критерий базисности системы векторов в пространстве 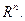
2. Уравнение плоскости в пространстве. Вектор нормали.
3. Найти все базисные решения системы методом МЖИ 
4. Даны вершины треугольника А (-4;0), В (-2;6), С (2;2). Найти уравнение медианы АЕ.
5. Дан вектор  в базисе
в базисе  Найти координаты вектора x в базисе
Найти координаты вектора x в базисе  с помощью матрицы перехода.
с помощью матрицы перехода.
Билет№9
1. Разложение вектора по векторам базиса. Единственность разложения. Координаты вектора.
2. Угол между прямыми на плоскости. Условия параллельности и перпендикулярности.
3.  Найти обратную матрицу
Найти обратную матрицу  Сделать проверку.
Сделать проверку.
4. Найти собственные векторы и собственные значения линейного оператора, заданного матрицей 
5. Дана задача ЛП. 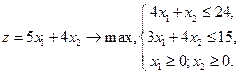 Составить двойственную задачу.
Составить двойственную задачу.
Билет№10
1.Норма вектора. Неравенство Коши –Буняковского. Угол между
векторами.
2. Свойства множества допустимых планов задачи ЛП. Фундаментальная теорема.
3. Решить систему по формулам Крамера 
4.Исследовать на линейную зависимость систему векторов 
5.Найти точку пересечения прямой  и плоскости
и плоскости 
Билет№11
1. Линейные операторы. Матрица линейного оператора.
2. Угол между плоскостями в пространстве. Условие параллельности и перпендикулярности.
3. Решить матричным способом систему уравнений 
4.  Привести данную квадратичную форму к каноническому виду.
Привести данную квадратичную форму к каноническому виду.
5. Найти угловые точки множества решений системы неравенств 
Билет№12
1. Собственные векторы и собственные значения линейного оператора. Независимость характеристического многочлена линейного оператора от выбора базиса.
2. Угол между прямой и плоскостью в пространстве. Условие параллельности и перпендикулярности.
3. Показать, что векторы  образуют базис в
образуют базис в  . Найти координаты вектора
. Найти координаты вектора  в этом базисе.
в этом базисе.
4. Найти 
5. Решить графическим методом задачу ЛП 
Билет№13
1.Определение матрицы. Частные виды матриц.
2.Матрица линейного оператора в базисе из собственных векторов.
3. Решить систему методом Жордана-Гаусса 
4.Составить уравнение прямой, проходящей через точку М (-1;2) параллельно прямой 
5.Привести квадратичную форму  к каноническому виду.
к каноническому виду.
Билет№14
1. Системы линейных уравнений. Основные понятия и определения.
2. Зависимость между матрицами линейного оператора в разных базисах.
3. 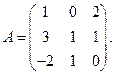 Найти обратную матрицу
Найти обратную матрицу  . Сделать проверку.
. Сделать проверку.
4. Записать параметрические уравнения прямой, проходящей через точки 
5. Решить симплексным методом задачу ЛП 
Билет№15
1. Матричная форма записи системы линейных уравнений. Матричный способ решения.
2. Динамическое программирование. Принцип оптимальности Беллмана.
3. Исследовать на линейную зависимость векторы 
4. Записать уравнения прямой, проходящей через точку  параллельно вектору
параллельно вектору 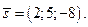
5. Записать матрицу квадратичной формы 
Билеты к экзамену (3семестр)
Билет№1.
1. Определение монотонности функции. Необходимое и достаточное условия монотонности.
2.Понятие интегральной суммы. Предел интегральной суммы.
-

-
 .
. - Найти точки перегиба и интервалы выпуклости и вогнутости функции

Билет№2.
1.Понятие выпуклости и вогнутости графика функции. Признаки выпуклости (вогнутости).
2. Определение определенного интеграла. Геометрический смысл определенного интеграла.
2. 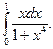
3. Найти производную по направлению 
4. 
Билет№3.
1.Точки перегиба. Необходимое и достаточное условия точки перегиба.
2. Неопределенный интеграл. Теорема существования.
3. 
4. z=sin(2x+3y). Показать, что данная функция удовлетворяет условию
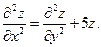
5. Найти экстремумы функции 
Билет№4.
1.Свойства определенного интеграла, выраженные равенствами.
2. Предел функции многих переменных.
3. 
4.  Найти
Найти  в точке М (1;2). Построить линию уровня, проходящую через точку М и градиент.
в точке М (1;2). Построить линию уровня, проходящую через точку М и градиент.
5. Найти асимптоты графика функции 
Билет№5.
1.Свойства неопределенного интеграла.
2. Точечные множества в n-мерном пространстве. Окрестность точки. Предельная точка множества.
3. 
4. Найти частные производные







