Цикла ЕН по специальности 080100

Рассмотрено и УТВЕРЖДАЮ

Рекомендовано

на заседании кафедры Декан факультета

Фундаментальной и прикладной

математики проф. Денисов М.Ю.

Протокол №_____1______ _______________

«_5__» ___сентября__2009г. _______________

Зав. кафедрой проф. В.И. Седенко

__________________ «___» __________200_г.

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

учебной дисциплины «Математика»

цикла ЕН по специальности 080100

Экономика (Бакалавариат)

Составитель: ст. преподаватель Киселева Н.Н.

Ростов-на-Дону

2009г.

СОДЕРЖАНИЕ

Рабочая программа дисциплины 3

1. Цели и задачи дисциплины. 4

1.1. Цель. Задачи дисциплины, ее место в подготовке специалиста (с учетом квалификационных требований ГОС)

1.2. Требования к уровню усвоения дисциплины 4

1.3. Связь с другими дисциплинами Учебного плана

1.4. Содержание дисциплины, способы и методы учебной деятельности преподавателя

1.5. Аудиторные занятия (лекции, практические) 5

1.6. Индивидуальная работа преподавателя со студентами 18

1.7. Самостоятельная работа студента 20

1.8. Инновационные способы и методы, используемые в

образовательном процессе 24

3. Средства обучения 24

3.1. Информационно-методические

3.2. Материально-технические

4. Контроль знаний студентов 26

4.1. Тесты

4.2. Вопросы к зачету и экзамену 33

4.3. Типы задач 38

4.4. Экзаменационные билеты 41

5.Дополнение и изменения в рабочей программе на учебный год 52

Выписка из ГОС ВПО по специальности «Математические методы в

экономике» 52

Краткое изложение программного материала 53

Методические указания по самостоятельной работе студентов 207

Деловая игра 208

Глоссарий 209

Сведения о ППС 215

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ «РИНХ»

РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА УТВЕРЖДАЮ:

ДИСЦИПЛИНЫ

Проректор Н.П.Маслова

___________________________

ЕН.Ф.01. Математика

(индекс) (наименование)

СПЕЦИАЛЬНОСТЬ(И)

080100 Экономика

(код) (наименование)

ФАКУЛЬТЕТ		Информатизации и управления
КАФЕДРА		Фундаментальной и прикладной математики

(код) (наименование)

ОБЩИЙ ОБЪЕМ^* работы студента в час.	ГОС	уч. план	Очная форма	Заочная форма
		4лет
Всего аудиторных занятий, час, в том числе:
- лекций, по семестрам	36/36/36/36
1/2/3/4
- лабораторные работы (или занятия по подгруппам), по семестрам

- практические занятия, по семестрам	54/54/54/54
1/2/3/4
Индивидуальная работа, час
Всего самостоятельной работы, час, в том числе:
- контрольные работы по семестрам
- курсовые работы по семестрам
- курсовые проекты по семестрам
- др. виды работы по семестрам
Зачеты, по семестрам, час	2, 4 семестр
Экзамены, по семестрам, час	1, 3 семестр

^* Объем часов по всем видам работ переносится из учебного плана.

ГОС ВПО по специальности 080100«Экономика» утвержден 14.04.2000г. Учебный план по специальности 080100 «Экономика» одобрен ученым Советом вуза 30.06.2009г. протокол № 6.

Нормативные документы и реквизиты (ГОС, Учебный план, примерная программа и др.,)

АВТОР cт.преподаватель		Киселева Н.Н.
(ученая степень, звание, должность)	(подпись)	(Ф.И.О.)	(дата)

ОБСУЖДАЛАСЬ И СОГЛАСОВАНА

Кафедрой ФиПМ		Седенко В.И..
(наименование)	(подпись)	(Ф.И.О.)	(дата)

Учебно-методическим советом специальности

Учебно-методическим управлением

1. Цели и задачи дисциплины

1.1. Цель. Задачи дисциплины, ее место в подготовке специалиста (с учетом квалификационных требований ГОС)

-приобрести твердые навыки решения математических задач с доведением до практически приемлемого результата и развить на этой базе логическое и алгоритмическое мышление; ---выработать первичные навыки математического исследования прикладных вопросов и развить необходимую интуицию в вопросах приложения математики; -выработать умения самостоятельно разбираться в математическом аппарате, содержащемся в литературе, связанной со специальностью студента; -уметь при решении задач выбирать и использовать необходимые вычислительные методы и средства (ПК, таблицы, справочники). Дисциплина является естественнонаучной и входит в федеральный компонент ГОС ВПО

1.2. Требования к уровню усвоения дисциплины

Студент должен знать: основные понятия и методы линейной алгебры, аналитической геометрии, математического анализа, дифференциальных уравнений; математические методы и модели исследования экономических систем.

Студент должен уметь решать системы линейных уравнений; выполнять операции над матрицами и векторами; составлять уравнения прямой, плоскости, кривых второго порядка; находить пределы последовательностей и функций, производные и дифференциалы первого и высших порядков; применять производные к решению задач оптимизации; вычислять первообразные функции (в простейших функциях), определенные интегралы; решать обыкновенные дифференциальные уравнения; употреблять математическую символику для выражения количественных и качественных отношений объектов.

Студент должен иметь представление о математике как особом способе познания мира, общности ее понятий и представлений; о принципах математических рассуждений и доказательств, об алгебраических структурах на множествах, о математическом моделировании.

1.3. Связь с другими дисциплинами Учебного плана

Перечень действующих дисциплин с указанием разделов (тем)	Перечень последующих дисциплин, видов работ
Экономическая теория	Теория вероятностей и математическая статистика Математическое моделирование экономических систем Микроэкономика Макроэкономика Математические методы исследования в экономике Дипломное проектирование

2. Содержание дисциплины, способы и методы учебной деятельности преподавателя

Методы обучения – система последовательных, взаимосвязанных действий, обеспечивающих усвоение содержания образования, развитие способностей студентов, овладение ими средствами самообразования и самообучения; обеспечивают цель обучения, способ усвоения и характер взаимодействия преподавателя и студента; направлены на приобретение знаний, формирование умений, навыков, их закрепление и контроль.

Монологический (изложение теоретического материала в форме монолога)	М
Показательный (изложение материала с приемами показа)	П
Диалогический (изложение материала в форме беседы с вопросами и ответами)	Д
Эвристический (частично поисковый) (под руководством преподавателя студенты рассуждают, решают возникающие вопросы, анализируют, обобщают, делают выводы и решают поставленную задачу)	Э
Проблемное изложение (преподаватель ставит проблему и раскрывает доказательно пути ее решения)	ПБ
Исследовательский (студенты самостоятельно добывают знания в процессе разрешения проблемы, сравнивая различные варианты ее решения)	И
Программированный (организация аудиторной и самостоятельной работы студентов осуществляется в индивидуальном темпе и под контролем специальных технических средств)	ПГ
Другой метод, используемый преподавателем (формируется самостоятельно), при этом в п.п. 2.1.-2.4. дается его наименование, необходимые пояснения

Приведенные в таблице сокращения обозначения педагогических методов используются составителем Рабочей программы для заполнения п.п. 2.1., 2.2. и 2.3. в столбце «Методы».

2.1. Аудиторные занятия (лекции, лабораторные, практические, семинарские)

1 семестр

Неделя	Кол. час	Вид занятия, тема и краткое содержание	Методы
		Лекция «Элементы теории множеств». Числа, постоянные, переменные, уравнения. Основные этапы и структура современной математики. Содержание курса высшей математики. Черты математического мышления; математические доказательства. Основные понятия и определения теории множеств. Операции над множествами, их свойства. Декартово произведение множеств.	М, Д
	Практическое занятие «Множества». Способы задания множеств: перечислением и описанием. Операции объединения и пересечения множеств их свойства. Разность множеств, дополнение множества. Декартово произведение множеств.	Э, И,Д
		Лекция «Матрицы и определители». Понятие матрицы. Различные виды матриц. Равенство матриц. Линейные операции над матрицами и их свойства. Произведение матриц и его свойства. Операция транспонирования, ее свойства. Понятие определителей 2-го, 3-го порядков. Основные свойства определителей.	М,Д
	Практическое занятие «Матрицы». Линейные операции над матрицами и их свойства. Произведение матриц и его свойства. Транспонирование матриц.	Э, И,Д
	Практическое занятие «Определители». Вычисление определителей 2-го, 3-го порядков. Свойства определителей.	Э,И,Д
		Лекция «Матрицы и определители». Понятие определителей n-го порядка. Теорема о разложении. Теорема аннулирования. Понятие миноров и алгебраических дополнений. Ранг матрицы. Элементарные преобразования матриц. Вычисление ранга матрицы с использованием элементарных преобразований. Определение обратной матрицы. Критерий существования обратной матрицы.	М,Д
	Практическое занятие «Матрицы и определители». Нахождение обратной матрицы с помощью транспонированной матрицы алгебраических дополнений. Выполнение проверки. Определение ранга матрицы.	Э, И,Д
		Лекция «Системы линейных уравнений». Основные определения: решение системы, совместные и несовместные, определенные и неопределенные, равносильные системы. Элементарные преобразования системы. Метод Жордана-Гаусса. Приведение системы к единичному базису. Свободные и базисные переменные. Общее, частное и базисное решения. Нахождение обратной матрицы методом Жордана-Гаусса. Модифицированные жордановы исключения. Применение МЖИ к решению линейных систем и нахождению базисных решений.	М, Д,ПБ
	Практическое занятие «Методы решения систем линейных уравнений». Решение линейных систем методом Жордана-Гаусса. Нахождение общего, частного и базисного решений. Нахождение обратной матрицы методом Жордана-Гаусса.	Э,И,Д
	Практическое занятие «Базисные решения систем линейных уравнений». Нахождение базисных решений систем линейных уравнений с помощью модифицированных жордановых исключений. Число базисных решений.	Э, И,Д
		Лекция «Системы линейных уравнений». Решение квадратных систем. Метод Крамера. Матричная форма записи системы линейных уравнений. Решение систем матричным способом. Решение матричных уравнений.	М, ПБ
	Практическое занятие «Решение линейных систем». Метод Крамера. Решение систем матричным способом.	Э, И,Д
		Лекция «Однородные системы уравнений». Определение однородной системы. Решение однородной системы. Условие существования ненулевых решений однородных систем.	М,Д ПБ
	Практическое занятие «Однородные системы». Решение однородных систем. Решение матричных уравнений. Контрольная работа.	Э, И,Д
	Практическое занятие «Балансовые модели». Линейная модель Леонтьева межотраслевого баланса. Коэффициенты прямых затрат. Матрица коэффициентов прямых затрат. Векторы выпуска и конечного продукта. Продуктивные модели. Матрица полных затрат. Критерий продуктивности.	М,Э, И,Д
		Лекция «Векторные пространства». Понятие n -мерного вектора. Линейные операции над n -мерными векторами. Пространство Rⁿ. Линейная комбинация векторов. Понятие линейной зависимости и независимости векторов. Существование в Rⁿ системы из n линейно независимых векторов. Линейная зависимость любых n +1 векторов Rⁿ..	М,Д, ПБ
	Практическое занятие «Векторные пространства.». Линейные операции над n -мерными векторами. Линейно зависимые и линейно независимые векторы. Выяснить является ли система векторов линейно зависимой или независимой, в случае линейной зависимости привести пример нетривиальной линейной комбинации, равной нулевому вектору.	Э, И
		Лекция «Базис векторного пространства». Понятие базиса в Rⁿ. Необходимое и достаточное условие того, что система векторов в Rⁿ образует базис. Разложение вектора пространства по базису. Координаты вектора в данном базисе. Переход к новому базису.	М,Д ПБ
	Практическое занятие «Базис пространства » Показать, что векторы образуют базис. Разложение любого вектора из Rⁿ по базису. Переход к новому базису.	Э, И
	Практическое занятие. Контрольная работа по методам решения систем линейных уравнений.	И
		Лекция «Линейные операторы и матрицы». Определение линейного оператора. Матрица линейного оператора в данном базисе. Зависимость между матрицами одного и того же оператора в разных базисах. Матричный оператор и его линейность. Примеры линейных операторов. Композиции матричных операторов. Ядро и образ линейного оператора. Изменение матрицы при переходе к новому базису. Операции над линейными операторами.	М,ПБ, Д
	Практическое занятие «Матричные операторы». Выяснить линейность операторов. Построить оператор по матрице и наоборот. Найти возможные композиции матричных операторов. Найти ядро и образ линейного оператора.	Э, И,Д
		Лекция «Комплексные числа и многочлены». Определение. Действия над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел. Алгебраические уравнения и многочлены. Теорема Гаусса.	М, ПБ, Д
	Практическое занятие «Матрица линейного оператора». Найти матрицу оператора в новом базисе. Выполнить операции над линейными операторами.	Э,И,Д
	Практическое занятие «Комплексные числа и многочлены» Действия над комплексными числами. Решение алгебраических уравнений в комплексной области.	Э,И,Д
		Лекция «Собственные векторы линейного оператора». Собственные значения и собственные векторы линейного оператора. Понятие характеристического уравнения линейного оператора или матрицы. Свойства собственные векторов и собственных значений линейного оператора. Теорема о свойствах собственных значений симметричной квадратной матрицы. Спектр линейного оператора.	М, Д, ПБ
	Практическое занятие «Собственные векторы и собственные значения». Нахождение собственных значений и собственных векторов линейного оператора, заданного матрицей. Приведение матрицы линейного оператора к диагональному виду.	Э,И,Д
		Лекция. «Евклидово пространство». Понятие скалярного произведения в Rⁿ. Свойства скалярного произведения. Эвклидово пространство. Норма (или длина) вектора. Неравенство Коши-Буняковского. Угол между векторам в Rⁿ. Ортогональные векторы. Ортонормированный базис в Rⁿ.	М, Д, ПБ
	Практическое занятие «Скалярное произведение» Скалярное произведение в Rⁿ. Свойства скалярного произведения. Норма (или длина) вектора. Неравенство Коши-Буняковского. Угол между векторами в Rⁿ. Ортогональные векторы. Ортонормированный базис в Rⁿ.	Д, И,Э
	Практическое занятие «Ортогонализация базиса евклидова пространства». В стандартном евклидовом пространстве ортонормировать систему векторов. Проверить ортогональность системы векторов и дополнить систему до ортогонального базиса.	Э,И,Д
		Лекция «Квадратичные формы». Определение квадратичной формы от п переменных и ее матричная запись. Понятие канонической квадратичной формы. Метод собственных векторов приведения квадратичной формы к каноническому виду. Понятие о положительно и отрицательно определенных квадратичных формах. Необходимое и достаточное условия существования положительно (отрицательно) определенной квадратичной формы. Критерий Сильвестра.	М,ПБ,Д
	Практическое занятие «Квадратичные формы». Привести квадратичную форму к каноническому виду, найти ортонормированный базис, в котором она имеет этот вид. Построить линии уровня квадратичной формы.	Э,И,Д
		Лекция «Элементы аналитической геометрии на плоскости». Понятие уравнения линии на плоскости Общее уравнение прямой. Частные виды уравнения прямой: уравнение прямой с угловым коэффициентом, по двум точкам, уравнение пучка прямых. Угол между прямыми. Условия параллельности и перпендикулярности.	М, ПБ, Д
	Практическое занятие «Уравнение прямой на плоскости». Составление уравнения прямой, проходящей через данную точку параллельно и перпендикулярно данной прямой. Нахождение расстояния между параллельными прямыми.	Э,И,Д
	Практическое занятие «Прямая линия в пространстве R²». Решение смешанных задач по теме.	Э,И,Д
		Лекция «Кривые 2-го порядка». Общее уравнение кривой 2-го порядка. Уравнение окружности. Каноническое уравнение эллипса, гиперболы, параболы. Приведение общего уравнения кривой 2-го порядка к каноническому виду. График дробно-линейной функции.	М, ПБ, Д
	Практическое занятие «Кривые 2-го порядка». Определение вида кривой 2-го порядка по ее общему уравнению. Построение кривой.	Э, И,Д
		Лекция «Элементы аналитической геометрии в пространстве 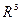.» Уравнение поверхности в пространстве. Общее уравнение плоскости в 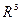. Вектор нормали. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей. Прямая в пространстве как линия пересечения двух плоскостей. Векторное уравнение прямой в пространстве, параметрические и канонические уравнения прямой в пространстве. Уравнение прямой, проходящей через две точки. Условия параллельности и перпендикулярности двух прямых в пространстве.	М, ПБ, Д
	Практическое занятие «Плоскость и прямая в пространстве». Исследование расположения плоскости по общему уравнению. Найти уравнение плоскости, проходящей: 1)через данную точку параллельно данной плоскости: 2) через две точки перпендикулярно данной плоскости: 3) через точку перпендикулярно двум плоскостям: 4) через три точки. Найти углы между плоскостями, указать среди них параллельные и ортогональные. Выяснить, определяет ли система уравнений прямую линию, если определяет. То найти параметрические уравнения. Написать уравнение прямой по двум данным точкам; точке и направляющем векторе.	Э,И,Д
	Практическое занятие «Плоскость и прямая в пространстве». Взаимное расположение прямой и плоскости в пространстве.	Э, И,Д
		Лекция «Выпуклые множества в ». Прямая и гиперплоскость в Rⁿ.Понятие полупространства. Внутренние и граничные точки множества. Выпуклое множество. Крайняя (угловая) точка. Теоремы о выпуклых множествах. Системы линейных неравенств: решение, допустимое решение, область допустимых решений, совместность, несовместность. Эквивалентные системы уравнений. Теорема о связи крайних точек области допустимых решений с опорными решениями эквивалентной системы уравнений.	М, ПБ, Д
	Практическое занятие «Системы линейных неравенств». Построение области допустимых решений.	Э,И,Д
		Лекция «Линейные задачи оптимизации». Линейные задачи оптимизации. Свойства решений линейных задач оптимизации. Графический способ решения задач линейной оптимизации.	М, ПБ, Д
	Практическое занятие «Линейные задачи оптимизации». Решение задач линейной оптимизации графическим способом.	Э,И,Д
	Практическое занятие. Контрольная работа по линейной алгебре и аналитической геометрии.	Э,И,Д

2 семестр

	Лекция «Числовые множества». Множество действительных чисел и их свойства. Числовая прямая. Промежутки действительных чисел. Абсолютная величина действительного числа и ее свойства. Окрестности точки, символов +µ, - µ, µ. Предельная точка множества. Ограниченные множества. Верхние и нижние грани числовых множеств. Теорема существования.	М,Д,Э
Практическое занятие «Числовые множества». Изучение материала на примерах и задачах. Нахождение верхней и нижней граней заданных множеств.	Э,И,Д
	Лекция «Отображения и функции». Отображение множеств. Образ и прообраз элемента, множества. Понятие функции, область определения, область значений. Способы задания функции. Постоянная функция. Монотонные функции. Ограниченные функции. Сложная функция. Обратная функция. Обратимость монотонной функции. Действия над числовыми функциями.	М, ПБ,П, Д
Практическое занятие «Отображения и функции». Отображение множеств. Образ и прообраз элемента, множества. Функции одной переменной. Нахождение области определения, множества значений.	Э,И,Д
Практическое занятие «Отображения и функции». Сложная функция. Взаимнооднозначное соответствие. Обратная функция. Действия над числовыми функциями. Основные элементарные функции и их графики. Классификация функций.	Э, И,Д
	Лекция «Числовые последовательности». Понятие числовой последовательности. Ограниченные и неограниченные последовательности. Монотонные последовательности. Предел последовательности. Геометрическая интерпретация предела последовательности. Сходящиеся последовательности, свойства. Теорема о пределе монотонной ограниченной последовательности. Число е	М, ПБ, П
Практическое занятие «Числовые последовательности». Числовые последовательности. Нахождение формулы общего члена последовательности. Примеры на доказательство монотонности и ограниченности заданных последовательностей. Нахождение пределов последовательностей по определению.	Э, И,Д
	Лекция «Предел функции». Два определения предела функции. Конечные и бесконечные пределы функций в конечных и бесконечных предельных точках. Геометрический смысл понятий предела. Приращение аргумента и приращение функции. Понятие непрерывности функции в точке: два определения и их равносильность. Односторонние пределы и односторонняя непрерывность. Свойства функции, имеющей конечный предел. Бесконечно малые, ограниченные и бесконечно большие функции и их свойства. Сравнение бесконечно малых функций. Понятие о неопределенностях.	М, ПБ
Практическое занятие «Предел последовательности и предел функции». Нахождение предела последовательности. Нахождение предела функции по определению.	Э,И,Д
Практическое занятие. Вычисление пределов функций.	И
	Лекция «Основные теоремы о пределах ». Основные теоремы о пределах: критерий существования конечного предела функции, теоремы о пределе суммы, произведения, частного; теорема о существовании предела сложной функции.	М, ПБ, П
Практическое занятие «Предел функции». Вычисление пределов, раскрытие неопределенностей.	И,Э,Д
	Лекция «Предельный переход в неравенствах ». Теоремы о предельном переходе в неравенствах. Первый замечательный предел. Второй замечательный предел.	М, ПБ, Д
Практическое занятие «Раскрытие различных видов неопределенностей». Раскрытие неопределенности ∞−∞. Раскрытие неопределенности .	И, Э,Д
Практическое занятие «Раскрытие различных видов неопределенностей». Вычисление пределов с помощью первого и второго замечательных пределов. Раскрытие различных видов неопределенностей.	И, Э,Д
	Лекция «Непрерывность функций». Непрерывность функции на множестве. Основные теоремы о непрерывных функциях: теорема о непрерывности суммы, произведения, частного непрерывных функций; теорема о непрерывности сложной функции; теорема о непрерывности элементарных функций. Точки разрыва. Классификация точек разрыва. Геометрическая иллюстрация точек разрыва.	М, ПБ, Д
Практическое занятие. «Непрерывность функций». Исследование функции на непрерывность. Односторонние пределы и односторонняя непрерывность.	И, Э,Д
	Лекция «Свойства функций непрерывных на отрезке ». Теорема Вейерштрасса, теорема Больцано, теорема о промежуточном значении непрерывной на отрезке функции.	М, ПБ, Д
Практическое занятие «Исследование функций на непрерывность». Исследование функции на непрерывность. Точки разрыва.	И, Э,д
Практическое занятие. Контрольная работа по теме «Предел и непрерывность функции».	М,И, Э,Д
	Лекция «Производная функции ». Понятие производной. Механический и геометрический смысл производной. Экономический смысл производной. Эластичность функции. Касательная и нормаль к кривой. Связь между непрерывностью и существованием производной.. Односторонние производные.	М, ПБ, Д
Практическое занятие «Производная функции». Нахождение производной функции по определению. Производные элементарных функций.	И, Э,Д
	Лекция «Правила нахождения производной». Производные суммы, произведения и частного двух функций. Производная сложной функции. Производная обратной функции.	М, ПБ, Д
Практическое занятие «Правила нахождения производных». Нахождение производных элементарных функций. Таблица производных. Нахождение производных с использованием основных правил дифференцирования.	М,И, Э,Д
Практическое занятие «Производная сложной функции». Нахождение производных сложных функций.	И, Э,Д
	Лекция «Производная неявной функции». Производная неявной функции. Производная степенно-показательной функции. Логарифмическое дифференцирование. Производные высших порядков.	М, ПБ, Д
Практическое занятие. «Примеры вычисления производных». Нахождение производных функций, заданных неявно. Нахождение производных функций с помощью логарифмического дифференцирования. Нахождение производных высших порядков.	И, Э,Д
	Лекция «Дифференциал функции» Понятие дифференциала функции и его геометрический смысл. Свойства дифференциала. Инвариантность формы дифференциала. Дифференциалы высших порядков.	М, ПБ, Д
Практическое занятие «Дифференциал функции». Нахождение дифференциалов. Таблица дифференциалов.	И, Э,Д
Практическое занятие. Применение дифференциалов к приближенным вычислениям.	И, Э,Д
	Лекция «Основные теоремы дифференциального исчисления». Теорема Ферма. Геометрический смысл теоремы Ферма. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа о конечных приращениях. Геометрический смысл теоремы Лагранжа. Теорема Коши. Правило Лопиталя.	М, ПБ, Д
Практическое занятие. «Правило Лопиталя.». Вычисление пределов с помощью правила Лопиталя.	И, Э,Д
	Лекция «Формула Тейлора». Формула Тейлора для многочлена. Разложение произвольной функции. Остаточный член в форме Лагранжа, Коши, Пеано. Формула Маклорена. Разложение некоторых элементарных функций по формуле Маклорена.	М, ПБ, Д
Практическое занятие «Формула Тейлора». Разложение функций по формуле Тейлора и Маклорена. Применение к приближенным вычислениям.	И, Э,Д
Практическое занятие. Контрольная работа по теме «Производная функции. Правило Лопиталя».	И, Э
	Лекция «Исследование функции с помощью производной». Монотонные функции. Теоремы о монотонных функциях. Понятие экстремума функции. Необходимые и достаточные условия экстремума.	М, ПБ, Д
Практическое занятие «Исследование функции». Исследование функций на монотонность и экстремумы.	И
	Лекция «Выпуклость и вогнутость графика функции». Понятие выпуклости и вогнутости графика функции. Достаточный признак выпуклости, вогнутости. Точки перегиба. Достаточное условие точки перегиба.	М, ПБ, Д, П
Практическое занятие. «Исследование функции». Нахождение наибольшего и наименьшего значений функции на замкнутом отрезке.	И, Э
Практическое занятие. «Исследование функции». Исследование функции на выпуклость и вогнутость, точки перегиба.	Э,И,Д
	Лекция «Полное исследование функции с помощью производной и построение графика». Асимптоты графика функции. Схема полного исследования функции.	М, ПБ, Д
Практическое занятие «Полное исследование функции». Примеры полного исследования функций и построение графиков.	И, Э, Д
	Лекция «Приложения производной. Задачи оптимизации». Эластичность функции. Предельная эффективность производства. Отыскание функции предельного дохода по функции среднего дохода. Задачи оптимизации. Основные понятия. Условия максимизации прибыли. Отыскание максимального выпуска. Коэффициенты кубической функции валовых издержек.	М, ПБ, Д
Практическое занятие. Экономические приложения производных. Решение задач.	И, Э, Д
Практическое занятие. Контрольная работа по теме «Исследование функции и приложения производных».	И

3 семестр

	Лекция «Интегральное исчисление. Неопределенный интеграл». Понятие первообразной функции. Теорема о первообразных. Неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица интегралов основных элементарных функций.	М,Д,Э
Практическое занятие «Неопределенный интеграл». Вычисление неопределенных интегралов методом разложения и подведением под знак дифференциала.	Э,И,Д
	Лекция «Основные методы интегрирования». Метод замены переменной в неопределенном интеграле. Метод интегрирования по частям в неопределенном интеграле.	М, ПБ,П, Д
Практическое занятие «Основные методы интегрирования». Вычисление неопределенных интегралов методом замены переменной.	Э,И,Д
Практическое занятие «Основные методы интегрирования». Вычисление неопределенных интегралов методом интегрирования по частям.	Э, И,Д
	Лекция «Частные методы вычисления неопределенных интегралов». Интегрирование рациональных функций. Интегрирование тригонометрических функций. Интегрирование некоторых иррациональных функций.	М, ПБ, П
Практическое занятие «Интегрирование рациональных функций». Вычисление неопределенных интегралов от рациональных функций.	Э, И,Д
	Лекция «Определенный интеграл». Задача о площади криволинейной трапеции. Интегральные суммы. Понятие определенного интеграла. Свойства определенного интеграла. Теорема существования определенного интеграла.	М, ПБ
Практическое занятие «Методы интегрирования». Нахождение неопределенных интегралов тригонометрических функций и некоторых иррациональных функций.	Э,И,Д
Практическое занятие «Методы интегрирования». Вычисление неопределенных интегралов различными методами. Самостоятельная работа.	И
	Лекция «Определенный интеграл с переменным верхним пределом ». Определенный интеграл с переменным верхним пределом. Теорема о его дифференцируемости. Формула Ньютона-Лейбница.	М, ПБ, П
Практическое занятие «Определенный интеграл». Вычисление определенных интегралов по формуле Ньютона-Лейбница.	И,Э,Д
	Лекция «Определенный интеграл ». Замена переменной в определенном интеграле. Интегрирование по частям в определенном интеграле	М, ПБ, Д
Практическое занятие «Примеры вычисления определенных интегралов». Вычисление определенных интегралов с помощью замены переменной.	И, Э,Д
Практическое занятие «Примеры вычислений определенных интегралов». Вычисление определенных интегралов с помощью метода интегрирования по частям.	И, Э,Д
	Лекция «Определенный интеграл». Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур и объемов тел вращения. Экономические приложения определенного интеграла.	М, ПБ, Д
Практическое занятие. «Приложения определенного интеграла». Вычисление площадей плоских фигур, ограниченных заданными линиями. Вычисление объемов тел вращения.	И, Э,Д
	Лекция «Несобственные интегралы ». Определение несобственных интегралов первого и второго рода. Сходимость. Критерий Коши. Признаки сходимости несобственных интегралов.	М, ПБ, Д
Практическое занятие «Несобственные интегралы». Вычисление несобственных интегралов.	И, Э,д
Практическое занятие «Несобственные интегралы». Исследовании на сходимость несобственных интегралов. Применение признаков сходимости.	М,И, Э,Д
	Лекция «Функции многих переменных ». Понятие n-мерного координатного и n-мерного евклидова пространства. Некоторые множества точек в . Окрестности точки. Понятие функции n-переменных, примеры. Область определения, множество значений. График функции. Поверхности и линии уровня.	М, ПБ, Д
Практическое занятие. Контрольная работа по теме «Интегральное исчисление».	И, Э,Д
	Лекция «Предел и непрерывность функции многих переменных». Предельная точка множества. Предел функции многих переменных. Понятие бесконечно малой, бесконечно большой, ограниченной функции многих переменных. Полное приращение функции многих переменных. Непрерывность функции многих переменных. Понятие замкнутого, ограниченного множества. Свойства функций непрерывных на замкнутом множестве.	М, ПБ, Д
Практическое занятие «Функции многих переменных». Примеры функций 2-х переменных. Нахождение области определения. Графики функции 2-х переменных. Построение линий уровня.	М,И, Э,Д
Практическое занятие «Предел и непрерывность». Вычисление пределов функции 2-х переменных. Исследование на непрерывность, точки и линии разрыва.	И, Э,Д
	Лекция «Частные производные». Частные приращения и частные производные функции многих переменных. Дифференцируемость функции многих переменных. Полный дифференциал. Понятие сложной функции. Непрерывность сложной функции. Теорема о производной сложной функции.	М, ПБ, Д
Практическое занятие. «Частные производные». Нахождение частных производных и полного дифференциала.	И, Э,Д
	Лекция «Частные производные высших порядков». Частные производные высших порядков. Теорема о равенстве смешанных частных производных второго порядка. Дифференциал второго порядка.	М, ПБ, Д
Практическое занятие «Частные производные». Примеры дифференцирования сложной функции.	И, Э,Д
Практическое занятие. Нахождения производных высших порядков. Нахождение дифференциала второго порядка для функции двух переменных .	И, Э,Д
	Лекция «Производная по направлению». Производная по направлению. Градиент функции многих переменных. Свойства градиента.	М, ПБ, Д
Практическое занятие «Производная по направлению». Задачи нахождения производной по направлению и градиента на примере функции двух переменных. Построение градиента и линии уровня.	И, Э,Д
	Лекция «Классические методы оптимизации». Понятие локального экстремума функции многих переменных. Необходимое условие локального экстремума. Достаточные условия локального экстремума.	М, ПБ, Д
Практическое занятие «Экстремум функции многих переменных». Решение задач на нахождение локальных экстремумов функций двух переменных.	И, Э,Д
Практическое занятие «Экстремум функции многих переменных». Исследование на экстремум функций двух и трех переменных.	И, Э
	Лекция «Условный экстремум». Понятие условного экстремума. Уравнения связи. Функция Лагранжа. Необходимые и достаточные условия существования условного экстремума.	М, ПБ, Д
Практическое занятие «Условный экстремум». Решение задач на нахождение условных экстремумов заданных функций.	И
	Лекция «Глобальный экстремум функции многих переменных». Понятие глобального экстремума функции многих переменных непрерывной в замкнутой, ограниченной области.	М, ПБ, Д, П
Практическое занятие. «Исследование функции многих переменных на экстремум». Нахождение наибольшего и наименьшего значений функции двух переменных в заданной области.	И, Э
Практическое занятие. Контрольная работа по теме «Функции многих переменных». .	Э,И,Д
	Лекция «Введение в теорию потребительского спроса». Функции спроса и предложения. Эластичность спроса. Рыночное равновесие. Функция полезности. Задача потребительского выбора. Кривые безразличия. Бюджетное ограничение. Решение задачи потребительского выбора и его свойства.	М, ПБ, Д
Практическое занятие «Функция спроса и предложения». Примеры функций спроса и предложения. Нахождение эластичности спроса. Рыночное равновесие.	И, Э, Д
	Лекция «Исследование модели потребительского выбора». Общая модель задачи потребительского выбора. Модель Р.Стоуна. Взаимозаменяемость благ. Эффект компенсации. Уравнение Слуцкого.	М, ПБ, Д
Практическое занятие «Задача потребительского выбора». Найти функции спроса при заданных ценах благ и доходе для различных функций предпочтения. Изобразить допустимые множества и кривые безразличия.	И, Э, Д
Практическое занятие. Решение и исследование задачи потребительского выбора.	И

4 семестр.

	Лекция «Введение в линейное программирование». Введение в линейное программирование. Примеры типовых задач. Задача оптимального планирования, задача о диете. Модели линейного программирования с двумя переменными.	М,Д,Э
Практическое занятие «Построение моделей задач ЛП». Построение простейших моделей задач ЛП с двумя переменными. Решение графическим способом.	Э,И,Д
	Лекция «Теоретические основы методов линейного программирования». Математическая постановка задач линейного программирования. Основные определения. Различные формы задач ЛП: общая, стандартная и каноническая. Переход от одной формы задачи ЛП к другой. Запись задач ЛП в матричной форме. Свойство решений задач ЛП. Фундаментальная теорема.	М, ПБ,П, Д
Практическое занятие «Построение моделей и решение задач ЛП». Модели экономических задач ЛП.	Э,И,Д
Практическое занятие «Свойства решений задач ЛП.». Метод перебора вершин многоугольника допустимых решений. Случаи неразрешимости задачи ЛП.	Э, И,Д
	Лекция «Симплекс-метод решения задачи ЛП». Идея симплекс-метода. Симплекс-таблицы. Симплексные отношения. Переход от одного опорного плана к другому. Критерий оптимальности опорного плана задачи ЛП.	М, ПБ, П
Практическое занятие «Решение задачи ЛП симплекс-методом». Приведение задачи ЛП к стандартной форме и каноническому виду. Запись канонической задачи в симплекс-таблицу. Правило выбора разрешающего столбца и разрешающей строки	Э, И,Д
	Лекция «Симплекс-метод». Условия неограниченности целевой функции. Условия улучшения опорного плана. Алгоритм симплексного метода. Понятие зацикливания в случае вырожденности опорного плана.	М, ПБ
Практическое занятие «Решение задачи ЛП симплекс-методом». Решение задачи ЛП, когда свободные члены системы ограничений положительны. Решение задачи об оптимальном планировании производства симплекс-методом. Экономический анализ решения. Решение задачи ЛП, когда среди свободных членов системы ограничений есть отрицательные.	Э,И,Д
Практическое занятие. Решение общей задачи ЛП. Особенности приведения системы ограничений к единичному базису. Алгоритм решения общей задачи ЛП.	И
	Лекция «Элементы теории двойственности ». Понятие о двойственных задачах линейного программирования. Прямая и двойственная задачи. Экономический смысл двойственных переменных. Симметричные двойственные задачи. Правила построения двойственной задачи. Связь между решениями прямой и двойственной задач. Основное неравенство двойственности. Экономическая интерпретация.	М, ПБ, П
Практическое занятие «Двойственные задачи». Примеры построения двойственных задач. Построение двойственной задачи об оценивании ресурсов на примере задачи оптимального планирования. Решение обеих задач. Анализ полученных решений.	И,Э,Д
	Лекция «Основные теоремы двойственности ». Первая теорема двойственности. Экономическая интерпретация. Двойственные симплекс-таблицы. Вторая теорема двойственности. Экономическая и геометрическая интерпретация. Анализ устойчивости двойственных оценок. Понятие о несимметричных двойственных задачах.	М, ПБ, Д
Практическое занятие «Двойственные задачи и их решение по теоремам двойственности». Решение симметричных двойственных задач с помощью двойственных симплекс таблиц.	И, Э,Д
Практическое занятие. Нахождение и исследование решений двойственных задач по второй теореме двойственности.	И, Э,Д
	Лекция «Транспортная задача (ТЗ)». Содержательная постановка ТЗ. Математическая модель ТЗ. Критерий разрешимости ТЗ. Ранг матрицы ТЗ. Закрытая модель ТЗ. Открытая модель ТЗ. Вырожденный и невырожденный опорный план. Определение исходного опорного плана. Метод «северо-западного угла». Метод «наименьшей стоимости».	М, ПБ, Д
Практическое занятие «Методы построения исходного опорного плана ТЗ». Построение математической модели ТЗ. Проверка критерия разрешимости ТЗ. Транспортная задача с нарушенным балансом производства и потребления. Построение исходных опорных планов методом «северо-западного угла» и методом «наименьшей стоимости». Проверка построенного плана на невырожденность.	И, Э,Д
	Лекция «Определение оптимального плана ТЗ. Метод потенциалов ». Понятие цикла. Переход от одного опорного плана к другому сдвигом по циклу пересчета. Достаточные условия оптимальности опорного плана ТЗ. Построение системы потенциалов. Алгоритм решения ТЗ методом потенциалов.	М, ПБ, Д
Практическое занятие «Решение ТЗ методом потенциалов». Решение транспортных задач с невырожденным и вырожденным опорным планом методом потенциалов. Экономический анализ полученного решения. Решение транспортной задачи с нарушенным балансом.	И, Э,д
Практическое занятие. Контрольная работа по теме «Симплекс-метод. Транспортная задача».	М,И, Э,Д
	Лекция «Элементы теории игр ». Предмет и основные понятия теории игр: стратегия, оптимальная стратегия, платежная матрица. Классификация игры. Игры двух лиц с нулевой суммой. Смешанная и чистая стратегии, функция выигрыша, седловой элемент платежной матрицы, цена игры. Понятие об игре, разрешимой в чистых стратегиях. Максиминные и минимаксные стратегии игроков. Теорема о разрешимости игры в чистых стратегиях.	М, ПБ, Д
Практическое занятие «Матричные игры двух лиц с нулевой суммой, разрешимых в чистых стратегиях». Нахождение оптимальных стратегий игроков для игры, разрешимой в чистых стратегиях, а также цены игры. Задачи с экономическим содержанием.	И, Э,Д
	Лекция «Решение матричных игр в смешанных стратегиях». Смешанные стратегии. Функция выигрыша (платежная функция). Оптимальные стратегии. Теорема Неймана. Решение матричных игр 2×2, m×2, 2×n. Свойства оптимальных решений. Геометрическая интерпретация.	М, ПБ, Д
Практическое занятие «Решение матричных игр в смешанных стратегиях». Вычисление значений платежной функции. Решение матричных игр 2×2, m×2, 2×n графическим методом.	М,И, Э,Д
Практическое занятие «Решение матричных игр в смешанных стратегиях». Упрощение платежной матрицы. Принцип доминирования.	И, Э,Д
	Лекция «Матричные игры двух лиц с нулевой суммой, разрешимые в смешанных стратегиях». Сведение матричной игры к паре двойственных задач линейного программирования.	М, ПБ, Д
Практическое занятие. «Решение матричных игр». Сведение матричной игры к паре двойственных задач линейного программирования и ее решение с помощью двойственных симплекс-таблиц.	И, Э,Д
	Лекция «Дискретное программирование». Предмет дискретного программирования. Классификация математических моделей и прикладных задач дискретного программирования. Задача целочисленного линейного программирования. Постановка задачи. Экономическая и геометрическая интерпретация. Определение оптимального плана задачи целочисленного программирования. Метод отсечения. Идея метода правильного отсечения. Алгоритм Гомори, реализующий метод правильного отсечения.	М, ПБ, Д
Контрольная работа по матричным играм.	И, Э,Д
Практическое занятие «Задача целочисленного программирования». Построение моделей. Графический метод решения. Решение задачи целочисленного программирования методом Гомори. .	И, Э,Д
	Лекция «Комбинаторные методы дискретного программирования». Комбинаторные методы дискретного программирования. Метод ветвей и границ.	М, ПБ, Д
Практическое занятие «Метод ветвей и границ». Решение задачи о коммивояжере методом ветвей и границ.	И, Э,Д
	Лекция «Нелинейное программирование». Постановка задачи нелинейного программирования. Экономическая и геометрическая интерпретация. Решение методом множителей Лагранжа.	М, ПБ, Д
Практическое занятие «Нелинейное программирование». Нахождение решения задач нелинейного программирования с использованием ее геометрической интерпретации.	И, Э,Д
Практическое занятие. Решение задач методом множителей Лагранжа.	И, Э
	Лекция «Нелинейное программирование». Задачи нелинейного программирования при ограничениях-неравенствах. Теорема Куна-Таккера. Седловая точка. Квадратичное программирование.	М, ПБ, Д
Практическое занятие. Решение задачи квадратичного программирования. .	И
	Лекция «Динамическое программирование». Общая характеристика задач динамического программирования и их геометрическая и экономическая интерпретация. Метод динамического программирования. Принцип оптимальности Беллмана. Функциональное уравнение Беллмана.	М, ПБ, Д, П
Практическое занятие. «Динамическое программирование». Решение задачи об оптимальном распределении ресурсов.	И, Э
Практическое занятие. Задача об оптимальном распределении средств на расширение и модернизацию производства и ее решение методом динамического программирования. .	Э,И,Д
	Лекция «Метод динамического программирования». Задача об оптимальном распределении инвестиций между предприятиями Задача о замене оборудования.	М, ПБ, Д
Практическое занятие «Решение задач методом динамического программирования». .Решение задачи об использовании оборудования. Решение задачи об оптимальном распределении капиталовложений между двумя предприятиями в течение N лет.	И, Э, Д
	Лекция «Программирование на сетях». Понятие графа. Способы задания. Сети. Потоки в сетях. Постановка задачи о нахождении максимального потока в сети. Алгоритм Форда-Фалкерсона нахождения максимального потока. Задача нахождения кратчайшего пути в сети и потока наименьшей стоимости.	М, ПБ, Д
Практическое занятие. Решение задачи нахождения максимального потока в сети. Алгоритм Форда–Фалкерсона.	И, Э, Д
Практическое занятие. Решение задачи нахождения кратчайшего пути в сети.	И

2.2. Индивидуальная работа преподавателя со студентом

1 семестр

Неделя	Кол. час	Темы, разделы, вынесенные на индивидуальную подготовку, по докладам на НОК, рефератам, темы контрольных работ, промежуточный контроль уровня усвоения дисциплины и др.	Методы
		Консультация по теме «Элементы теории множеств. Отображения множеств».	Д, И
		Свойства определителей. Приемы вычисления определителей n-го порядка. Консультация.	Д, И
		Обратная матрица. Теорема существования и единственности. Тестирование по теме «Матрицы и определители».	Д, И
		Консультация по методам решения систем линейных уравнений.	Д, И
		Индивидуальная домашняя работа по методам решения систем линейных уравнений.	Д, И
		Векторные пространства. Линейная зависимость векторов. Базис векторного пространства, разложение по базису. Самостоятельная аудиторная работа.	Д, И
		Линейные операторы. Нахождение матрицы линейного оператора в данном базисе. Зависимость между матрицами одного и того же оператора в разных базисах. Вывод формулы.	Д, И
		Комплексные числа. Тригонометрическая форма комплексного числа.	Д, И
		Собственные векторы и собственные значения линейного оператора. Линейная модель обмена (модель международной торговли).	Д, И
		Алгоритм построения ортонормированного базиса в евклидовом пространстве.	Д, И
		Кривые 2-го порядка. Приведение общего уравнения кривой второго порядка к каноническому виду.	Д, И
		Контрольная работа по линейной алгебре и аналитической геометрии.	Д, И
		Консультация перед экзаменом.	Д, И

2 семестр

Неделя	Кол. час	Темы, разделы, вынесенные на индивидуальную подготовку, по докладам на НОК, рефератам, темы контрольных работ, промежуточный контроль уровня усвоения дисциплины и др.	Методы
4-5		Консультация по теме «Предел числовой последовательности и предел функции».	И
		Исследование на непрерывность заданных функций.	И
		Контрольная работа «Пределы и непрерывность».	И
9-11		Производная функции. Вывод формул производных некоторых элементарных функций	И
		Контрольная работа по теме «Производная функции. Правило Лопиталя».	И,
		Индивидуальная работа «Полное исследование заданной функции и построение графика».	И, Э
		Консультация перед зачетом.	И

3семестр

Неделя	Кол. час	Темы, разделы, вынесенные на индивидуальную подготовку, по докладам на НОК, рефератам, темы контрольных работ, промежуточный контроль уровня усвоения дисциплины и др.	Методы
4,5		Консультация по методам интегрирования.	И
		Реферат на тему «Экономические приложения определенного интеграла».	И
		Контрольная работа по интегральному исчислению.	И
		Консультация по теме «Функция многих переменных».	И, Э
		. Консультация по темам докладов на НОК.
		Индивидуальная домашняя работа «Исследование функции двух переменных на экстремум. Условный экстремум».	И
		Студенческая конференция «Математика в экономике».	И, Э

12 Следующая ⇒

Поделиться с друзьями:

Дата добавления: 2016-03-27; Мы поможем в написании ваших работ!; просмотров: 290 | Нарушение авторских прав

Поиск на сайте:

Лучшие изречения:

Вы никогда не пересечете океан, если не наберетесь мужества потерять берег из виду. © Христофор Колумб
==> читать все изречения...

2309 -

| 2124 -