Методические указания к задаче 2

С материалом по основным характеристикам случайных процессов можно ознакомиться в [1- с.49-52; 2- с.43-44; 4- с.138-139, 149-151; 6- с.20-22].

Согласно исходным данным значение ФПВ вне интервала [a, b] равно нулю. δ(х-х₀) – дельта-функция. При х = х₀, δ(0) = ∞, при х ≠ х₀, δ(х-х₀) = 0. Если случайный процесс принимает значение х₀ с вероятностью р₀, то ФПВ в качестве одной из составляющих содержит дельта- функцию: р₀∙δ(х-х₀).

Вычислить значение h ФПВ можно используя условие нормировки плотности вероятности (2.1 а) с учетом условия нормировки для дельта- функции (3.1 б):

а). ∫р(х)dx =1; б). ∫δ(х-х₀)dх = 1. (2.1)

Взяв интеграл от ФПВ, из равенства (2.1 а) можно определить h.

ФРВ случайного процесса связана с ФПВ соотношением:

F(х) = ∫р(ν)dν. (2.2)

Определение ФРВ следует проводить по участкам: -∞<х<a, a≤x<c, x=c, c≤x< d, x=d, d≤x<b, x=b, x≥b. Исходя из свойств ФРВ ее значение для х=b и х>b должно равняться: F(b)=F(х>b)=1.

При нахождении М(х) и D(х) следует учитывать фильтрующее свойство дельта- функции:

 

∫f(x)∙δ(х-х₀)dx = f(x₀). (2.3)

М(х) = ∫x∙p(x)dx.; D(х) = ∫[x - M(x)]²∙p(x)dx.. (2.4)

Рассчитать дисперсию D(x) можно также через М(х²):

М(х²) = ∫х²∙р(х)dx. (2.5)

D(х) = М(х²) – [М(х)]². (2.6)

В литературе встречаются разные обозначения математического ожидания и дисперсии: М(х) или m_x, m₁, M{X(t)}, Х; D(x) или σ², D{X(t)}, [Х-Х]²; M(x²) или m₂, M{X²(t)}, X².

Задача 3

 

Вольт-амперная характеристика (ВАХ) биполярного транзистора амплитудного модулятора аппроксимирована выражением:

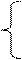S · (u_б – Е₀), при u_б ≥ Е₀;

i_к =

0, при u_б < Е₀;

где: i_к – ток коллектора транзистора, мА;

u_б – напряжение на базе транзистора, В;

S – крутизна характеристики (ВАХ), мА/В;

Е₀ – напряжение отсечки, В.

Требуется:

1. Пояснить назначение модуляции несущего сигнала и кратко описать различные виды аналоговой модуляции.

2. Изобразить упрощенную схему транзисторного амплитудного модулятора, описать принцип его работы и назначение элементов схемы.

3. Дать определение статической модуляционной характеристики (СМХ), рассчитать и построить СМХ при заданных S, Е₀ и значении амплитуды несущего ВЧ сигнала U_m.

4. С помощью СМХ определить оптимальное напряжение смещения на базу транзистора Е_бопт. и допустимую величину амплитуды U_{Ω макс.} модулирующего сигнала u_мод.(t) = U_Ω∙cosΩt, соответствующие неискаженной модуляции. Здесь Ω=2πF.

5. Рассчитать коэффициент модуляции М для выбранного режима и построить временную, спектральную и векторную диаграммы однотонального АМ сигнала. Записать математическое выражение этого сигнала.

Значения S, Е₀, U_m, ƒ₀ и F приведены в таблице 4.

 

Таблица 4

Последняя цифра номера варианта
S, мА/В
ƒ0, кГц
Предпоследняя цифра номера варианта
Е0, В	0,35	0,45	0,55	0,65	0,75	0,4	0,5	0,6	0,7	0,8
Um, В	0,4	0,5	0,45	0,6	0,8	0,45	0,35	0,5	0,55	0,65
F, кГц	3,4				5,5		4,4	6,5

 

Методические указания к задаче 3.

 

Материал по амплитудной модуляции можно изучить в [1- с.88-91; 2- с.57-60; 4- с.88-90, 93-94]. Схема транзисторного амплитудного модулятора приводится в [1- с.94, рисунок 3.14; 4- с.283]. Расчет СМХ следует проводить после ознакомления с [1- с.85-88, 94-95; 2- с.84, 87-88; 4- с.269, 272-273, пример 11.2, 283-484, пример 11.4].

Под СМХ понимается зависимость амплитуды первой гармоники тока коллектора от напряжения смещения на базе транзистора, при постоянной амплитуде напряжения несущего колебания: I_к1(Е_б)│_Um=const. [1- с.94].

Расчет СМХ следует провести для пяти - семи значений напряжения смещения Е_б на интервале от (Е₀ – U_m) до (Е₀ + U_m), в пределах которого угол отсечки изменяется от 0⁰ до 180⁰ (от 0 до π радиан). Для значения Е_б и заданных Е₀ и U_m определяется угол отсечки θ (11.14) [4- с.272]:

θ = arccos[(Е₀ – E_б)/ U_m], рад.. (3.1)

C помощью θ определяется значение амплитуды первой гармоники тока коллектора I_к1 (11.15) [4- с.273, пример 11.2]:

I_к1 = S∙U_m∙γ₁(θ), мА (3.2)

где: γ₁(θ) – коэффициент Берга.

Значения коэффициентов Берга можно определить по графику рисунок 4.10 [2], таблице [4- с.443], где θ в градусах, или рассчитать по формулам, приведенным в приложении к методическим указаниям, где θ – в радианах.

Для неискаженной модуляции необходима работа на линейном участке СМХ. Оптимальное напряжение смещения Е_бопт. лежит на середине линейного участка СМХ, а допустимая величина амплитуды модулирующего напряжения U_Ωмакс. выбирается так, чтобы напряжение на базе транзистора не выходило за пределы линейного участка СМХ.

Коэффициент модуляции определяется по СМХ для выбранного режима:

М = (I_{к1 макс.} - I_{к1 мин.}) / (I_{к1 макс.} + I_{к1 мин.}), (3.3)

где: I_{к1 макс.} и I_{к1 мин.} – максимальное и минимальное значения тока I_к1 по СМХ для Е_бмакс. и Е_бмин.

 

Задача 4

 

Вольт-амперная характеристика (ВАХ) диода амплитудного детектора аппроксимирована выражением:

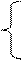S∙u, при u ≥ 0;

i_д =

0, при u < 0;

где: i_д – ток диода;

S – крутизна характеристики (ВАХ);

u – напряжение на диоде.

На вход детектора воздействует однотональный АМ сигнал:

u_АМ(t) = U_m∙[1 + М∙cos(2π∙F∙ t)] ∙ cos (2π∙ƒ₀∙ t), В

где: U_m – амплитуда несущего сигнала, В;

М – коэффициент модуляции;

F – частота модулирующего сигнала, Гц;

ƒ₀ – частота несущего сигнала, Гц.

Требуется:

1. Пояснить назначение детектирования модулированных колебаний. Изобразить упрощенную схему диодного детектора, описать принцип его работы и назначение элементов схемы.

2. Рассчитать необходимое значение сопротивления нагрузки детектора R_н, для получения заданного значения коэффициента передачи детектора к_д.

3. Выбрать значение емкости нагрузки детектора С_н при заданных ƒ₀ и F.

4. Рассчитать и построить временную, спектральную и векторную диаграммы напряжений на входе и выходе детектора.

Значения S, U_m, М, F, ƒ₀ и к_д приведены в таблице 5.

 

Таблица 5

Последняя цифра номера варианта
S, мА/В
М	0,8	0,85	0,9	0,7	0,75	0,5	0,55	0,6	0,65	0,7
F, кГц	3,4				5,5		4,5	6,5
Предпоследняя цифра номера варианта
Um, В	1,0	1,2	1,4	1,6	1,8	1,1	1,3	1,5	1,7	1,9
ƒ0, кГц
кд	0,9	0,7	0,85	0,6	0,8	0,65	0,75	0,8	0,6	0,7

 

Методические указания к задаче 4.

 

Принцип детектирования АМ колебаний и работа амплитудного детектора описаны в [1- с.95-96; 4- с.286-290], схема амплитудного детектора изображена в [4- с.289], расчет схемы детектора приведен в [4- с.286-290, пример 11.5].

Для расчета R_н следует воспользоваться выражениями для к_д и (11.58) в [4]:

к_д = cos θ; tg θ – θ = π / (S∙R_н), (4.1)

где: θ – угол отсечки в радианах.

Для нормальной работы диода необходимо, чтобы сопротивление нагрузки R_н значительно превышало сопротивление диода в открытом состоянии:

R_н >> r_i = 1/S, то есть R_н∙ S >> 1 (4.2)

Кроме этого, для того чтобы нагрузочная R_нC_н цепочка выполняла функции ФНЧ и подавляла ВЧ составляющие, выделяя НЧ составляющую, необходимо выполнение условий (11.51) в [4]:

1/(2π∙ƒ₀∙Rн) << С_н << 1/(2π∙F∙R_н ). (4.3)

Из этого соотношения выбирается значение емкости нагрузки С_н, удовлетворяющее этому неравенству.

Выходное напряжение детектора содержит две составляющие: постоянную составляющую и полезную НЧ составляющую с частотой F, выделяемые ФНЧ нагрузочной R_нC_н цепочкой):

U_вых.(t) = I₀(t)∙R_н = S∙U(t)∙γ₀(θ)∙R_н, В (4.4)

где: I₀(t) – постоянная составляющая (нулевая гармоника) выходного тока;

U(t) – огибающая АМ колебания на входе детектора;

γ₀(θ) – коэффициент Берга; его нахождение смотри в методических указаниях к задаче 3.

U(t) = U_m[1+М∙cos(2π∙F∙t)], В. (4.5)

 

 

Задача 5

Задано модулирующее напряжение (сигнал):

U_мод.(t) = U_F∙cos(2π∙F∙ t), В

где: U_F – амплитуда модулирующего сигнала, В;

F – частота модулирующего сигнала, Гц.

Требуется:

1. Привести математические выражения для модулированных напряжений

(сигналов) при однотональных частотной (ЧМ) и фазовой (ФМ) модуляциях.

Пояснить различие между ЧМ и ФМ.

2. Построить спектральную диаграмму сигнала с однотональной угловой модуляцией (УМ) при заданных значениях девиации фазы ∆φ_д (для ФМ) или девиации частоты ∆ƒ_д (для ЧМ) и частот несущего ƒ₀ и модулирующего F сигналов. Амплитуда несущего сигнала U_m = 10 В. Определить практическую ширину спектра модулированного сигнала.

3. Построить спектральные диаграммы однотональных ЧМ и ФМ сигналов при увеличении частоты модулирующего сигнала F в n раз. Определить, как изменятся при этом параметры ЧМ и ФМ сигналов, их спектральные диаграммы и ширина спектров. В каком случае спектры ЧМ и ФМ сигналов будут совпадать?

Значения ƒ₀, F, ∆φ_д, ∆ƒ_д и n приведены в таблице 6.

Таблица 6

Последняя цифра номера варианта
∆φд, рад	0,4	0,8	1,2	1,6
F, кГц
∆ƒд, кГц
Предпоследняя цифра номера варианта
ƒ0, кГц
n

 

Методические указания к задаче 5.

 

С материалом по угловой модуляции (ЧМ и ФМ) можно ознакомиться в литературе [1- c.96-99; 2- с.64-70; 4- с.96-103; 6- с.78-81, 91-93].

Следует разобраться в различиях между ЧМ и ФМ, уяснить смысл основных параметров модуляции, от чего они зависят, каково их максимальное значение. Отдельно следует разобраться со спектром сигналов угловой модуляции, его структурой, определением реальной ширины спектра. Эти вопросы хорошо и доступно изложены в [2] и [4]. Проработайте примеры 3.3 в [2] и 4.2 в [4].

Общие математические выражения и для однотональных сигналов с УМ приводятся в (3.13), (3.15), (3.16) [2] и в (4.20), (4.24), (4.26) [4].

Спектральное разложение сигналов с УМ приводится в (3.19) [2- с.67-68] и (4.32) [4- с.100]. Разберите пример 3.4, рисунки 3.10 и 3.11, таблицу 3.3 [2] и пример 4.3, рисунок 4.8, таблицу 4.1 [4].

Амплитуда каждой составляющей спектра определяется как:

U_к = U_m∙J_к(m), В (5.1)

где: J_к(m)–значение функции Бесселя первого рода, к- го порядка от аргумента m.

Значения функции Бесселя можно найти по графику на рисунке 3.10 [2], по таблице 4.1 [4], в математическом справочнике [13], или по таблицам П.3- П.5 в приложении к методическим указаниям. При определении функций Бесселя существует рекуррентная формула для нахождения ее значений, не отображенных на графиках и в таблицах:

J_к+1(m) = (2к/m)∙J_к(m) – J_к-1(m). (5.2)

Следует учитывать, что для четных боковых составляющих (к = 2, 4,...)

J_-к(m)=J_к(m), а для нечетных боковых составляющих (к=1, 3,...) J_-к(m)=-J_к(m).

Следовательно, начальные фазы боковых составляющих с частотами ƒ₀ + к∙F и

ƒ₀ - к∙F совпадают, если к- четное число, и отличаются на 180⁰ (π радиан) если

к- нечетное число.

При определении практической ширины спектра можно пренебречь спектральными составляющими с амплитудами, меньшими чем (2–5)% от амплитуды несущего сигнала U_m. Тогда практическая ширина спектра при угловой модуляции (ЧМ и ФМ), определяется числом гармонических составляющих, которое независимо от частоты модуляции равно [2, 4]:

- при m < 0,6 N = 2 + 1 = 3, (5.3)

- при m =0,6-10 N = 2∙(m+1) + 1, (5.4)

- при m > 10 N = 2m + 1. (5.5)

Здесь m- индекс модуляции

В задаче, при определении ширины спектра, следует ограничиться составляющими с амплитудами до 2 % от амплитуды несущей (до U_к ≥ 0,02∙U_m, то есть до J_к(m) ≥ 0,02).

 

Задача 6

 

Объем алфавита источника дискретных сообщений составляет К знаков, кодируемых кодовыми комбинациями равномерного двоичного кода. Вероятности появления элемента (символа) «1» на информационных позициях (в разрядах) кодовой комбинации знака- р_i(1). Здесь i – номер единичного элемента (позиции, разряда) в кодовой комбинации (слева направо).

Передача информации ведется по дискретному двоичному каналу без помех. Скорость передачи составляет N знак/мин.

Требуется:

1 Дать определение единицам измерения «бит», «бит/с», «Бод».

2 Определить энтропию (среднее количество информации) каждого

элемента кодовой комбинации Н_эл.i, бит/эл и энтропию знака (кодовой комбинации) Н_зн., бит/знак.

1. Определить максимально возможные значения энтропии элемента

Н_{эл. макс.} и знака Н_{зн. макс.}, а также коэффициент избыточности источника ǽ.

4. Определить скорости модуляции В, Бод и передачи информации R, бит/с

5. Составить кодовую комбинацию двоичного кода номера своего варианта соответствующую параметрам источника и определить количество информации I_к.к. содержащееся в ней.

Значения К, N, р_i(1) приведены в таблице 7.

 

Таблица 7

Последняя цифра номера варианта
К
р1(1)	0,25	0,55	0,65	0,4	0,3	0,6	0,25	0,65	0,35	0,5
р2(1)	0,3	0,4	0,45	0,6	0,6	0,2	0,6	0,7	0,65	0,2
р3(1)	0,35	0,35	0,4	0,55	0,7	0,3	0,35	0,2	0,5	0,35
Предпоследняя цифра номера варианта
N, знак/мин
р4(1)	0,4	0,8	0,75	0,35	0,25	0,45	0,45	0,4	0,8	0,45
р5(1)	0,45	0,7	0,65	0,45	0,8	0,35	0,5	0,5	0,4	0,4
р6(1)	0,05	0,15	0,25	0,35	0,45	0,55	0,65	0,75	0,85	0,95
р7(1)	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,5