Материал по корреляционной теории стационарных случайных процессов

Задача 1

Энергетический спектр нормального (гауссовского) стационарного случайного процесса Х(t) равен W(w). Cреднее значение случайного процесса равно m.

Требуется:

1. Определить корреляционную функцию В(t) случайного процесса.

2. Построить графики W(w) и В(t) с указанием масштаба по осям.

3. Определить эффективную ширину энергетического спектра ∆ω_э и интервал корреляции τ_к случайного процесса.

4. Записать математическое выражение и построить график функции плотности вероятности р(х) мгновенных значений случайного процесса.

5. Определить вероятность того, что мгновенные значения случайного процесса будут находиться внутри интервала (c, d ] - Ρ(c < x ≤ d).

Исходные данные к задаче приведены в таблицах 1 и 2.

Таблица 1

Последняя цифра номера варианта	Энергетический спектр W(ω)
	W(ω) = W0∙ω/α, при 0 ≤ ω ≤ α; W(ω) = 0, при ω > α;
	W(ω) = W0∙ (1- ω/α), при 0 ≤ ω ≤ α; W(ω) = 0, при ω > α;
	W(ω) = W0∙α2 / (α2+ω2);
	W(ω) = W0∙exp[- ω2/α2];
	W(ω) = W0, при 0 ≤ ω ≤ α; W(ω) = 0, при ω > α;
	W(ω) = W0, при ω0 ≤ ω ≤ ω0+α; ω 0 = 103∙α; W(ω) = 0, при ω < ω0, ω > ω0 + α;
	W(ω) = W0∙ (ω- ω0)/α, при ω0 ≤ ω ≤ ω0+α; ω 0 = 103∙α; W(ω) = 0, при ω < ω0, ω > ω0+α;
	W(ω) = W0∙[1 – (ω – ω0)/α], при ω0 ≤ ω ≤ ω0+α; ω0 = 103∙α; W(ω) = 0, при ω < ω0, ω > ω0+α;
	W(ω) = W0∙α2/[α2 + (ω - ω0)2]; ω 0 = 103∙α;
	W(ω) = W0∙exp[- (ω - ω0)2/α2]; ω 0=103∙α;

 

Таблица 2

Предпоследняя цифра номера варианта
W0, В2∙с/рад	2∙10-1	10-3	5∙10-2	10-2	4∙10-3	3∙10	6∙10-1	2∙10-4	0,4	2
α, рад/с
mх , B						-1	-2	-3	-4
c, B	-1	-2				-2,5	-3	-4	-5,5	-2
d, B	2,5						-0,5	-1,5	-2	1,5

 

Методические указания к задаче 1.

Материал по корреляционной теории стационарных случайных процессов

изложен в [1- с.52-53, 56-59; 2- с.46-47; 4- с.140-141, 160-164]. Более полный

материал по задаче можно найти в [4].

Энергетический спектр случайного процесса W(ω) связан с функцией корреляции В(τ) парой преобразований Фурье:

 

В(τ) = 1/(2π)∙∫ W(ω)∙exp(jωτ)∙dω;

W(ω) = ∫ В(τ)∙exp(-jωτ)∙dτ; (1.1)

Поскольку В(τ) – четная функция, то соответствующий спектр мощности W(ω) представляет собой четную функцию частоты ω. Отсюда следует, что пару преобразований Фурье можно записать, используя лишь интегралы в полубесконечных пределах:

В(τ) = 1/π ∙ ∫ W(ω) ∙ cos(ωτ)∙dω;

W(ω) = 2 ∙ ∫ В(τ) ∙ cos(ωτ)∙dτ; (1.2)

При этом, если энергетический спектр процесса W(ω) отличен от нуля в конечной полосе частот, в качестве пределов интегрирования в формуле (1.2) берутся границы энергетического спектра. В [4- с.161-162] приводится ряд примеров вычисления корреляционных функций случайных процессов.

Для низкочастотного процесса (ω₀=0) в вариантах 0–4 (таблица 1), в формулу В(τ) следует подставлять заданный в таблице W(ω). У НЧ процессов функцию корреляции нередко обозначают В₀(τ).

Для высокочастотного процесса (ω₀>>α) в вариантах 5–9 функция корреляции имеет вид [4- с.171-172]:

В(τ) = В₀(τ) ∙ cos(ω₀τ), (1.3)

где: В₀(τ) – функция корреляции огибающей (НЧ процесса).

При этом, при определении В(τ), в формуле Винера-Хинчина (1.2) следует сделать замену переменной ω=ω₀+Ω (ω-ω₀=Ω) и интегрирование производить по переменной Ω на интервале от 0 до ∞, используя формулу тригонометрического преобразования (см. приложение к методуказаниям):

В(τ) = 1/π ∙ ∫ W(ω- ω₀) ∙ cos(ωτ) ∙ dω = 1/π ∙ ∫ W(Ω) ∙ cos[(ω₀+Ω)τ]∙dΩ =

= 1/π ∙ [ ∫ W(Ω) ∙ cos(Ωτ)∙dΩ]∙ cos(ω₀τ) - 1/π ∙ [ ∫ W(Ω) ∙ sin(Ωτ)∙dΩ]∙ sin(ω₀τ); (1.4)

Учитывая, что ω₀ >> α:

В(τ) ≈ 1/π ∙ [ ∫ W(Ω) ∙ cos(Ωτ)∙dΩ]∙ cos(ω₀τ), (1.5)

В₀(τ) = 1/π ∙ ∫ W(Ω) ∙ cos(Ωτ)∙dΩ, (1.6)

где: W(Ω) – НЧ спектр мощности, равный спектру мощности W(ω), но смещенный в область низких частот на величину ω₀.

Использование свойства (1.3) дает возможность свести нахождение корреляционной функции полосового ВЧ процесса к определению функции корреляции соответствующего НЧ процесса.

Вычисление интегралов при нахождении функции корреляции необходимо

производить следующим образом:

- варианты 0; 1: интеграл берется интегрированием по частям (см. формулу в приложении к методуказаниям);

- вариант 2: несобственный интеграл берется по формуле (см. приложение к методуказаниям);

- вариант 3: несобственный интеграл берется по формуле (см. приложение к методуказаниям);

- вариант 4: интеграл вычисляется элементарно;

- вариант 5: интеграл вычисляется элементарно, с учетом соотношений (1.3) и (1.6), где W(Ω)= W₀;

- вариант 6: интеграл берется интегрированием по частям (см. формулу в приложении к методуказаниям), с учетом соотношений (1.3) и (1.6), где

W(Ω)= W₀∙ Ω/α;

- вариант 7: интеграл берется интегрированием по частям (см. формулу в приложении к методуказаниям), с учетом соотношений (1.3) и (1.6), где W(Ω)=W₀∙ [1-Ω/α];

- вариант 8: несобственный интеграл берется по формуле (см. приложение к методуказаниям), с учетом соотношений (1.3) и (1.6), где W(Ω)=W₀∙α²/(α ²+Ω²);

- вариант 9: несобственный интеграл берется по формуле (см. приложение к методуказаниям), с учетом соотношений (1.3) и (1.6), где W(Ω)=W₀∙exp[-Ω²/α²];

При расчете функции корреляции в варианте 4, ее следует привести к виду В₀(τ)=W₀∙α/π∙sin(α∙τ)/(α∙τ). Аналогично и для варианта 5. В данном виде легче строится график функции. Зная вид функции sin(α∙τ)/(α∙τ) и определив значения τ, при которых функция равна нулю: В₀(τ)=0 при sin(α∙τ)=0; α∙τ=kπ; τ= kπ/α, где k=1, 2,..., можно задавшись несколькими промежуточными значениями τ быстро рассчитать и построить график функции. К подобным видам приводятся функции корреляции в вариантах 0 и 1 при использовании формулы интегрирования по частям и формулы тригонометрического преобразования для (1-cosX) из приложения к методуказаниям.

При построении графика В(τ) при ω₀≠0, огибающую В₀(τ) следует строить с указанием масштаба по оси τ, а ВЧ заполнение с частотой ω₀ – показать условно.

Определение эффективной ширины энергетического спектра ∆ω_э и

интервала корреляции τ_к случайного процесса для разных вариантов задания можно по разному. Существует несколько способов их определения:

а). Определение ∆ω_э и τ_к методом эквивалентного прямоугольника. Этот метод обычно используется при неограниченно протяженных В₀(τ) и W(ω). В нем необходимо взять интегралы от W(ω) и В(τ) [4 с.163-164]:

 

∆ω_э = ∫W(ω)∙dω / W_макс.(ω), (1.7)

τ_к = ∫В₀(τ)∙dτ / В₀(0), (1.8)

где: W_макс.(ω) – максимальное значение энергетического спектра;

В₀(τ) – функция корреляции огибающей случайного процесса.

б). Если спектр процесса идеализирован, т. е. отличен от нуля в конечной полосе частот, то ∆ω_э можно принять равной полосе частот, в которой W(ω) ≠0. Этот метод можно применить для ограниченного по частоте энергетического спектра.

в). Можно вычислить τ_к по графику В₀(τ) как временной интервал от τ = 0, до τ = τ_к, при котором В₀(τ) ≈ 0,1∙В₀(0). Аналогично и для ∆ω_э – по графику W(ω) как полоса частот от ω = 0, до ω = ∆ω_э, при которой W(ω) ≈ 0,1∙W_макс.(ω). Этот метод также как и метод а) может быть применен для случая неограниченно протяженных В₀(τ) и W(ω).

г). Интервал корреляции τ_к можно найти как минимальное значение τ, при котором В₀(τ) = 0. Этот метод применим для случайных процессов, функция корреляции которых имеет «нулевые точки» (варианты 0, 1, 4, 5).

При взятии интегралов в методе а) чаще всего используются формулы для несобственных, табличных интегралов (см. приложение к методуказаниям), по которым можно провести необходимые расчеты.

Математическое выражение для функции плотности вероятности р(х) нормального случайного процесса можно найти в [2- с.46; 4- с.140]. Значение дисперсии случайного процесса σ² можно определить по корреляционной функции В(τ):

D(x) = σ² = В(τ=0) = В(0). (1.9)

Математическое выражение функции распределения F(x) и расчет вероятности попадания значений случайного процесса в заданный интервал

Ρ(c < x ≤ d) приводятся в [ 2- с.47, пример 2.6; 4- с.140-141]:

Ρ(c < x ≤ d) = F(d) – F(c) = Ф[(d-m)/σ] - Ф[(c-m)/σ], (1.10)

где: m – математическое ожидание (среднее значение) случайного процесса;

Ф(х) – интеграл вероятностей.

Ф(х) = 1/√2π∙∫exp(-t²/2)∙dt; (1.11)

Таблица значений интеграла вероятностей [13] и рекуррентная формула их расчета [1] приведены в приложении к методуказаниям. Обратите внимание на виды интеграла вероятностей, их взаимосвязь и определение значений одного интеграла через другой. Следует внимательно брать значения требуемого интеграла вероятностей из литературы, учитывая, что их обозначения в разной литературе разные и не имеют корреляции.

Задача 2

Стационарный случайный процесс Х(t) имеет одномерную функцию

плотности вероятности (ФПВ) мгновенных значений р(х), график и параметры

которой приведены в таблице 3.

Требуется:

1. Определить параметр h ФПВ.

2. Записать математическое выражение и построить график ФПВ- р(х).

3. Определить функцию распределения вероятностей (ФРВ) мгновенных

значений случайного процесса - F(x).

4. Записать математическое выражение и построить график ФРВ- F(х).

5. Рассчитать значения математического ожидания М(х) и дисперсии D(х).

Таблица 3

Последняя цифра номера варианта	ФПВ р(х)	Предпоследняя цифра номера варианта	Параметры ФПВ
			а	c	d	b	e
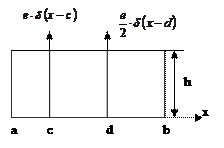0 или 9			-2	-1			0,1
					0,25
1 или 8			-1				0,2
	-2				0,3
2 или 7							0,25
	-3				0,28
h

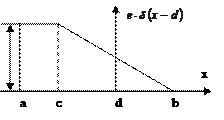
Или 6