Метод использования частотных преобразований

Данный метод заключается в последовательном прохождении следующих этапов:

 

1. Дискретизация импульсной характеристики входного сигнала.
2. Нахождение комплексного частотного коэффициента передачи сигнала (передаточной функции).
3. Формирование Z -преобразования от частотного коэффициента передачи.
4. Дискретное преобразование Фурье от импульсной характеристики.

Условно этот алгоритм можно представить в виде следующей записи:

 

,

 

где – дискретное преобразование Фурье от импульсной характеристики. В виде схемы этот алгоритм для сигнала представлен на рис. 3.2.7.5.

 

 

Рис. 2. Структура метода использования частотных преобразований.

 

На рис. 2 на данной схеме сначала происходит дискретное преобразование Фурье (ДПФ) от входного сигнала, суммированного с шумом . Получается спектральная плотность от входного сигнала по k .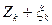

При их суммировании второй этап – спектр умножается на передаточную функцию .

Далее берется обратное преобразование Фурье, и получаем выходной дискретный сигнал. Таким образом, через частотное преобразование получили частотную передаточную функцию от сигнала .

На этом принципе основаны конвольверы – устройства преобразования сигнала в частотную передаточную функцию, и обратно, от частотной передаточной функции к исходному сигналу

 

Ход работы:

1. Поострить спектр отдельно взятой гармоники (кратной частоте F1):

 

 

 

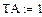
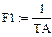
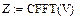
CFFT – быстрое преобразование Фурье

 

 

 

 

Рис. 3 Спектр гармоники кратной частоте F1

 

Из расчетов видно, что Z10 и Z90 отличаются только знаком мнимой части, т.е. они комплексно сопряженные.

 

1. Построить спектр гармоники (не кратной частоте F1):

 

 

 

 

 

 

 

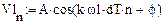
Рис. 4 Спектр гармоники не кратной частоте F1

 

Из графика видно, что изменение частоты на 0,5 Гц ведет к увеличению числа гармоник.

Амплитудный спектр одинаковый, симметричный и комплексно сопряженный.

 

1. БПФ от прямоугольного импульса:

 

 

 

 

 

Рис. 5 Прямоугольный импульс (дискретный)

 

 

 

 

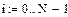
Рис. 6. Быстрое преобразование Фурье от прямоугольного импульса

 

 

1. БПФ от кривой Гаусса:

 

Рис. 6. Дискретный импульс Гаусса

 

Применим БПФ:

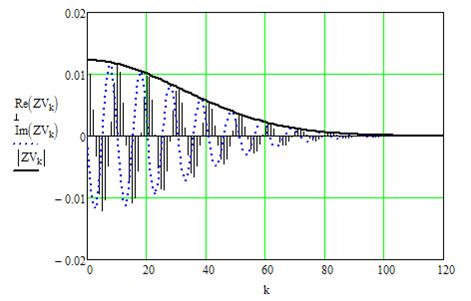
Рис. 7. Быстрое преобразование Фурье от импульса Гаусса

 

1. БПФ от символа Кронекера:

 

 

Рис. 8. Исходная функция

 

 

Рис. 9.1. Быстрое преобразование от символа Кронекера

 

 

Рис. 9.2. Быстрое преобразование от символа Кронекера

 

 

Выводы:

 

1. Построен спектр гармоники кратной частоте F1. Из расчетов видно, что Z10 и Z90 отличаются только знаком мнимой части, т.е. они комплексно сопряженные.

2. Построен спектр гармоники не кратной частоте F1. Из рис. 4 видно, что изменение частоты на 0,5 Гц ведет к увеличению числа гармоник. Амплитудный спектр одинаковый, симметричный и комплексно сопряженный.

3. Взято быстрое преобразование Фурье от прямоугольного импульса.

4. В системе математического моделирования MathCAD прямые преобразования Фурье осуществляются с помощью функций FFT(V), IFFT(V), где V – заданный вектор. Обратные преобразования Фурье вводятся функциями ICFFT(V), CFFT(V). Также можно использовать функции fft(V) и cfft(V) – те же самые алгоритмы, но с другими коэффициентами нормировки.

5. Взяты БПФ от символа Кронекера и Гауссовой кривой.