Лабораторная работа №4
по курсу «Основы радиоэлектроники и связи» на тему:
«Цифровые фильтры и их характеристики»
Преподаватель: профессор Трофимов А. Т.
Выполнил: студент 4 курса гр. № 4141
Понкин Д. О.
Дубна, 2011
СОДЕРЖАНИЕ
ЦЕЛЬ РАБОТЫ.. 3
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 3
2. ПРАКТИЧЕСКАЯ ЧАСТЬ. 4
2.1. Переходная и импульсная характеристики БИХ-фильтров 1-го и 2-го порядка. 4
2.2. Частотные характеристики БИХ-фильтров 1-го и 2-го порядка. 6
2.3. Реализация КИХ-фильтров 1-го и 2-го порядков. 7
ВЫВОДЫ.. 8
ЦЕЛЬ РАБОТЫ
Целью работы является закрепление знаний о принципах построения цифровых фильтров и их характеристиках.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В цифровых фильтрах входной и выходной сигналы являются дискретными последовательностями цифровых отсчетов сигналов.
Цифровая фильтрация заключается в цифровом преобразовании последовательности числовых отсчетов входного сигнала в последовательность числовых отсчетов выходного сигнала.
Импульсную характеристику цифрового фильтра можно трактовать как результат дискретизации согласно теореме отсчетов непрерывной импульсной характеристики соответствующего аналогового фильтра. В цифровых фильтрах импульсные характеристики могут иметь конечное (КИХ-фильтры) и бесконечное (БИХ-фильтры) число отсчетов. Выходная последовательность представляет собой дискретную свертку входного сигнала с импульсной характеристикой цифрового фильтра.
Системная функция является отношением z-преобразования выходного сигнала к z-преобразованию входного сигнала и связана с импульсной характеристикой, как

Данная функция играет для цифрового фильтра ту же роль, что и передаточная функция для аналогового фильтра.
Комплексный частотный коэффициент передачи фильтра  .
.
Он, как и спектр дискретного сигнала, имеет периодическую структуру с периодом по оси частот, равным частоте дискретизации. Это позволяет либо выделить, либо подавить отдельные составляющие спектра дискретного входного сигнала.
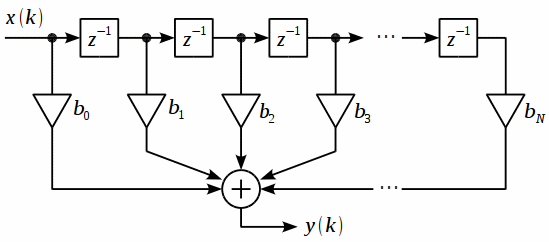
Рис. 1. Структурная схема КИХ-фильтра

Рис. 2. Структурная схема БИХ-фильтр
ПРАКТИЧЕСКАЯ ЧАСТЬ
Переходная и импульсная характеристики БИХ-фильтров 1-го и 2-го порядка
Запишем разностное уравнение БИХ-фильтра 1-го порядка и построим графики его переходной, импульсной характеристик. Переходная характеристика есть отклик цепи на функцию Хэвисайда (или единичного скачка):


Рис. 2.1. Переходная характеристика цифрового БИХ-фильтра 1-го порядка
Подадим на вход фильтра дельта-функцию. Отклик фильтра есть импульсная характеристика:

Рис. 2.2. Импульсная характеристика цифрового БИХ-фильтра 1-го порядка
Вывод: Переходная и импульсная характеристики цифрового БИХ-фильтра 1-го порядка соответствуют обычной интегрирующей RC-цепочке.
Запишем разностное уравнение БИХ-фильтра 2-го порядка и построим графики его переходной, импульсной характеристик. Переходная характеристика есть отклик цепи на функцию Хэвисайда (или единичного скачка):

Рис. 2.3. Переходная характеристика БИХ-фильтра 2-го порядка
Подадим на вход БИХ-фильтра 2-го порядка дельта-функцию. Отклик фильтра есть импульсная характеристика:

Рис. 2.4. Импульсная характеристика цифрового БИХ-фильтра 2-го порядка
Вывод: Переходная и импульсная характеристики цифрового БИХ-фильтра 2-го порядка такие же, как и у аналогового колебательного контура.






