При анализе непериодических (импульсных) сигналов их формально заменяют периодическими сигналами с бесконечно большим интервалом (периодом) следования 
.
Положим, что некоторая заданная функция 
аналитически описывает одиночный импульсный (иногда называют финитным) сигнал конечной длительности (рисунок 1.5, а). Мысленно дополнив его такими же импульсными сигналами, следующими с некоторым интервалом 
(рисунок 1.5, б), получим периодическую последовательность аналогичных импульсов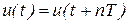 
.
 |
а)
б)
Рисунок 1.5 − Непериодические сигналы:
а) − один импульс; б) − условное периодическое представление
Для того чтобы вне искусственно введенного интервала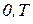 
исходный сигнал был равен нулю, необходимо увеличить период повторения импульсов. При увеличении периода и все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность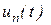 
вновь станет одиночным импульсом .
Периодическая функция для этого случая запишется так
. (1.14)
Так как период следования 
, то
. (1.15)
В предельном случае, когда период , равные расстояния между спектральными линиями уменьшаться настолько, что спектр станет сплошным, а амплитуды отдельных спектральных составляющих окажутся бесконечно малыми. При этом частота следования импульсов 
и превращается в 
, дискретная переменная 
− в мгновенную (текущую) частоту 
, а сумма трансформируется в интеграл. Периодическая последовательность импульсов 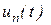станет одиночным импульсом и выражение (1.15) запишется в виде
. (1.16)
Здесь интеграл в скобках является комплексной функцией частоты. Обозначив его
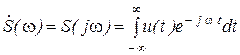, (1.17)
получим
. (1.18)
Соотношения (1.17) и (1.18) называют соответственно прямым и обратным преобразованиями Фурье. Они связывают между собой вещественную функцию времени (сигнал) и комплексную функцию частоты 
.
Таким образом, интеграл Фурье (1.17) содержит непрерывную (сплошную) последовательность спектральных составляющих сигнала с бесконечно малыми амплитудами. Функцию называют спектральной плотностью. Она характеризует интенсивность сплошного распределения амплитуд гармоник непериодического сигнала вдоль оси частот . В этом основное отличие спектральной плотности непериодического сигнала от дискретного спектра периодического сигнала, в котором каждая гармоническая составляющая имеет вполне определенное значение частоты и отстоит от соседней на величину 
. Дискретный спектр имеет размерность амплитуды (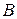
или 
). Спектральная плотность имеет размерность 
или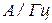 
.
Определим спектральную плотность прямоугольного импульса. Пусть имеется прямоугольный импульс с амплитудой 
и длительностью 
(рисунок 1.6, а). Так как анализируемый сигнал расположен на временном интервале 
, то, в соответствии с (1.17), получим
(1.19)
На рисунке 1.6, б) показан модуль спектральной плотности прямоугольного импульса напряжения.
а) б)
Рисунок 1.6 − Прямоугольный импульс:
а) − временная диаграмма; б) − спектральная плотность
Сравнив выражения для спектральной плотности одиночного прямоугольного импульса (1.19) и спектра периодической последовательности таких же импульсов (1.9) можно сделать заключение, что модуль спектральной плотности и огибающая гармоник дискретного спектра совпадают по форме и отличаются лишь масштабом по оси амплитуд.
