Составляющие
При разложении периодического колебания 
в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут
(1.2)
или
(1.3)
Интервал ортогональности в обоих случаях совпадает с периодом 
функции .
Система функций (1.2) приводит к тригонометрической форме ряда Фурье, а система (1.3) − к комплексной форме. Между этими двумя формами существует простая связь.
Представим периодический сигнал наиболее распространенной тригонометрической формой ряда Фурье:
(1.4)
где:
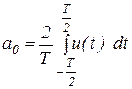− постоянная составляющая;
− амплитуда косинусоидальных составляющих;
− амплитуда синусоидальных составляющих.
Спектральную составляющую с частотой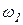 
называют первой (основной) гармоникой, а составляющие с частотами 
(
) −высшими гармониками периодического сигнала.
С математической точки зрения часто удобно выражение (1.4) описывающее данный сигнал, представлять в другой, эквивалентной форме ряда Фурье:
, (1.5)
где 
, 
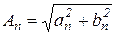− амплитуда, а 
− начальная фаза 
гармоники сигнала. Если перед 
стоит знак «+», тогда начальная фаза имеет знак «−».
В радиоэлектронике широко используется комплексный ряд Фурье
, (1.6)
где 
. (1.7)
Спектр периодического сигнала принято называть линейчатым или дискретным, так как он состоит из отдельных линий, высота которых равна амплитуде 
соответствующих гармоник. На рисунке 1.2 приведены спектры периодического сигнала: а) − амплитудный; б) − фазовый; в) – комплексный.
 |
а) б) в)
Рисунок 1.2 – Спектры периодических сигналов:
а) − амплитудный; б) − фазовый; в) – комплексный
Спектральный состав последовательности прямоугольных
Импульсов при различных периодах и скважности
В радиоэлектронике часто применяются прямоугольные периодические импульсы напряжения. На рисунке 1.3 показан отрезок последовательности прямоугольных импульсов длительностью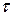 
с периодом следования 
. длительность импульсов 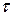может измеряться микросекундами или долями микросекунд. Что касается периода следования импульсов , то он может в сотни и тысячи раз превышать длительность импульсов. Отношение 
называется скважностью.
Для периодической последовательности прямоугольных импульсов напряжения комплексные амплитуды гармоник
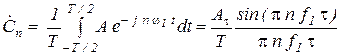, (1.8)
где 
.
Следовательно,
. (1.9)
Амплитудный спектр такой последовательности показан на рисунке 1.4. В частном случае при 
, поэтому
. (1.10)
Это колебание состоит из постоянной составляющей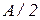 
и прямоугольной волны с амплитудой .
 |
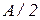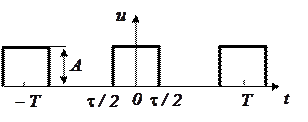Рисунок 
1.3 − Периодические прямоугольные импульсы
Рисунок 1.4 − Спектр периодических прямоугольных импульсов
