The system looses energy by a drag force
F D = – r×u,
or a voltage drope on the active resistor
uR= R×i,
therefore the amplitude has exponential decay on time
A (t) =А 0 × е - b ×t.
The equation of damped oscillations has a mode
, (3)
where x(t) – physical quantity, which oscillates; А 0 – initial amplitude of oscillations; b – damping coefficient; j0 – initial phase (phase constant).
Cyclic frequency of damped oscillations (is written with no index) less then eigenfrequency:
. (4)
Parameters of linear damping oscillations:
1) Relaxation of vibrations – lessening of amplitude in е =2,71 times. The time of relaxation:
t = 1 / b. (5)
2) As far as amplitude of damped oscillations uninterruptedly decreases A (t) =А0× е - b× t, then the value of oscillating quantity x(t) will never repeat. That’s why, the quantity
(6)
is called conventional period – minimal time, during which the value of oscillating quantity x(t) will be equal peak magnitude (amplitude).
3) Decay decrement is a relation of two neibouring amplitude:
D = At / At+T = e – b T. (7)
4) Logarithmic decay decrement (damping constant):
d = ln D =b T CONV, (8)
5) Quality factor of system
Q = w0 / 2b. (9)
In equation of oscillations (2) it is described both mechanical, and electromagnetic oscillations, therefore it is possible to set up correspondence of mechanical and electrical oscillations’ parameters:
| Mechanic oscillations | Electromagnetic oscillations |
| x(t)= x (t) – displacement from the equilibrium position of material point of oscillating device; | x(t)= q (t) – charge of oscillating circuit capacitor; |
| Parameters of a system: | |
| k – spring constant (stiffness of spring). m – mass of oscillating device. r – drag coefficient. | С – electrocapacity of the capacitor. L – inductance of the inductance coil. R – resistance of circuit. |
| Damping coefficient: | |
 ;
|  ;
|
| Cyclic frequency of damped oscillations: | |
 ;
|  ;
|
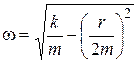| Quality factor of system: | |
 .
|  .
|
EXAMPLE OF PROBLEM SOLUTION
Example 2. The oscillating RLC- circuit consists of capacitor, and coil of inductance of 2 mH and resistor. At the initial moment of time charge on the capacitor plates is maximal and equals q 0= Q 0=2m C. Conventional period of oscillations 1 ms, logarithmic decay decrement is 0,8.
1) To write down the equation of oscillations of charge with numerical coefficients.
2) To define the capacity of capacitor and the resistance of resistor.
| Input data: L = 2 mH =0,002 H; Q 0= 2 m C =2·10–6 C; Т CONV = 1 s =10–3 s; δ= 0,8. | 
|
| Find: q (t), С, R –? |
Solution:
1) Oscillations in circuit will be damping. Let’s write the equation of damped oscillations of charge in a general view:
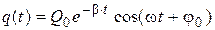, (2.1)
where Q 0 – the initial amplitude of charge, β – damping coefficient; ω – cyclic frequency of damped oscillations; j0 – initial phase.
From a definition of the conventional period T CONV = 2p / w we express cyclic frequency of damped oscillations:
w = 2p / T CONV. (2.2)
From a definition of initial value of oscillating quantity q 0= Q ×cos(j0) and considering that the oscillations beginning from the position of maximal charge on the capacitor Q, we find the initial phase of oscillations:
j0= arc cos(q 0 / Q)= arc cos(1)=0. (2.3)
From a definition of the logarithmic decay decrement is d=b T CONV, whence the coefficient of damping
b=d / T CONV. (2.4)
Let’s check, whether the right part of the formula (2.2) gives the unit of cyclic frequency [ rad/s ], and the left part of the formula (2.4) – measurement unit of damping coefficient [1 /s ]:
[w]= rad / s;
[b]= 1 / s.
Let’s substitute the numerical values in the formulas (2.2) and (2.4)
;
.
Let’ write down the equation of oscillation of charge with numerical coefficients
. (2.5)
2) Let’s substitute the equation of eigenfrequency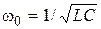 
into the definition of cyclic frequency of damped oscillations :
Þ 
(2.6)
and find expression of capacity of capacitor:
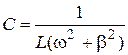. (2.7)
From a definition of the damping coefficient b= R/ 2 L we obtain resistance of resistor R:
R = 2β L. (2.8)
Let’s check, whether the right part of the formula (2.7) gives the unit of electrocapacity [ F ], and the left part of formula (2.8) – the unit of resistance [ Ω ]:
;
.
Let’s make the calculations:
; R = 2 · 300 · 2 · 10-3= 3,2 W.
Results: 1) 
,
2) C= 1,25×10-5 F , R = 3,2 Ω.
