Simple harmonic oscillations. The equation which describes the eigenmode of oscillations has the simple harmonic form:
, (1)
wherex(t) – physical quantity, which makes the oscillations; А – oscillation amplitude;j0 – initial phase (phase constant).
The time parameters of oscillations’ eigenmode are called eigen-parameters (or natural parameters) and are written down with index «0»:
Cyclic eigenfrequency of oscillations (changing of oscillations’ phase per one second):
w0 = 2p / Т 0 = 2p × n0, (2)
n0 – eigenfrequency of oscillations (number of oscillations per one second);
Т0 – eigenperiod of oscillations (minimal time interval of repeating of the value of oscillating quantity).
In equation of oscillations (1) it is described both mechanical, and electromagnetic oscillations, therefore it is possible to set up correspondence of mechanical and electrical oscillations’ parameters:
| Mechanic oscillations | Electromagnetic oscillations |
| x(t)= x (t) – displacement from the equilibrium position of material point of oscillating device; | x(t)= q (t) – charge of oscillating circuit capacitor; |
The velocity of material point of oscillating device:
 ;
| Current flowing through the inductance coil of the oscillating circuit:
 ;
|
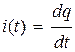Restoring force, acting on material point of oscillating device:
 ,
m – mass of oscillating device.
| Back EMF (self-induction) in the inductance coil of the oscillating circuit:
 ,
L – inductance of the inductance coil.
|
Cyclic eigenfrequency of spring pendulum oscillations:
 ,
k – spring constant (stiffness of spring).
| Cyclic eigenfrequency of oscillations in the oscillating circuit:
 ,
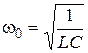С – electrocapacity of the capacitor.
|
Potential energy of elastic deformation:
 .
| Energy of capacitor electric field:
 .
|
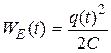Kinetic energy of oscillating device:
 .
| Energy of magnetic field of inductance coil:
 .
|
Total energy of oscillations is independence of time:
 ,
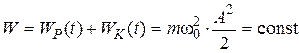А – amplitude of material point strain of oscillating device.
| Total energy of oscillations is independence of time:
 ,
Q – amplitude of capacitor charge of oscillating circuit.
|
Electromagnetic simple harmonic oscillations.
There are three main parameters, which are changing during oscillations in oscillating LC-circuit: q (t) – charge of capacitor, uC (t) – voltage on capacitor, i (t) – current flawing through coil. They have identical eigenfrequency, but amplitudes and initial phases are different. Relation between these quantities represented in two definition:
current: 
and electrocapacity 
.
Mathematic rules:
Differentiation rule of harmonic function:
1. The multiplication constant (amplitude) is necessary to take out of the derivative sign.
2. Derivative of harmonic function has phase lead relative to own function on p / 2:
and 
.
3. The result of derivation of harmonic function is necessary to multiply on derivative of a phase on time (on w0) (see example).
Integration rule of harmonic function:
1. The multiplication constant (amplitude) is necessary to take out of the integral sign.
2. Integral from harmonic function has phase lag from own function on p / 2:
and 
.
3. The result of integration of harmonic function is necessary to divide on derivative of a phase on time (on w0) (see example).
EXAMPLE OF PROBLEM SOLUTION
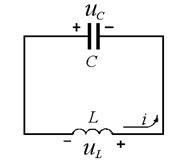
Example 1. The oscillation circuit consists of coil by inductance of L = 25 mH and capacitor. Current in circuit changes by the law i(t) = Im ×cosω0 t, where Im= 20 mА and ω0 = 104 rad/ s. 1) To get the equation of changing during the time charge of capacitor and voltage on the capacitor and on the coil. 2) To define total energy of oscillations in circuit.
| Input data: Im= 20 mА =0,02 А; ω0 = 104 rad/ s; L = 25 mH = 0, 025 H; I (t) = Im × cos(ω0 t). |
|
| Find: q (t), uC (t), eBACK(t), W –? |
Solution:
1) From definition of the current
we find expression of charge from current (as the integration – is the mathematical function, inverse to differentiation):
.
Let’s substitute the input equation of current oscillations in this expression and integrate. We get the equation of oscillations of charge of capacitor:
 ,
| (1.1) |
with amplitude  .
|
where Im – current oscillation amplitude; w0 – cyclic eigenfrequency of oscillations.
In (1.1) we consider that integral from harmonic function has phase lag from own function on p / 2.
From definition of the electrocapacity
we find the expression of dependence of the voltage on capacitor from charge of its plate:
.
Let’s substitute the equation (1.1) in this expression we get the equation of oscillations of voltage on capacitor:
 ,
| (1.2) |
with amplitude  .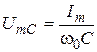
|
Electrocapacity can be found with the formula of oscillations’ cyclic eigenfrequency in the oscillating circuit:
, whence
, (1.3)
where L – circuit inductance. Substituted in the formula (1.2) the perceived equation for С (1.3) finally we obtain:
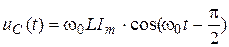. (1.4)
From the 2nd Kirchoff’s rule voltage on the inductance coil equal to Back EMF:
.
Let’s substitute the input equation of current oscillations in this expression and differentiate. We get the equation of oscillations of volktage on coil:
 ,
| (1.5) |
with amplitude  .
|
In (1.5) we consider that derivative of harmonic function has phase lead relative to own function on p / 2.
2. Total energy of oscillations in circuit equals the sum of energy of electric field in capacitor W E and energy of magnetic field in coil W М:
W = W E + W М;
.
Substituting the expression for С from the formula (1.3), amplitude of oscillations of voltage on capacitor (1.2) and input equation of current oscillations, we get
. (1.6)
Let's note, a total energy of oscillations has no time dependence, because absence of power loss.
Let’s check, whether the right part of equation of amplitude (1.1) gives the unit of charge [ C ], of equation of amplitude (1.4) the unit of voltage [ V ] and the formulas of amplitude (5) the unit of energy [ J ].
; 
;
.
Substituted numerical values, let’s write down the equation of changing q and uC with numerical coefficients and calculate the full energy of oscillations in circuit
; 
;
; 
.
Results: 
, 
,
, 
.
