Для операции сложения и умножения в кольце справедливы все следствия, полученные из законов ассоциативности и коммутативности в предыдущем параграфе. В частности, можно определить сумму и произведение любого конечного числа элементов, для которых верны правила оперирования, аналогичные и которые не зависят от порядка данных элементов.
Свойства I - III показывают, что кольцо относительно операции сложения является коммутативной группой. Поэтому во всяком кольце существует элемент 0, называемый нулем кольца, со свойством
для любого a. Далее, для любого a существует противоположный элемент -a такой, что
Из законов сложения I - III следует (как для всякой коммутативной группы) существование в любом кольце операции вычитания, обратной сложению. Умножение может и не обладать обратной операцией, как, например, в кольце целых чисел или в кольце многочленов.
Следствие закона дистрибутивности. Прежде всего из VI и IV следует, очевидно, вторая форма закона дистрибутивности:
Далее, обе формы закона дистрибутивности оказываются верными также и для разности, т. е.
Для доказательства первого равенства надо проверить, что элемент (a - b)c удовлетворяет определению разности элементов ac и bc. Но действительно
Второе равенство доказывается аналогично.
Теорема 1. Если один из сомножителей равен нулю, то и все произведение равно нулю, т. е.
, для любого a.
Докажем лишь первое из равенств, так как второе вытекает из первого при помощи IV. По определению нуля и разности 0 = b - b для любого b. Отсюда 
Однако теорема, обратная теореме 1, верная для чисел, уже не сохраняется для любых колец, иными словами, если произведение двух элементов кольца равно нулю, то нельзя утверждать, что хотя бы один из них равен нулю. Так, в приведенном выше примере 10 кольца, составленного из пар (a, b) целых чисел, нулем является, очевидно, пара (0, 0). Если взять целые числа и, то пары (a, 0) и (0, b) отличны от нуля кольца, но (a, 0)(0, b) = (0, 0).
Определение 1. Элементы 
кольца, для которых, но 
называются делителями нуля. Кольцо без делителей нуля называется также областью целостности.
Теорема 2. Из 
следует 
, если только 
и не является делителем нуля.
Теорема 3. (Свойства разности) В любом кольце разность элементов обладает следующими свойствами:
а) 
тогда и только тогда, когда 
;
б) 
в) 
г) 
Подмножество M кольца R называется подкольцом, если оно само является кольцом при тех эе операциях сложения и умножения, которые определены в кольце R.
Так, кольцо четных чисел является подкольцом кольца целых чисел, а последнее в свою очередь - подкольцом кольца рациональных чисел.
При выяснении того, является ли данное множество кольца подкольцом, нет надобности проверять справедливость всех свойств кольца. Большинство из них автоматически переходит с кольца на любое его подмножество. Удобнее всего пользоваться для этого такой теоремой:
Теорема 4. Для того чтобы непустое подмножество M кольца R было его подкольцом, необходимо и достаточно, чтобы сумма, разность и произведение любых двух элементов из M снова принадлежали M.
Все теоремы из раздела Кольца, выведенные для колец, остаются верными, в частности, для полей.
Как всякое кольцо, поле является группой относительно операции сложения. Все элементы поля, не равные нулю, образуют группу относительно операции умножения. Группа по сложению всех элементов поля называется аддитивной, а группа по умножению всех его элементов, отличных от нуля, - мультипликативной группой поля. Поле вполне определяется заданием двух этих групп, заданием произведений нуля на все элементы и требованием дистрибутивного закона для любых его элементов, включая нуль. Отсюда уже следует, что произведение любого элемента на нуль равно нулю.
Из свойств мультипликативной группы следует, что в поле существует единица, т. е. такой элемент e, что 
для любого 
.
Теорема 5. Поле не имеет делителя нуля, т. е. если ab = 0, то либо a = 0, либо b = 0.
Теорема 6. Всякое конечное кольцо без делителей нуля, содержащее более одного элемента, является полем.
Теорема 7. (Свойства частного)
а) Если 
, то 
, тогда и только тогда, когда 
б) Если , то 
;
в) Если , то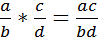 
;
г) Если 
, то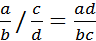 
.
Существуют поля, содержащие элементы a ≠ 0 такие, что na = 0 при целом n, отличном от нуля. Так, в поле из двух элементов 0 и e имеем: 2e = e + e = 0. Справедливо утверждение:
Теорема 8. Для любого поля P имеет место один из двух случаев:
а) для любого элемента a ≠ 0 и любого целого числа n ≠ 0 кратное na также отлично от нуля;
б) существует единственное простое число p такое, что pa = 0 для любого элемента a. (Под простым числом понимается натуральное число, отличное от 1 и не делящееся ни на какое натуральное число, кроме 1 и самого себя)
Характеристикой поля P называется число 0, если na ≠ 0 для любого элемента a ≠ 0 и любого целого числа n ≠ 0 и простое число p такое, что pa = 0 для любого элемента a в противном случае. Так как для числа 1 и любого целого n будет n · 1 = n, то все числовые поля имеют характеристику 0.
Конечное поле
Конечное поле или поле Галуа — поле, состоящее из конечного числа элементов. Конечное поле обычно обозначается 
или GF(q), где q — число элементов поля.
Свойства:
- Характеристика конечного поля является простым числом;
- Число элементов любого конечного поля есть его характеристика в натуральной степени: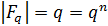 
;
- Для каждого простого числа p и натурального n существует конечное поле из 
элементов, единственное с точностью до изоморфизма. Это поле изоморфно полю разложения многочлена 
;
- Мультипликативная группа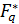 
конечного поля 
является циклической группой порядка 
;
o В частности, в конечном поле всегда существует примитивный элемент 
, порядок которого равен , то есть 
и 
для 
;
o Любой ненулевой элемент 
является некоторой степенью примитивного элемента: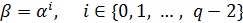 
;
- Поле 
содержит в себе в качестве подполя 
тогда и только тогда, когда 
является делителем 
.
Построение поля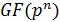 
, где p — простое число, n — натуральное число, начинается с построения его простого подполя (которое совпадает со всем полем при n =1).
- Простое поле 
строится как кольцо 
вычетов по модулю p, которое в виду простоты не имеет делителей нуля и является полем.
Элементы — числа 
. Операции проводятся как с обычными целыми числами с приведением результата по модулю p;
- Поле 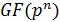при n>1 строится как факторкольцо 
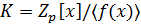, где 
— неприводимый многочлен степени n над полем . Таким образом, для построения поля из 
элементов достаточно отыскать многочлен степени n, неприводимый над полем ;
- Элементами поля K являются все многочлены степени меньшей n с коэффициентами из . Арифметические операции (сложение и умножение) проводятся по модулю многочлена , то есть, результат соответствующей операции — это остаток от деления на с приведением коэффициентов по модулю p.
Для алгоримта AES (Rijndael) были разработаны собственные неприводимые полиномы в поле 
, а также операции сложения и умножения, рассмотренные в следующих разделах.
