Непустое множество R называется кольцом, если в нем определены две алгебраические операции: сложение, ставящее в соответствие каждым двум элементам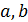 
элемент 
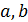, называемый их суммой, и умножение, ставящее в соответствие каждым двум элементам элемент 
, называемый их произведением, причем эти операции обладают следующими свойствами:
I. (Коммутативность сложения) a + b = b + a;
II. (Ассоциативность сложения) a + (b + c) = (a + b) + c;
III. (Обратимость сложения) Для любых a и b из R уравнение a + x = b имеет (по крайней мере, одно) решение, т. е. существует элемент такой, что a + c = b;
IV. (Коммутативность умножения) ab = ba;
Термин "кольцо" применяется также к множествам с некоммутативным или даже неассоциативным умножением. Формулировки других свойств также меняются.
V. (Ассоциативность умножения) a(bc) = (ab)c;
VI. (Дистрибутивность умножения относительно сложения)
(a + b)c = ac + bc.
При обычных операциях сложения и умножения кольцом является:
1. Множество целых чисел.
2. Множество рациональных чисел.
3. Множество действительных чисел.
4. Множество рациональных чисел.
5. Множество, состоящее лишь из одного числа 0.
6. Множество четных чисел и вообще множество целых чисел, кратных некоторому числу n.
7. Множество комплексных чисел 
с целыми 
и 
(так называемое кольцо целых комплексных чисел).
8. Множество действительных чисел 
, где a и b – целые числа.
Множество натуральных чисел, а также множество всех положительных рациональных чисел кольцами не являются, так как не выполняется аксиома III.
9. Большую роль в алгебре играет кольцо многочленов с одним или несколькими неизвестными и коэффициентами из некоторого кольца R. При этом за операции сложения и умножения принимаются обычные действия над многочленами, известные из школьной алгебры. Эти действия имеют смысл, так как они сводятся к сложению и умножению коэффициентов многочленов, а последние принадлежат к кольцу R, где указанные действия определены
10. Пары (a, b) целых чисел образуют кольцо, если операции определены по формулам:
.
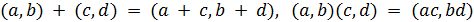Примеры колец показывают, что в отношении обратной операции для умножения (в отличие от сложения) различные кольца обладают совершенно различными свойствами. Так, в кольце целых чисел деление выполняется лишь в исключительных случаях, причем все элементы кольца делятся на +1 и –1. В кольце же рациональных чисел деление всегда возможно (кроме деления на 0). Желая изучить свойства обратной операции для умножения, приходим к важнейшему частному случаю кольца - полю.
Полем называется кольцо P, обладающее следующими свойствами:
VII. (Обратимость умножения) Для любых 
, где 
, уравнение 
имеет (по крайней мере одно) решение, т. е. существует элемент 
такой, что 
.
VIII. 
содержит по крайней мере один элемент, отличный от нуля.
Из примеров 1-10 колец только 2, 3 и 4, т. е. рациональные, действительные и комплексные числа, являются полями. В примере 5 свойство VII выполнено, так как вообще нет элемента a ≠ 0, но не выполнено свойство VIII. В остальных примерах не выполняется свойство VII.
