Расчет первичных параметров передачисимметричного кабеля

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение

высшего профессионального образования

«Юго-западный государственный университет»

Кафедра Телекоммуникаций

Расчет первичных и вторичных параметров симметричной кабельной цепи звездной скрутки

Вариант 27

Выполнил: студент группы СК-81

Волынец Ю.А.

Проверил: Демьяненко Ю.В.

Курск 2011

Расчет первичных параметров передачисимметричного кабеля

Рисунок 1 – Диаметр изолированной жилы

Рисунок 2 – Диаметр элементарной группы кабеля

1.1 Активное сопротивление

R₀ ‒ сопротивление цепи по постоянному току,(Ом/км)

F(x) ‒ функция, учитывающая действие поверхностного эффекта

p ‒ коэффициент, учитывающий потери на вихревые токи в жилах второй цепи элементарной группы, для звездной скрутки р =5

G(x) ‒ функция, учитывающая действие эффекта близости

d₀‒ диаметр жил, мм

а ‒ расстояние между центрами жил, мм

H(x) ‒ функция учитывающая действие эффекта близости.

Формула для расчета сопротивления цепи по постоянному току имеет вид:

ρ = 1/σ – удельное сопротивление материала жил, для алюминия 0,028 Ом·мм²/м;

χ – коэффициент укрутки, равен 1,02.

Диаметр изолированной жилы:

d _к – диаметр корделя, равный 0,8 мм

Δ = n∙t _л – общая толщина лент, наложенных поверх корделя, 0,12 мм.

Расстояние между центрами жил:

Коэффициент вихревых токов:

μ_а=μ₀·μ – абсолютная магнитная проницаемость, μ₀ = 4π·10^-7, Гн/м,

μ – относительная магнитная проницаемость равна 1

σ – удельная проводимость материала проводников 37x10⁶

Расчетные частоты в зависимости от заданного диапазона

Заданный диапазон, кГц f_н... f_в	f ₁	f ₂	f ₃	f ₄
12-252

k(12кГц)=1871,4 1/м

k(40кГц)=3416,6 1/м

k(120кГц)=5917,8 1/м

k(252кГц)=8575,8 1/м

Определение параметров x, F(x), G(x), H(x)

x₁₂=1,2

x₄₀=2,2

x₁₂₀=3,8

x₂₅₂=5,6

f, кГц
x	1,2	2,2	3,8	5,6
F(x)	0,0134	0,117	0,604	1,252
G(x)	0,037	0,221	0,55	0,861
H(x)	0,061	0,207	0,446	0,55
Q(x)	0,993	0,942	0,718	0,509

44,324 Ом/км

Составляющая активного сопротивления Rм, обусловленная потерями в окружающих металлических массах (соседних группах и металлической оболочке), на частоте 200 кГц определяется из таблицы как сумма потерь в смежных четверках и оболочке.

Расчет потерь в металле для другой частоты производиться по формуле:

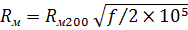
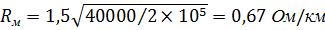
1.2 Расчет индуктивности

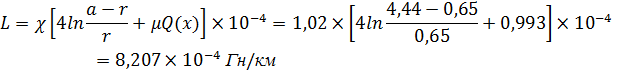
1.3 Расчет емкости

где ε_экв – эквивалентная относительная диэлектрическая проницаемость изоляции жил, для кордельно-бумажной – 1,3

ψ – коэффициент, учитывающий близость соседних проводников и металлической оболочки.

Поправочный коэффициент ψ, характеризующий близость проводов цепи к заземленной оболочке и другим проводникам, при звездной скрутке определяется по формуле:

Где d3 – диаметр элементарной группы, скрученной в звездную четверку, определяется из выражения:

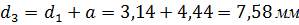
1.4 Проводимость изоляции

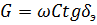
где 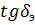– тангенс угла диэлектрических потерь комбинированной изоляции

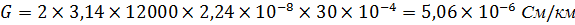
2 Расчет вторичных параметров

К вторичным параметрам относятся:

α ‒ коэффициент затухания;

β ‒ коэффициент фазы;

Z_в – волновое сопротивление;

t – время распространения;

U – скорость распространения;

2.1 Коэффициент затухания:

где ‒составляющая затухания за счет потерь в металле;

‒ составляющая затухания за счет потерь в диэлектрике.

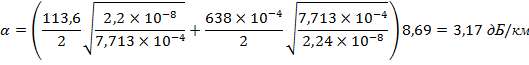
2.2 Коэффициент фазы:

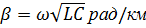
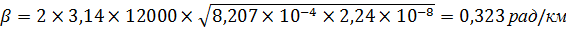
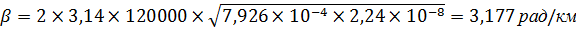
2.3 Волновое сопротивление:

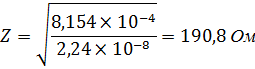
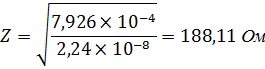
2.4 Расчет скорости распространения

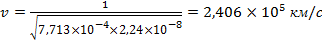
F, кГц

R, Ом/км 44,324 52,25 79,9 113,6

L, Гн/км 8,207×10^-4 8,154×10^-4 7,926×10^-4 7,713×10^-4

G, См/км 5,06×10^-6 3,2×10^-5 2,11×10^-4 6,38×10^-4

α, дБ/км 1,01×10^-4 1,22×10^-4 2,02×10^-4 3,17×10^-4

β, рад/км 0,323 1,074 3,177 6,581

Z, Ом 191,4 190,8 188,11 185,6

v, км/с 2,334×10⁵ 2,34×10⁵ 2,373×10⁵ 2,406×10⁵

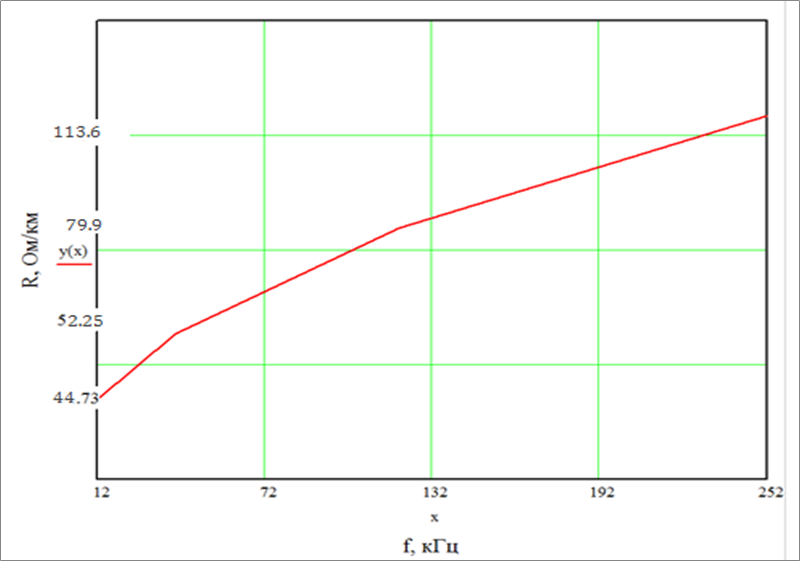
Рисунок 3 – Зависимость активного сопротивления от частоты

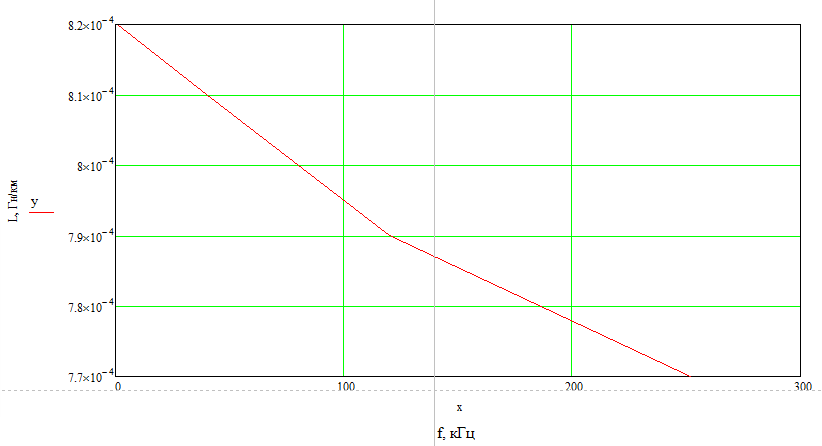
Рисунок 4 – Зависимость индуктивности от частоты

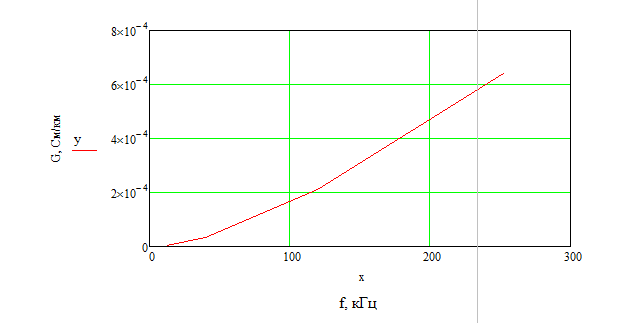
Рисунок 5 – зависимость проводимости от частоты

Рисунок 6 – зависимость коэффициента затухания от частоты

Рисунок 7 – Зависимость коэффициента фазы от частоты

Рисунок 8 – Зависимость волнового сопротивления от частоты

Рисунок 9 – зависимость скорости распространения от частоты