 ,
,  ,
,  ,
,  - отклонения от предшествующих установившихся значений
- отклонения от предшествующих установившихся значений
Требуется:
1. Построить область устойчивости и выбрать допустимые значения параметров регулятора: коэффициента усиления 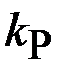 и постоянной времени
и постоянной времени 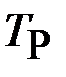 .
.
2. Проверить устойчивость по критерию Гурвица.
3. Подготовиться к ответу на контрольные вопросы.
Контрольные вопросы:
1. Понятие передаточной функции звена (см. здесь и далее в дисциплине «Теория автоматического управления»).
2. Правило определения передаточной функции замкнутой системы автоматического регулирования (САР) по передаточным функциям звеньев. Как получается структурная схема САР с единичной обратной связью из исходной?
3. Понятие характеристического уравнения, его связь с передаточной функцией.
4. Правило построения границы D -разбиения. Что можно сказать о корнях характеристического уравнения замкнутой системы, параметры которой находятся на границе D -разбиения? Как получают претендента на область устойчивости?
5. Как проверить, является ли “претендент” областью устойчивости?
6. Понятие о критическом коэффициенте усиления “разомкнутой” системы. Размерность коэффициента усиления “разомкнутой” системы.
7. Конструкция и схема обмоток синхронного генератора. Типы возбудителей и способы управления ими (см. в дисциплине «Электрические машины»).
1.3. Пример применения метода D -разбиения для определения области допустимых значений параметров регулятора  и
и 
Заданы:
- структурная схема системы АРВ (рис. 1.1);
- параметры звеньев генератора и возбудителя: 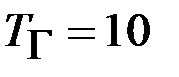 с;
с;  с;
с;
 ;
;  .
.
Решение
Передаточная функция исследуемой замкнутой системы:
 ,
,
следовательно, характеристическое уравнение этой системы имеет вид
 .
.
После подстановки выражений передаточных функций звеньев, характеристическое уравнение принимает вид:
 .
.
После замены  на
на  и подстановки принятых исходных данных находим
и подстановки принятых исходных данных находим
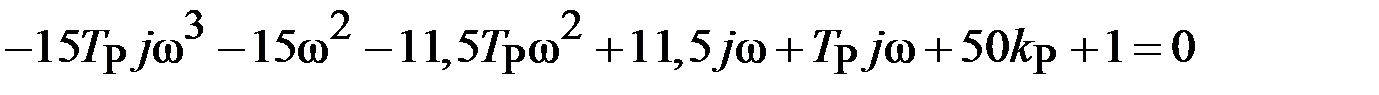 .
.
Приравнивая нулю порознь действительную и мнимую части, получаем систему уравнений, определяющих границу устойчивости:

главный определитель которой
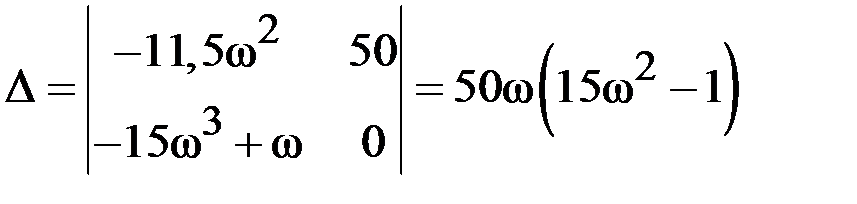 .
.
Решение этой системы относительно параметров  и
и  имеет вид
имеет вид
 (1.1)
(1.1)
Кривая D -разбиения плоскости двух параметров имеет совпадающие точки, соответствующие  и
и  , так как
, так как 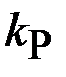 и
и  являются чётными функциями частоты. Поэтому её построение достаточно выполнить только для положительных частот, для отрицательных частот кривая D -разбиения будет повторяться. Задаваясь значениями
являются чётными функциями частоты. Поэтому её построение достаточно выполнить только для положительных частот, для отрицательных частот кривая D -разбиения будет повторяться. Задаваясь значениями  от 0 до
от 0 до  , по выражениям (1.1) рассчитываем значения
, по выражениям (1.1) рассчитываем значения  и
и  и строим кривую D -разбиения (рис. 1.2, а). Заметим, что главный определитель
и строим кривую D -разбиения (рис. 1.2, а). Заметим, что главный определитель  обращается в нуль не только при
обращается в нуль не только при  , но и при
, но и при  . Параметры
. Параметры  и
и  принимают при этом значения
принимают при этом значения  и
и  и
и  . При
. При 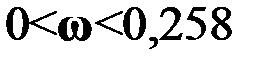 значение главного определителя
значение главного определителя  (кривая D -разбиения расположена в четвёртом квадранте), а при
(кривая D -разбиения расположена в четвёртом квадранте), а при  значение
значение  (кривая D -разбиения расположена в первом квадранте).
(кривая D -разбиения расположена в первом квадранте).
Штриховка кривой D -разбиения осуществляется согласно правилу: при изменении  от
от  до
до  кривая D -разбиения штрихуется слева, если
кривая D -разбиения штрихуется слева, если  , и справа, если
, и справа, если  . Так при изменении знака
. Так при изменении знака  главный определитель
главный определитель  также меняет знак, то при двукратном обходе кривой D -разбиения она оказывается два раза заштрихованной с одной стороны.
также меняет знак, то при двукратном обходе кривой D -разбиения она оказывается два раза заштрихованной с одной стороны.
Приравняв нулю свободный член характеристического уравнения ( ), получаем уравнение особой прямой, соответствующей значению
), получаем уравнение особой прямой, соответствующей значению 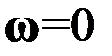 :
:  . Приравняв нулю коэффициент при старшем члене характеристического уравнения
. Приравняв нулю коэффициент при старшем члене характеристического уравнения  , получим уравнение особой прямой, соответствующей значению
, получим уравнение особой прямой, соответствующей значению  :
:  . Это будет прямая, совпадающая с осью ординат
. Это будет прямая, совпадающая с осью ординат  . Особые прямые, соответствующие значениям
. Особые прямые, соответствующие значениям  и
и  , следует штриховать так, чтобы вблизи этой точки, одновременно заштрихованные или одновременно не заштрихованные стороны кривой D -разбиения и особой прямой расположились навстречу друг другу.
, следует штриховать так, чтобы вблизи этой точки, одновременно заштрихованные или одновременно не заштрихованные стороны кривой D -разбиения и особой прямой расположились навстречу друг другу.
Претендующими на область устойчивости оказались две области А и В. Поскольку параметры  и
и  должны быть положительными, то областью устойчивости может быть лишь одна область, ограниченная кривой D -разбиения и положительными направлениями осей
должны быть положительными, то областью устойчивости может быть лишь одна область, ограниченная кривой D -разбиения и положительными направлениями осей  и
и  , показанная на рис. 1.2,б в другом масштабе.
, показанная на рис. 1.2,б в другом масштабе.






