Выполнил студент гр. СТ-15 Петров А.И

ЗАДАНИЕ 2: Численное решение дифференциального

Уравнения второго порядка методом Рунге-Кутта

Постановка задачи

 

Решить численно дифференциальное уравнение второго порядка с заданными начальными условиями для , шагом (табл. 1) и числе шагов методом Рунге-Кутта. Построить график зависимости с помощью программы Excel.

 

Содержание отчета

 

1. Постановка задачи для конкретного варианта.

2. Текст программы.

3. График зависимости , построенный с использованием программы Excel.

Методические указания

 

Результаты вычислений помещаются в файл rez.txt. При открытии данного файла с помощью программы Excel использовать опции мастера текстов, указанные ниже.

 

 

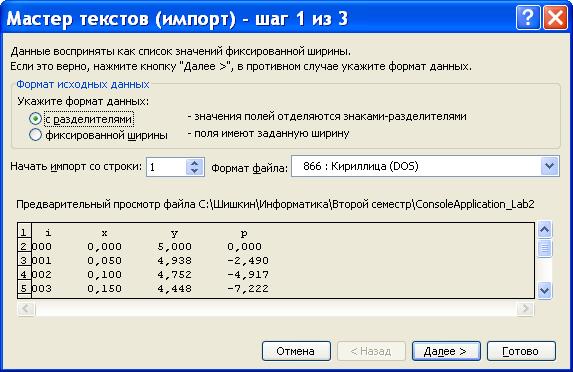
Варианты задания

Табл. 1.

Вариант	Дифференциальное уравнение
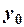
					0,01
					0,01
					0,01
					0,016
					0,01
					0,016
					0,02
					0,01
					0,01
					0,01
				-50	0,0125
					0,01
					0,01
					0,0125
					0,008

 

Теория метода Рунге-Кутта

 

Метод Рунге-Кутта является одним из численных методов повышенной точности. Сначала рассмотрим данный метод на примере дифференциального уравнения первого порядка. Пусть имеется уравнение

(1)

с начальным условием . В методе Рунге-Кутта приращение функции на шаге интегрирования содержит величину до четвертой степени включительно:

. (2)

Поэтому данный метод имеет четвертый порядок точности.

Вместо вычисления 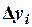непосредственно по формуле (2) в методе Рунге-Кутта предварительно определяются четыре числа:

(3)

Эти числа дают 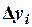с точностью до :

. (4)

Таким образом, получается алгоритм:

. (5)

Метод Рунге-Кутта можно использовать и для решения уравнений более высокого порядка. Рассмотрим уравнение второго порядка

(6)

с начальными условиями 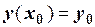, . Данное уравнение можно заменить системой двух дифференциальных уравнений 1-го порядка:

(7)

Для интегрирования этой системы вычисляются приращения:

(8)

где

(9)

Таким образом, получается алгоритм:

(10)

 

Пример оформления отчета

Тема лабораторной работы: численное решение дифференциального

Уравнения второго порядка методом Рунге-Кутта

Вариант 24

Выполнил студент гр. СТ-15 Петров А.И.

 

1. Постановка задачи: решить численно дифференциальное уравнение второго порядка с начальными условиями и шагом при числе шагов методом Рунге-Кутта. Построить график зависимости с использованием программы Excel..

2. Текст программы:

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

using System.IO;

 

namespace ConsoleApplication_Lab2

{

class Program

{

 

static void Main(string[] args)

{

int i, n = 121;

double[] x = new double[n];

double[] y = new double[n];

double[] p = new double[n];

double K1, K2, K3, K4, L1, L2, L3, L4, h = 0.05;

 

FileStream u = new FileStream("rez.txt", FileMode.Create);

StreamWriter Wr = new StreamWriter(u);

 

// Задание начальных условий

x[0] = 0;

y[0] = 5;

p[0] = 0;

 

// Шаговое интегрирование дифференциального уравнения y"+10y=0

for (i = 0; i < n - 1; i++)

{

K1 = h * p[i];

L1 = h * f(x[i], y[i], p[i]);

K2 = h * (p[i] + L1 / 2);

L2 = h * f(x[i] + h / 2, y[i] + K1 / 2, p[i] + L1 / 2);

K3 = h * (p[i] + L2 / 2);

L3 = h * f(x[i] + h / 2, y[i] + K2 / 2, p[i] + L2 / 2);

K4 = h * (p[i] + L3);

L4 = h * f(x[i] + h, y[i] + K3, p[i] + L3);

y[i + 1] = y[i] + (K1 + 2 * K2 + 2 * K3 + K4) / 6;

p[i + 1] = p[i] + (L1 + 2 * L2 + 2 * L3 + L4) / 6;

x[i + 1] = x[i] + h;

}

Console.WriteLine("Дифференциальное уравнение решено: результаты находятся в файле rez.txt");

Console.ReadLine();

 

// Печать результатов

Wr.WriteLine(" i x y p");

for (i = 0; i < n; i++)

{

Wr.WriteLine("{0:D3} {1:F3} {2:F3} {3:F3}", i, x[i], y[i], p[i]);

}

 

Wr.Close();

u.Close();

}

 

// Подпрограмма вычисления правой части уравнения

static double f(double x, double y, double p)

{

return 0 * x - 10 * y + 0 * p;

}

}

}

График зависимости.