Пакет прикладных программ STATISTICA

Введение

Применение открытых информационных систем, рассчитанных на использование всего массива информации, доступной в данный момент обществу в определенной его сфере, позволяет усовершенствовать механизмы управления общественным устройством, способствует гуманизации и демократизации общества, повышает уровень благосостояния его членов. Процессы, происходящие в связи с информатизацией общества, способствуют не только ускорению научно-технического прогресса, интеллектуализации всех видов человеческой деятельности, но и созданию качественно новой информационной среды социума, обеспечивающей развитие творческого потенциала индивида.

Одно из направлений процесса информатизации современного общества является информатизация образования - процесс обеспечения сферы образования методологией и практикой разработки и оптимального использования современных или, как их принято называть, новых информационных технологий, ориентированных на реализацию психолого-педагогических целей обучения, воспитания. [1].

Процесс информатизации так же затронул и экономические отрасли. Их радикальное усовершенствование и приспособление к современным условиям стало возможным благодаря массовому использованию новейшей компьютерной и телекоммуникационной техники, формирование на ее основе высокоэффективных информационно-управленческих технологий. Средства и методы прикладной информатики используются в менеджменте и маркетинге. Новые технологии, основанные на компьютерной технике, требуют радикальных изменений организационных структур менеджмента, его регламента, кадрового потенциала, системы документации, фиксирования и передачи информации.

Информационная технология (ИТ) — это комплекс взаимосвязанных, научных, технологических, инженерных дисциплин, изучающих методы эффективной организации труда людей, занятых обработкой и хранением информации; вычислительную технику и методы организации и взаимодействия с людьми и производственным оборудованием, их практические приложения, а также связанные со всем этим социальные, экономические и культурные проблемы. Сами информационные технологии требуют сложной подготовки, больших первоначальных затрат и наукоемкой техники. Их введение должно начинаться с создания математического обеспечения, формирования информационных потоков в системах подготовки специалистов.

Информационные технологии прочно вошли в нашу жизнь. Применение ЭВМ стало обыденным делом, хотя совсем ещё недавно рабочее место, оборудованное компьютером, было большой редкостью. Информационные технологии открыли новые возможности для работы и отдыха, позволили во многом облегчить труд человека.

Современное общество вряд ли можно представить без информационных технологий. Перспективы развития вычислительной техники сегодня сложно представить даже специалистам. Однако, ясно, что в будущем нас ждет нечто грандиозное. И если темпы развития информационных технологий не сократятся (а в этом нет никаких сомнений), то это произойдет очень скоро [2].

Значимость применения ИТ будет рассмотрено в данной работе на примере подготовки магистерской диссертации по теме «Оптимизация режимов дублирования костюмных тканей» (на примере ОАО «Знамя индустриализации» г. Витебск.)

Проблема применения информационных технологий является одной из наиболее актуальных. Именно здесь сосредоточены ресурсы дальнейшего развития по всем направлениям научно-технического прогресса. Очевидно, что швейная промышленность не могли остаться в стороне от использования информационных технологий в своих исследованиях[2].

Пакет прикладных программ STATISTICA.

В магистерской работе обработку результатов с определением числовых характеристик переменных проводила с использованием прикладных программ STATISTICA.

Система STATISTICA содержит исчерпывающий набор аналитических процедур в области добычи данных, науки и промышленного производства. Она позволяет строить различные графики, эффективно управлять данными и разрабатывать собственные приложения.

STATISTICA не только включает в себя универсальные статистические, графические процедуры и средства управления данными, но также реализует специализированные методы анализа данных (например, для добычи данных, бизнеса, социальных наук, медицинских исследований, инженерных приложений).

Все аналитические инструменты STATISTICA доступны как отдельные компоненты единого интегрированного пакета. Управлять ими можно различными способами: через пользовательский интерфейс или с помощью стандартного языка программирования SVB.

Интерфейс пользователя легко настраивается, а язык SVB позволяет автоматизировать задачи любой сложности. Применяя язык программирования, вы можете как избавить себя от рутинной работы с данными, так и упростить работу сложных масштабных проектов (например, интегрировать систему STATISTICA с другими приложениями или даже с большой корпоративной системой).

Уникальные возможности

Вот лишь некоторые уникальные возможности системы STATISTICA:

• широкий выбор аналитических процедур и их исчерпывающая реализация:

• набор качественных, настраиваемых по желанию пользователя графиков, дополняющих каждую вычислительную процедуру:

• эффективный и дружественный пользовательский интерфейс:

• интегрированный стандартный язык программирования SVB. добавляющий более 10000 новых функций к стандартному синтаксису Microsoft Visual Basic:

• большой набор технологий программного обеспечения (см. Используемые технологии программного обеспечения ниже), которые позволяют системе STATISTICA обрабатывать практически неограниченные объемы данных, достигать очень высокой производительности и поддерживать разнообразные опции настройки.

Одна из наиболее важных особенностей системы STATISTICA заключается в том, что подобные технологии позволяют даже новичку приспособить работу системы в соответствии со своими предпочтениями. Вы можете настроить практически каждый элемент STATISTICA. включая детали интерфейса.

С одной и той же версией STATISTICA могут работать:

• Начинающие пользователи, не искушенные в анализе данных. Они имеют возможность решать типовые задачи, принимая стартовые установки по умолчанию во всех диалоговых окнах анализов (используя, например, вкладку Быстрый) или даже работая со STATISTICA через обычный Web-браузер.

• Опытные аналитики, ученые и разработчики программ, которые могут интегрировать любую оптимизированную процедуру системы STATISTICA (более 10 ООО функций) в пользовательское приложение или вычислительную среду, используя объектно-ориентированные технологии и Web-технологии.

Вычисление параметров аппроксимирующей формулы на ЭВМ с использованием пакета прикладных программ «STATISTICA for WINDOWS».Корреляционный анализ. Проведение корреляционного анализа позволяет ответить на вопрос: имеется ли вообще какая-либо статистическая связь между исследуемым показателем качества и управляемым фактором и какова теснота этой связи?

Для оценки тесноты связи между двумя любыми количественными переменными используется парный коэффициент корреляции, отражающий тенденцию взаимного изменения переменных.

Для проведения корреляционного анализа в первую очередь создайте в имеющейся уже таблице дополнительно два столбца, содержащие необходимые данные: значения управляемого фактора x_j (температуры прессования) и соответствующие им среднеарифметические значения исследуемого показателя качества 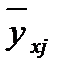(продолжительность дублирования).

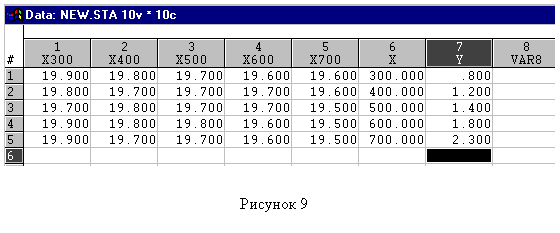
Столбец, который будет содержать пять значений температуры прессования, обозначьте в шапке таблицы буквой Х; столбец со средними значениями продолжительности дублирования – буквой Y, и введите данные (рисунок 1.1).

Рисунок 1.1

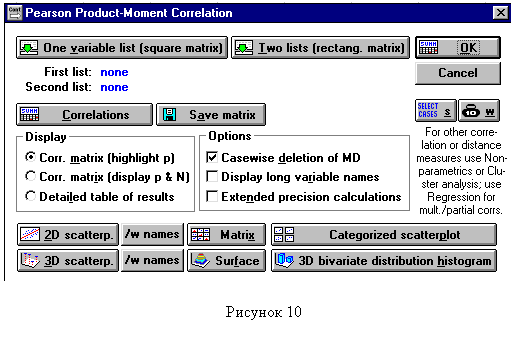
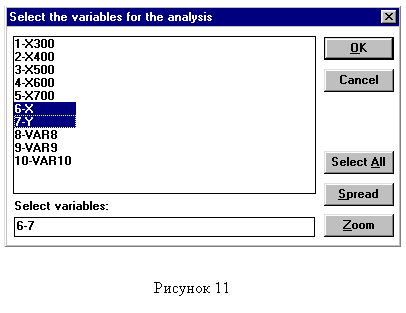
Теперь в меню нажмите «Analysis» и выберите раздел «Correlation matrices». В окне (рисунок 1.2) требуется нажать «One variable list (square matrix)» и определить, наличие связи между значениями каких столбцов будем устанавливать. Выделите столбцы Х и Y путем одновременного нажатия левой клавиши мыши и клавиши «Shift» на клавиатуре (рисунок 1.3).

Рисунок 1.2	Рисунок 1.3

После нажатия последовательно в двух открытых окошках «ОК» получим рассчитанные парные коэффициенты корреляции (рисунок 1.4), расположенные в ячейках на пересечении Х и Y (нижняя слева и верхняя справа). Если парные коэффициенты выделены красным цветом, значит для них уровень значимости не превышает 0,05. Уровень значимости характеризует вероятность событий, условно принимаемых за невероятные, т.е. чем ниже его величина, тем достоверней результат. Уровень значимости в 5% (0,05) соответствует доверительной вероятности 95 %.

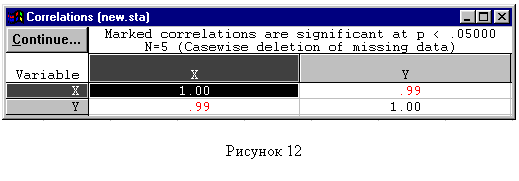
Рисунок 1.4

Коэффициент корреляции может быть как положительным, так и отрицательным. Знак «-» перед коэффициентом указывает на наличие обратной связи между показателем качества и фактором, от которого он зависит.[3]

Регрессионный анализ. Метод регрессионного анализа (метод наименьших квадратов) позволяет математически описать связь между независимой переменной Х и зависимой величиной Y и найти функцию Y=f(Х).

Линейный регрессионный анализ. Для проведения линейного однофакторного регрессионного анализа необходимо войти в переключатель разделов «STATISTICA Module Switcher». Для этого нажмите в меню «Analysis» и выберите «Other Statistics». В появившемся переключателе разделов выберите «Multiple Regression» или «Linear Regression» (рисунок1.5).

Для того чтобы использовать для дальнейшей работы данные таблицы из «Basic Statistics and Tables» в «Multiple Regression», в открывшемся окне нажмите клавишу «Yes».

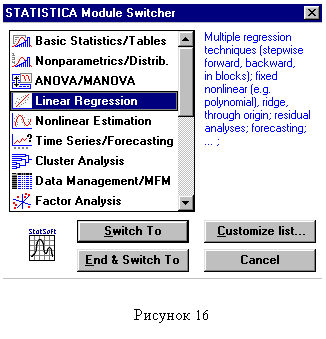
Рисунок 1.5

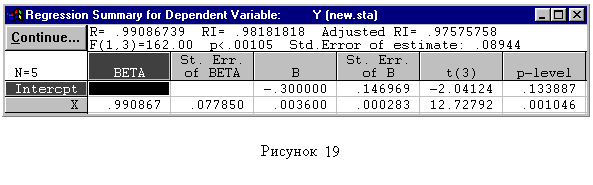
В появившемся окне «Multiple Regression», во-первых, необходимо нажать «Variables» и определить зависимую «Dependent» (в первом столбце выделите Y) и независимую «Independent» (во втором столбце выделите Х) переменные, для которых необходимо построить регрессионную модель (рисунок 1.6).Если случилось так, что с экрана исчезло окно «Multiple Regression», либо вы изменили какие-либо значения в столбцах X или Y уже находясь непосредственно в разделе «Multiple Regression», открыть снова окно «Multiple Regression» можно войдя в меню «Analysis» и выбрав «Resume Analysis».Далее последовательно в двух окнах нажмите «ОК» и на появившемся экране «Multiple Regression Results» (рисунок 1.7) нажмите «Regression summary». Искомые данные будут находиться в окне-таблице «Regression Summary for Dependent Variable» (рисунок1.8) в столбце «В» (коэффициенты модели), причем первым будет свободный коэффициент «Intercept». В последнем столбце указывается уровень значимости коэффициента. Коэффициенты с уровнем значимости более 0,05 (p-level >0,05) включать в модель нецелесообразно. В линейной модели таковым может оказаться свободный коэффициент. Для получения абсолютно точного уравнения необходимо сключить незначимые коэффициенты и повторить расчет. Если требуется получить модель без свободного коэффициента, то надо закрыть открытые окна путем нажатия на «X» и клавишу «Cancel» и вернуться в окно «Model Definition» (рисунок 1.9). В поле «Intercept» необходимо заменить «Include in model» (включить в модель) на «Set to zero» (приравнять нулю) и вновь произвести расчет.

 

 

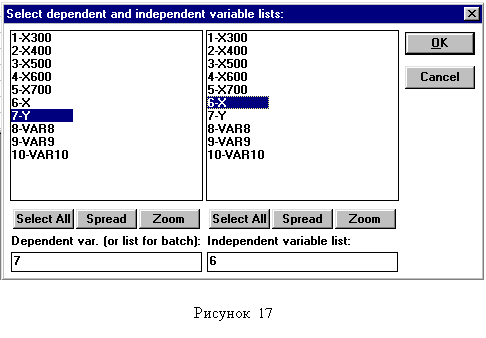
Рисунок 1.6
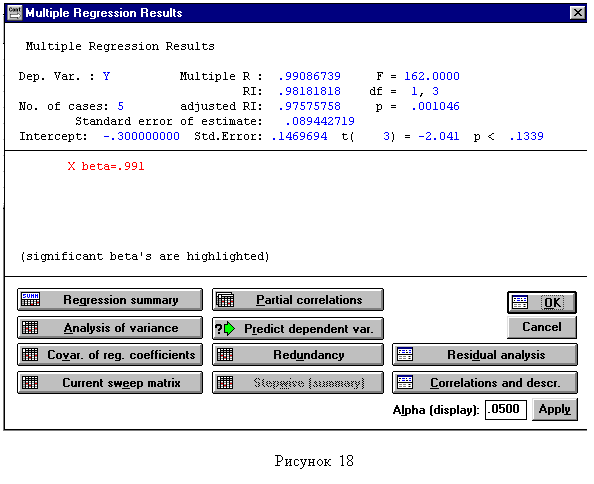
Рисунок 1.7
Рисунок 1.8
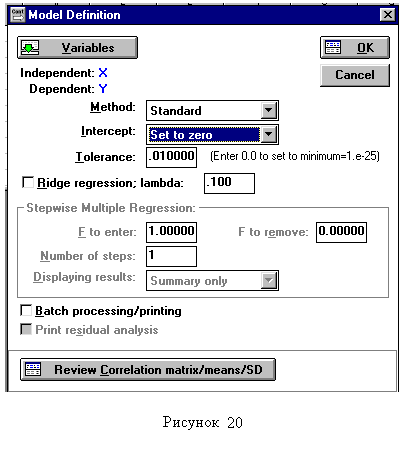
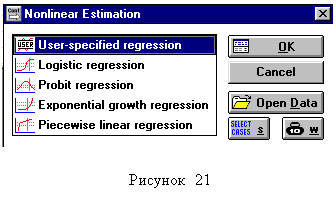
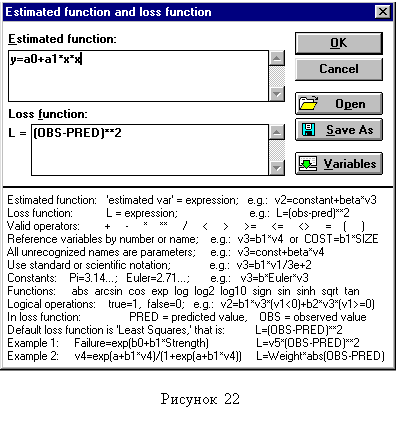
	Нелинейный регрессионный анализ. Для проведения нелинейного регрессионного анализа необходимо вернуться в переключатель разделов «STATISTICA Module Switcher» (см. ранее), выбрать раздел «Nonlinear Estimation», а затем «User-specified regression» (рисунок 1.10). Далее требуется нажать «Function to be estimated & loss function» (рассчитываемая функция и функция оценки отклонения) и определить в поле «Estimated function» (рисунок1.11) уравнение, для которого необходимо произвести расчет коэффициентов.
Рисунок1.9
Рисунок1.10	Рисунок 1.11

Ввод уравнений и расчет коэффициентов необходимо производить поочередно для параболической и гиперболической функций:

- парабола y=а0+а1*x+а2*x*х;

- гипербола y=а0+а1/x.

При введении уравнения прямой y=а0+а1*x

можно в этом же разделе выполнить линейный регрессионный анализ.

После введения формулы на всех последующих окнах нужно просто нажимать «ОК», пока не появится окно-таблица «Model» (рисунок 1.12).

При оценке полученной модели следует придерживаться рекомендаций, приведенных в разделе «Линейный регрессионный анализ». При наличии коэффициента, уровень значимости которого превышает 0,05, необходимо вернуться в окно «User-specified regression» (рисунок 1.13), нажать «Function to be estimated & loss function», удалить слагаемое, содержащее незначимый коэффициент и повторить расчеты.

 

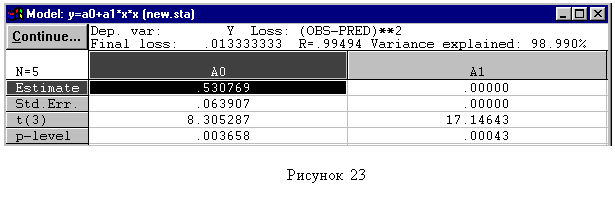
Рисунок 1.12
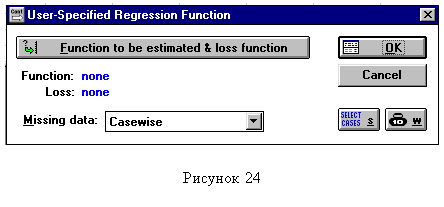
Рисунок 1.13

После установления окончательного вида модели можно вывести на экран графическое изображение функциональной зависимости. Для этого в окне «Results» (рисунок 1.14), которое предшествует окну-таблице

«Model», нажмите на «Fitted 2D function & observed vals». В полученном окне (рисунок 1.15) содержится следующая информация:

- общий вид уравнения: например, для параболы y=a0+a1*x*x;

- окончательный вид уравнения: y=(0,5307692)+(3,589744е-006)*х*х, где е-006 должно расцениваться как 10^-6;

- точки экспериментальной зависимости, обозначенные синими кружочками и буквами С;

- график теоретической зависимости.

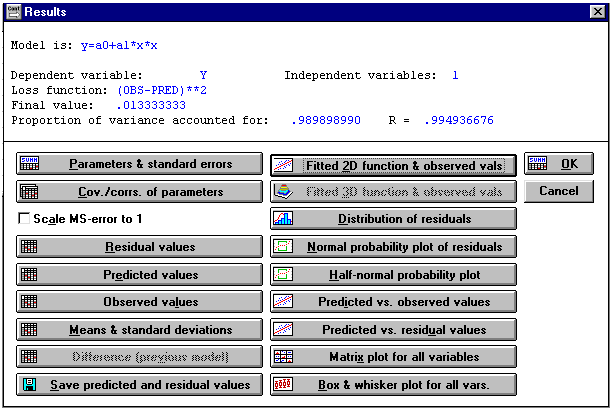
Рисунок 1.14
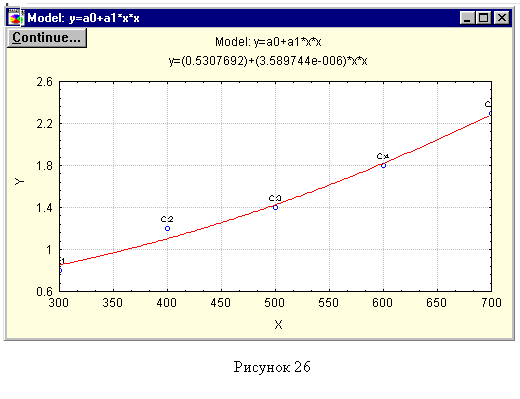
Рисунок 1.15