Програмові вимоги - 2012
(освітньо-кваліфікаційний рівень - бакалавр)
Спеціальність “Прикладна математика”
Математичний аналiз
1. Множина дійсних чисел. Упорядкованість, щільність, повнота множини дійсних чисел.
2. Числова послідовність. Види числових послідовностей. Границя послідовності. Властивості збіжних послідовностей.
3. Нескінченно малі і нескінченно великі послідовності, співвідношення між ними. Леми про нескінченно малі. Границя алгебраїчної суми, добутку, частки.
4. Відповідність, відображення, функція. Способи задання. Види функцій.
5. Границя функції в розумінні Гейне та Коші. Еквівалентність означень. Визначні границі: 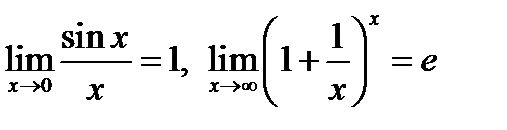 .
.
6. Неперервність функції в точці. Різні означення. Одностороння неперервність і її зв’язок з неперервністю в точці. Властивості неперервної функції на сегменті. Теореми Больцано-Коші, Вейєрштраса, Кантора.
7. Задачі, які приводять до поняття похідної. Означення похідної. Таблиця похідних. Геометричний та механічний зміст. Правила відшукання похідних. Похідна композиції функцій.
8. Застосування похідної до дослідження функції на сталість, монотонність.
9. Локальний екстремум функції. Необхідна умова. Достатні умови. Знаходження найбільшого і найменшого значення функції на сегменті.
10. Напрям опуклості графіка функції. Достатні умови. Точка перегину. Необхідна умова перегину. Достатні умови.
11. Первісна функція (неозначений інтеграл). Таблиця основних інтегралів. Інтегруваня підстановкою, частинами.
12. Інтеграл Рімана. Необхідна умова. Необхідна і достатня умова інтегрованості. Класи інтегрованих функцій. Теорема Ньютона-Лейбніца.
13. Основні застосування інтеграла Рімана (знаходження площ, об’ємів, довжин дуг; площ поверхонь обертання; фізичні застосування).
14. Функції багатьох змінних. Границя, неперервність. Властивості неперервних функцій.
15. Частинні похідні, диференційованість функції багатьох змінних. Достатня умова диференційованості. Диференціал функції. Правила диференціювання.
16. Числові ряди. Збіжні числові ряди. Необхідна умова збіжності. Необхідна і достатня умова збіжності. Ознаки збіжності додатних рядів.
Література:
1. М.І. Шкіль. Математичний аналіз. Т.1,2. К: Вища школа.
2. Г.Ф. Фихтенгольц. Основы математического анализа. Т.1,2. (будь-яке видання).
3. В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Т.1,2. М.: Наука.
4. Л.Д. Кудрявцев. Математический анализ. Т.1,2. М.: Высшая школа.
Диференціальні рівняння.
Диференціальні рівняння першого порядку:
Однорідні рівняння та звідні до них.
Рівняння в повних диференціалах. Інтегрувальний множник.
Лінійні рівняння та звідні до них.
Рівняння, не розв’язані відносно похідної.
Лінійні диференціальні рівняння вищих порядків.
Рівняння, які інтегруються у квадратурах. Рівняння, які допускають зниження порядку.
Лінійні однорідні рівняння зі сталими коефіцієнтами.
Лінійні неоднорідні рівняння (методи варіації довільних сталих, невизначених коефіцієнтів).
Лінійні рівняння зі змінними коефіцієнтами.
Література:
1. Шкіль М.І., Лейфура В.М., Самусенко П.Ф. Диференціальні рівняння. – К.: Техніка, 2003.
2. Самойленко А.М., Перестюк М.О., Парасюк І.О. Диференціальні рівняння. – К.: Либідь, 2003.
3. Кривошея С.А., Перестюк М.О., Бурим В.М. Диференціальні та інтегральні рівняння. – К.: Либідь, 2004.
4. Лавренюк С.П. Курс диференціальних рівнянь. – Львів: Вид-во наук.-техн. л-ри, 1997.
5. Гой Т.П., Казмерчук А.І., Федак І.В. Звичайні диференціальні рівняння (Частина 1. Диференціальні рівняння першого порядку, які інтегруються у квадратурах). – Івано-Франківськ: ЛІК, 2005.
6. Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1977.
Рівняння з частинними похідними
1. Рівняння математичної фізики. Класифікація лінійних рівнянь другого порядку в точці.
2. Постановка основних крайових задач. Коректність задач.
3. Задача Коші для рівняння струни. Формула Даламбера.
4. Метод відбиття в задачах для півобмеженої і обмеженої струни.
5. Метод Фур’є розв’язання крайових задач для рівнянь струни і теплопровідності.
Література:
1. Перестюстюк М.О., Маринець В.В. Теорія рівнянь математичної фізики.
2. Іванчов М.І. Вступ до теорії рівнянь у частинних похідних.
3. Михлин С.Г. Уравнения математической физики.
4. Владимиров В.С. Уравнения математической физики.
5. Тихонов А.Н., Самарский А.А. Уравнения математической физики.
6. Петровский М.Г. Лекции об уравнениях с частными производными.
7. Михайлов В.П. Дифференциальные уравнениях в частных производных.
8.
Чисельні методи
1. Уточнення наближених значень коренів рівняння f (x) = 0 методами хорд, дотичних, комбінованим методом хорд та дотичних. Геометрична ілюстрація. Блок-схеми методів.
2. Уточнення наближених значень коренів рівняння f (x) = 0 методом ітерацій. Геометрична ілюстрація. Блок-схема методу. Достатня умова збіжності методу ітерацій. Оцінка похибки.
3. Класифікація методів розв’язування систем лінійних алгебраїчних рівнянь. Точні методи розв’язування СЛАР. Розв’язування СЛАР методом Гауса. Уточнення розв’язків, одержаних цим методом.
4. Розв’язування систем лінійних алгебраїчних рівнянь методом ітерацій. Достатня умова збіжності методу. Оцінка наближення.
5. Розв’язування систем нелінійних рівнянь методом Ньютона.
6. Постановка задачі інтерполяції. Геометрична ілюстрація. Інтерполяційні многочлени Лагранжа і Ньютона. Оцінка похибок.
7. Постановка задачі чисельного диференціювання. Чисельне диференціювання на основі інтерполяційних формул Лагранжа, Ньютона. Оцінка похибки.
8. Постановка задачі чисельного інтегрування. Чисельне інтегрування функції методами прямокутників, трапеції, парабол (Сімпсона). Похибки цих методів.
9. Метод Ейлера та його модифікації розв’язування задачі Коші для звичайних диференціальних рівнянь першого порядку. Розрахункові формули. Геометрична ілюстрація. Блок схеми.
Література
1. М.Я.Лященко, М.С.Головань. Чисельні методи. – К., Либідь, 1976. – 368 с
2. Цегелик Г. Чисельні методи. – Львів: Видавничий центр ЛНУ ім. І. Франка, 2004. – 408 с.
3. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М., Наука, 1970. –
664 с.
Методи оптимізації і дослідження операцій
1. Задача лінійного програмування (ЛП): постановки, властивості, геометричне тлумачення, графічний метод.
2. Теоретичні основи симплексного методу розв'язування задач ЛП.
3. Теорія двоїстості в ЛП: поняття і правила побудови двоїстих задач, основні теореми двоїстості.
4. Теоретичні основи двоїстого симплекс-методу розв'язування задач ЛП.
5. Постановка і властивості транспортної задачі ЛП за критерієм вартості. Методи побудови початкового опорного плану.
6. Теоретичні основи методу потенціалів розв'язування транспортної задачі.
7. Цілочислова задача ЛП. Загальна ідея методів відтинання. Алгоритми методу Гоморі.
8. Задача дробово-лінійного програмування. Графічний метод і зведення до задачі ЛП.
9. Задачі оптимізації з обмеженнями типу рівностей. Метод множників Лагранжа.
10. Найпростіша задача варіаційного числення та її узагальнення.
11. Задача Больца та її узагальнення.
Література:
1. Цегелик Г.Г. Лінійне програмування. - Львів: в-во Світ, 1998. - 215 с.
2. Попов Ю.Д., Тюптя В.І., Шевченко В.І. Методи оптимізації. - К., 2003. - 215 с.
3. Зайченко Ю.П. Дослідження операцій. - 7-е вид. - К.: Слово, 2006. - 816 с.
4. Степанюк В.В. Методи математичного програмування. - К.: Вища школа, 1977. - 272 с.
5. Моклячук М.П. Варіаційне числення. Екстремальні задачі. - К., 2003. - 380 с.
Алгебра та геометрiя
1. Різні способи задання прямих та площин в просторі. Взаємне розміщення двох прямих, прямої та площини.
2. Векторний і мішаний добутки. Їх властивості і застосування.
3. Лiнiйна залежнiсть та ранг системи векторiв.
4. Векторний простір, його розмірність і базис. Підпростори, теорема про суму їх розмірностей.
5. Лiнiйнi оператори дійсних векторних просторiв, їх матрицi, ранг і дефект.
6. Власнi вектори та власнi числа лiнiйних операторiв.
7. Ортогональні перетворення площини і їх застосування до спрощення рівнянь кривих ІІ порядку.
Література:
1. Білоусова В.П. і ін. Аналітична геометрія К., Вища школа, 1973.
2. Завало А.В. Курс алгебри. Київ, Вища школа, 1986.
3. Курош А.Г. Курс высшей алгебры. -., Наука, 1965.- 471с.
4. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре.- М., Наука, 1964.-304с.
Програмування
1. Мови програмування, їхня класифікація та опис мови.
2. Програми користувача: підпрограми.
3. Оператори умови та їх використання.
4. Типи даних: масиви, рядки.
5. Оператори циклу та їх використання.
6. Процедури і функції роботи з файлами.
7. Основні поняття об’єктно-орієнтованого програмування.
8. Поняття про наслідування та інкапсуляцію.
9. Механізми підтримки поліморфізму.
Література
1. Зуєв Е. А. Язык программирования TURBO- PASCAL 6.0. Москва, Унитех, 1992
2. Вальвачев А. Н., Крисевич В. С. Программирование на языке Паскаль для персональных ЭВМ. Минск: Высш. Школа,1989.
3. Климов Ю. С., Касаткин Л. И., Мороз С. М Программирования в среде TURBO- PASCAL 6.0.
4. Себеста Р. Основные концепции языков программирования.- М., Издательский дом «Вильямс», 2000.
5. Вирт Н. Алгоритмы + Структуры данных = Програмы. -М., Мир, 1984
База даних та інформаційні системи
1. Поняття бази і банку даних та їх складових.
2. Поняття СУБД, її функцій та мовні засоби роботи з даними.
3. Етапи проектування баз даних.
4. Поняття інфологічної моделі та її складові.
5. Поняття агрегації та порядок її виконання.
6. Представлення запитів в структурованому вигляді відповідним запитувальним зв’язком.
7. Теорія нормалізації відношень.
8. Особливості та переваги мови SQL.
9. Групи команд мови SQL та їх приклади.
Література:
1. Н.В. Єрьоміна. Проектування баз даних: Навч. посібник. – К.:КНЕУ,1998. – 208с.
2. Н.В. Ситник. Проектування баз і сховищ даних: Навч. посібник. – К.: КНЕУ, 2004.-348с.
3. Конноли Томас, Каролин Бегг, Страчан Анна. Базы данных: проэктирование, реализация и сопровождение. Теория и практика, 2-е изд.,: Пер. с англ. – Изд. Дом “Вильямс”, 2001. – 1120с.
4. К.Дейт, Введение в системы БД. Москва,-Санкт-Петербург,- Киев, 2000
5. Дж.Грофф, П.Вайнберг, SQL: Полное руководство. К.: BHV, 2001.- 814 с.
6. Клименко Н.Р., Головко О.Д., Шарапова О.Д., Інформатика та комп’ютерна техніка. Навч.- метод.-посіб. К.: КНЕУ, 2002.- 534с.






