Теоретическая часть
Этьен Безу
Этьен Безу - французский математик, член Парижской Академии Наук (с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года.
С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.
Основные работы Этьена Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений. В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную К. Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в m n точках. Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный «Курс математики», написанный им в 1764-69 годах. Безу развил метод неопределённых множителей, в элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе. Часть трудов Безу посвящена внешней баллистике. Именем учёного названа одна из основных теорем алгебры.
Теорема Безу. Доказательство и следствия.
Остаток от деления полинома Pn(x) на двучлен (x-a) равен значению
этого полинома при x = a.
Пусть:
Pn(x) – данный многочлен степени n,
двучлен (x-a) - его делитель,
Qn-1(x) – частное от деления Pn(x) на x-a (многочлен степени n-1),
R – остаток от деления (R не содержит переменной x как делитель первой степени относительно x).
Доказательство:
Согласно правилу деления многочленов с остатком можно записать:
Pn(x) = (x-a)Qn-1(x) + R.
Отсюда при x = a:
Pn(a) = (a-a)Qn-1 (a) + R =0*Qn-1(a)+R=0+R=R.
Значит, R = Pn(a), т.е. остаток от деления полинома на (x-a) равен значению этого полинома при x=a, что и требовалось доказать.
Следствия из теоремы
С ледствие 1:
Остаток от деления полинома Pn (x) на двучлен ax+b равен значению этого полинома при x = -b/a, т. е. R=Pn (-b/a).
Доказательство:
Согласно правилу деления многочленов:
Pn(x)= (ax + b)* Qn-1 (x) + R.
При x= 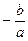 :
:
Pn (-b/a) = (a(-b/a) + b)Qn-1(-b/a) + R = R. Значит, R = Pn (-b/a), что и требовалось доказать.
Следствие 2:
Если число a является корнем многочлена P (x), то этот
Многочлен делится на (x-a) без остатка.
Доказательство:
По теореме Безу остаток от деления многочлена P (x) на x-a равен P (a), а по условию a является корнем P (x), а это значит, что P (a) =0, что и требовалось доказать.
Из данного следствия теоремы Безу видно, что задача решения уравнения P (x) = 0 равносильна задаче выделения делителей многочлена P, имеющих первую степень (линейных делителей).
Следствие 3:
Если многочлен P (x) имеет попарно различные корни
a1, a2, …, an, то он делится на произведение (x-a1) … (x-an)
без остатка.
Доказательство:
Проведём доказательство с помощью математической индукции по числу корней. При n=1 утверждение доказано в следствии 2. Пусть оно уже доказано для случая, когда число корней равно k, это значит, что P(x) делится без остатка на (x-a1)(x-a2) … (x-ak), где
a1, a2, …, ak - его корни.
Пусть P(x) имеет k+1 попарно различных корней. По предположению индукции a1, a2, ak, …, ak+1 являются корнями многочлена, а, значит, многочлен делится на произедение (x-a1) … (x-ak), откуда выходит, что
P(x) = (x-a1) … (x-ak)Q(x).
При этом ak+1 – корень многочлена P(x), т. е. P(ak+1) = 0.
Значит, подставляя вместо x ak+1, получаем верное равенство:
P(ak+1) = (ak+1-a1) … (ak+1-ak)Q(ak+1) = 0
Но ak+1 отлично от чисел a1, …, ak, и потому ни одно из чисел ak+1-a1, …, ak+1-ak не равно 0. Следовательно, нулю равно Q(ak+1), т. е. ak+1 – корень многочлена Q(x). А из следствия 2 выходит, что Q(x) делится на x-ak+ 1 без остатка.
Q(x) = (x-ak+1)Q1(x), и потому
P(x) = (x-a1) … (x-ak)Q(x) = (x-a1) … (x-ak)(x-ak+1)Q1(x).
Это и означает, что P(x) делится на (x-a1) … (x-ak+1) без остатка.
Итак, доказано, что теорема верна при k =1, а из её справедливости при n = k вытекает, что она верна и при n = k+1. Таким образом, теорема верна при любом числе корней, что и требовалось доказать.
Следствие 4:
Многочлен степени n имеет не более n различных корней.
Доказательство:
Воспользуемся методом от противного: если бы многочлен Pn(x) степени n имел бы более n корней - n+k (a1, a2, …, an+k - его корни), тогда бы по ранее доказанному следствию 3 он
бы делился на произведение (x-a1) … (x-an+k), имеющее степень n+k, что невозможно.
Мы пришли к противоречию, значит, наше предположение неверно и многочлен степени n не может иметь более, чем n корней, что и требовалось доказать.
Следствие 5:




