Пусть функции 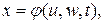
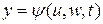 ,
, 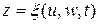 взаимно однозначно отображают область V в криволинейных координатах u,w,t.
взаимно однозначно отображают область V в криволинейных координатах u,w,t.
Пусть при этом элемент объема ∆Vi области V переходит в элемент ∆Vi′ области V′ и выполняется условие 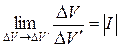 .
.
Определить I, называемый якобианом, численно равен определителю третьего порядка, который вычисляется по формуле:
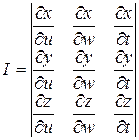
При выполнении этих условий
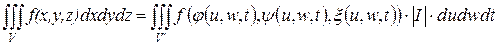 .
.
В случае цилиндрических координат имеем 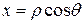 ,
, 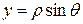 , z = z.
, z = z.
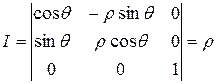 .
.
Для сферических координат 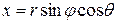 ,
, 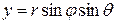 ,
, 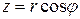 .
.
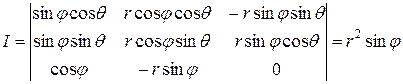 .
.
Пример выполнения расчетно-графической работы
Задача 1. Изменить порядок интегрирования.
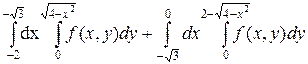
Решение. Изобразим область интегрирования на чертеже:
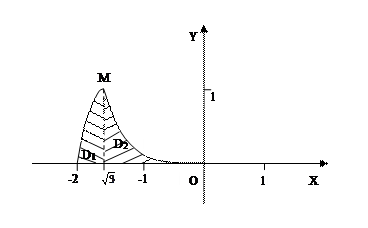
Область интегрирования D состоит из двух областей D1 и D2, D1 – ограничена линиями: прямыми 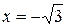 , y=0 и дугой окружности y=
, y=0 и дугой окружности y= 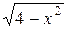 ; D2 ограничена прямыми
; D2 ограничена прямыми 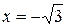 , y=0 и дугой окружности y=2-
, y=0 и дугой окружности y=2- 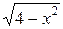 . Найдем точку пересечения окружностей М:
. Найдем точку пересечения окружностей М:
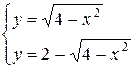
Приравнивая правые части уравнений системы, получим:
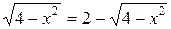 ; откуда
; откуда 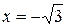 ; тогда
; тогда 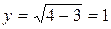 . Точка М имеет координаты
. Точка М имеет координаты 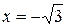 , y=1.
, y=1.
Изменяя порядок интегрирования, видим: y изменяется от 0 до 1. При этом x меняется от окружности x2+y2=4 до окружности y=2- 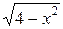 . Окончательно получим:
. Окончательно получим:
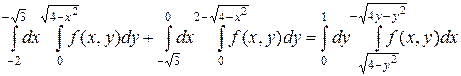 .
.
Задача 2. Вычислить двойной интеграл 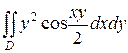 , где D: область, ограниченная линиями: x=0, y=
, где D: область, ограниченная линиями: x=0, y= 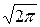 , y=2x.
, y=2x.
Решение. Изобразим область D:
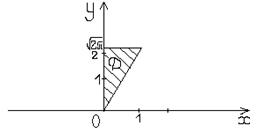
Анализируя область интегрирования, замечаем: x меняется от 0 до прямой  ; при этом y меняется от 0 до
; при этом y меняется от 0 до 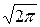 .
.
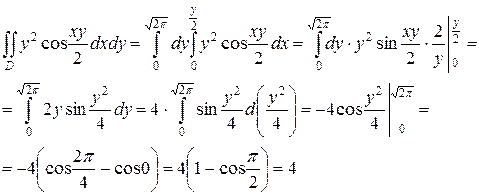
Ответ: 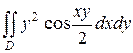 = 4.
= 4.
Задача 3. Найти площадь фигуры, ограниченной линиями: x2+y2=12, x 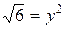 .
.
Решение. Изобразим данную фигуру:
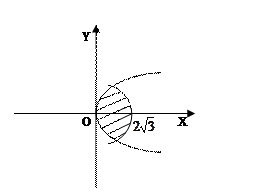
Найдем точки пресечения линий, ограничивающих данную фигуру:
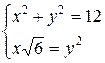 .
.
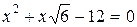 ;
;
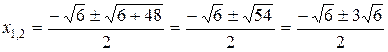 ;
;
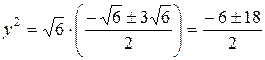 ;
;
y2=6;
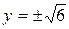 .
.
Площадь фигуры вычислим по формуле:
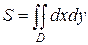 ;
;
Учитывая симметрию фигуры относительно оси OX, получим:
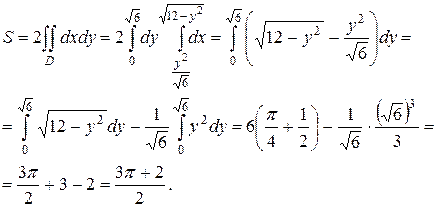
Ответ: S= 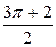 (ед2.)
(ед2.)
Задача 4. Вычислить 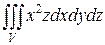 , V: y=3x, y=0, x=2, z=xy, z=0.
, V: y=3x, y=0, x=2, z=xy, z=0.
Решение.
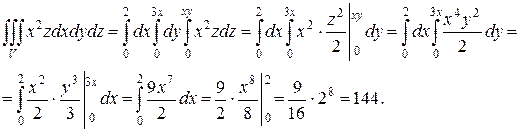
Ответ: 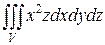 = 144.
= 144.
Задача 5. Пластинка D задана ограничивающими её кривыми, μ – поверхностная плотность. Найти массу пластинки.
D: 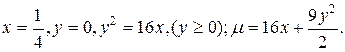
Решение. Масса пластинки m равна:
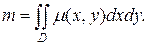
Подставляя данные задачи, получим:
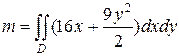
Изобразим область D:
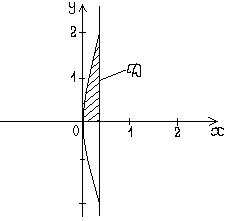
Расставляя пределы интегрирования в двойном интеграле, получим:
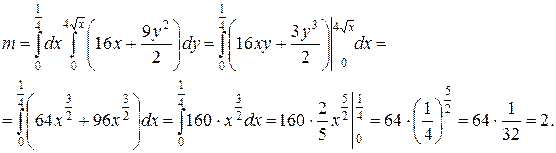
Ответ: m=2.
Задача 6. Найти объем тела, заданного ограничивающими его поверхностями:
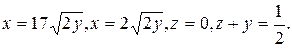
Решение. Объем тела V равен:
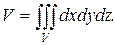
Переходя к повторному интегралу, получим:
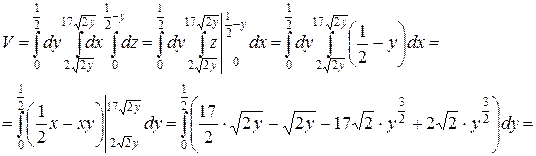
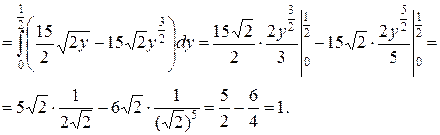
Ответ: V=1.
Варианты расчетно-графической работы
Задание 1. Изменить порядок интегрирования.
1. 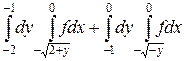 .
.
2. 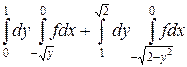 .
.
3. 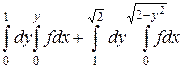 .
.
4. 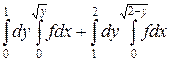 .
.
5. 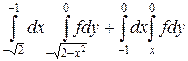 .
.
6. 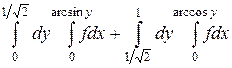 .
.
7.  .
.
8. 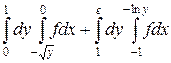 .
.
9. 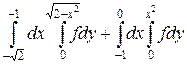 .
.
10. 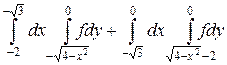 .
.
11. 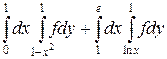 .
.
12. 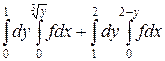 .
.
13. 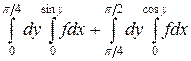 .
.
14. 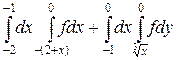 .
.
15. 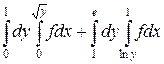 .
.
16. 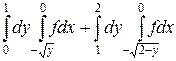 .
.
17. 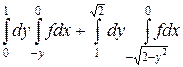 .
.
18. 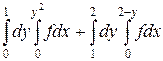 .
.
19. 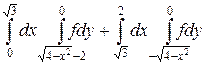 .
.
20. 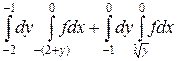 .
.
21. 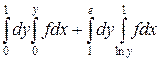 .
.
22. 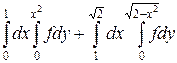 .
.
23. 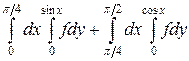 .
.
24. 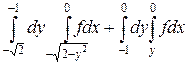 .
.
25. 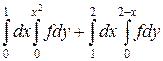 .
.
26. 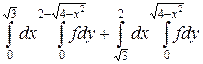 .
.
27. 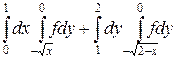 .
.
28.  .
.
29. 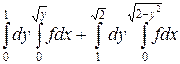 .
.
30. 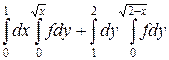 .
.
Задание 2. Вычислить двойной интеграл.
1. 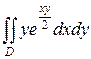 ;
; 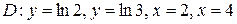 .
.
2. 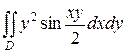 ;
; 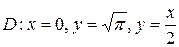 .
.
3. 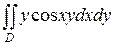 ;
; 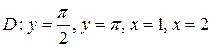 .
.
4. 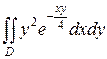 ;
; 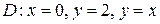 .
.
5. 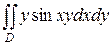 ;
; 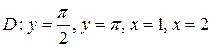 .
.
6. 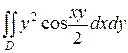 ;
; 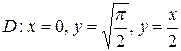 .
.
7. 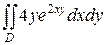 ;
; 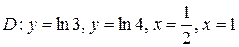 .
.
8. 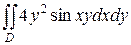 ;
; 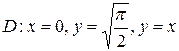 .
.
9. 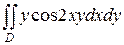 ;
; 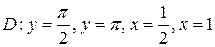 .
.
10. 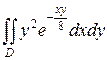 ;
; 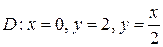 .
.
11.  ;
; 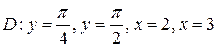 .
.
12. 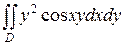 ;
; 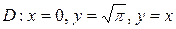 .
.
13. 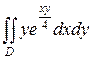 ;
; 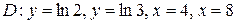 .
.
14. 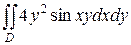 ;
; 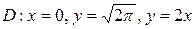 .
.
15. 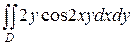 ;
; 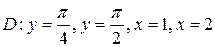 .
.
16. 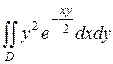 ;
; 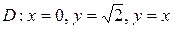 .
.
17. 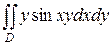 ;
; 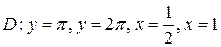 .
.
18. 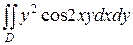 ;
; 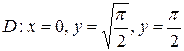 .
.
19. 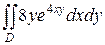 ;
; 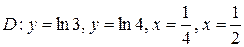 .
.
20. 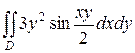 ;
; 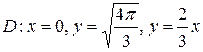 .
.
21. 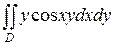 ;
; 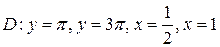 .
.
22. 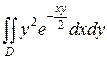 ;
; 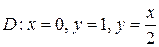 .
.
23. 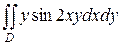 ;
; 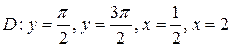 .
.
24. 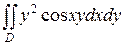 ;
; 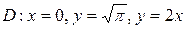 .
.
25. 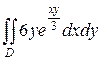 ;
;  .
.
26. 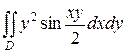 ;
; 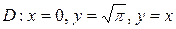 .
.
27. 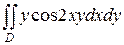 ;
; 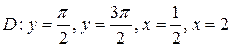 .
.
28. 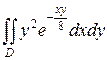 ;
; 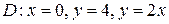 .
.
29. 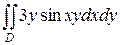 ;
; 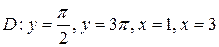 .
.
30. 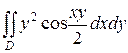 ;
; 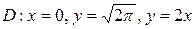 .
.
Задание 3. Найти площадь фигуры, ограниченной данными линиями.
1. 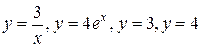 .
.
2. 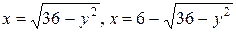 .
.
3. 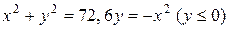 .
.
4. 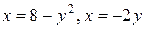 .
.
5. 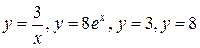 .
.
6. 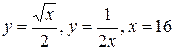 .
.
7. 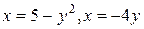 .
.
8. 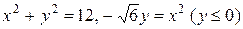 .
.
9. 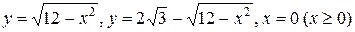 .
.
10. 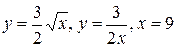 .
.
11. 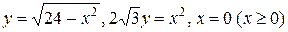 .
.
12. 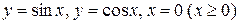 .
.
13. 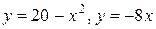 .
.
14. 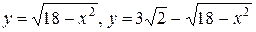 .
.
15. 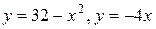 .
.
16. 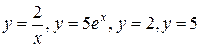 .
.
17. 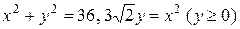 .
.
18. 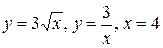 .
.
19. 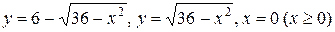 .
.
20. 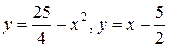 .
.
21. 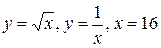 .
.
22. 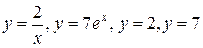 .
.
23. 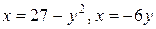 .
.
24. 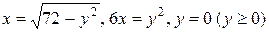 .
.
25. 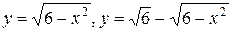 .
.
26. 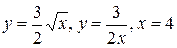 .
.
27. 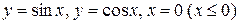 .
.
28. 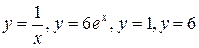 .
.
29. 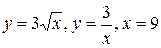 .
.
30. 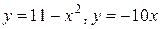 .
.
Задание 4. Пластинка D задана ограничивающими ее кривыми, m - поверхностная плотность. Найти массу пластинки.
1. 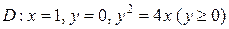 ;
; 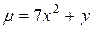 .
.
2. 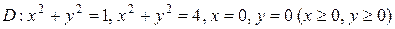 ;
; 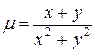 .
.
3. 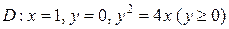 ;
; 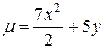 .
.
4. 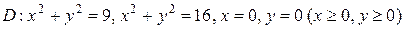 ;
; 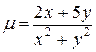 .
.
5. 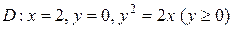 ;
; 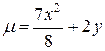 .
.
6. 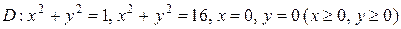 ;
; 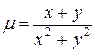 .
.
7. 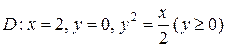 ;
; 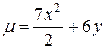 .
.
8. 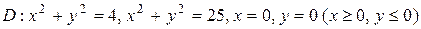 ;
; 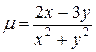 .
.
9. D: х=1, y=0, y2=4х (y 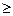 0);
0); 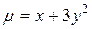 .
.
10. D: x2+y2=1, x2+y2=9, x=0, y=0 (x 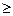 0, y
0, y 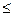 0);
0);  = (x-y)/(x2+y2).
= (x-y)/(x2+y2).
11. D: x=1, y=0, y2=x (y 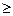 0);
0);  =3x+6y2.
=3x+6y2.
12. D: x2+y2=9, x2+y2=25, x=0, y=0 (x 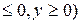 ;
;  =(2y-x)/(x2+y2).
=(2y-x)/(x2+y2).
13. D: x=2, y=0, y2=x/2 (y 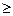 0);
0);  =2x+3y2.
=2x+3y2.
14. D: x2+y2=4, x2+y2=16, x=0, y=0 (x 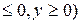 ;
;  =(2y-3x)/(x2+y2).
=(2y-3x)/(x2+y2).
15. D: x= 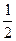 , y=0, y2=8x (y
, y=0, y2=8x (y 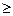 0);
0);  = 7x+3y2.
= 7x+3y2.
16. D: x2+y2=9, x2+y2=16, x=0, y=0 (x 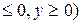 ;
;  =(2y-5x)/(x2+y2).
=(2y-5x)/(x2+y2).
17. D: x=1, y=0, y2=4x (y 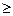 0);
0);  = 7x2+2y.
= 7x2+2y.
18. D: x2+y2=1, x2+y2=16, x=0, y=0 (x 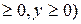 ;
;  =(x+3y)/(x2+y2).
=(x+3y)/(x2+y2).
19. D: x=2, y2=2x, y=0 (y 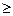 0);
0);  =7x2/4+y/2.
=7x2/4+y/2.
20. D: x2+y2=1, x2+y2=4, x=0, y=0 (x 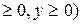 ;
;  =(x+2y)/(x2+y2).
=(x+2y)/(x2+y2).
21. D: x=2, y=0, y2=2x (y 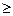 0);
0);  = 7x2/4+y.
= 7x2/4+y.
22. D: x2+y2=1, x2+y2=9, x=0, y=0 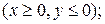
 =(2x-y)/(x2+y2).
=(2x-y)/(x2+y2).
23. D: x=2, y=0, y2=x/2 (y 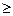 0);
0);  = 7x2/2+8y.
= 7x2/2+8y.
24. D: x2+y2=1, x2+y2=25, x=0, y=0 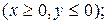
 =(x-4y)/(x2+y2).
=(x-4y)/(x2+y2).
25. D: x=1, y= 0, y2=4x (y  ;
;  = 6x+3y2.
= 6x+3y2.
26. D: x2+y2=4, x2+y2=16, x=0, y=0 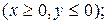
 =(3x-y)/(x2+y2).
=(3x-y)/(x2+y2).
27. D: x=2, y= 0, y2=x/2 (y  ;
;  = 4x+6y2.
= 4x+6y2.
28. D: x2+y2=4, x2+y2=9, x=0, y=0 (x 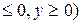 ;
;  =(y-4x)/(x2+y2).
=(y-4x)/(x2+y2).
29. D: x=1/2, y= 0, y2=2x (y  ;
;  = 4x+9y2.
= 4x+9y2.
30. D: x2+y2=4, x2+y2=9, x=0, y=0 (x 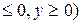 ;
;  =(y-2x)/(x2+y2).
=(y-2x)/(x2+y2).
Задание 5. Найти объем тела, заданного ограничивающими его поверхностями.
1. y=16 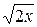 , y=
, y= 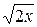 , z=0, x+z=2.
, z=0, x+z=2.
2. y=5 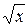 , y=5x/3, z=0, z=5+5
, y=5x/3, z=0, z=5+5 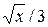 .
.
3. x2+y2=2, y= 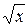 , y=0, z=0, z=15x.
, y=0, z=0, z=15x.
4. x+y=2, y= 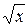 , z=12y, z=0.
, z=12y, z=0.
5. x=20 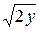 , x=5
, x=5 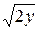 , z=0, z+y=1/2.
, z=0, z+y=1/2.
6. x=5 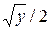 , x=5y/6, z=0, z=
, x=5y/6, z=0, z= 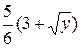 .
.
7. x2+y2=2, x= 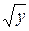 , x=0, z=0, z=30y.
, x=0, z=0, z=30y.
8. x+y=2, x= 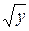 , z=12x/5, z=0.
, z=12x/5, z=0.
9. y=17 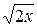 , y=2
, y=2 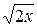 , z=0, x+z=1/2.
, z=0, x+z=1/2.
10. y=5 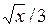 , y=5x/9, z=0, z=5(3+
, y=5x/9, z=0, z=5(3+ 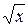 )/9.
)/9.
11. x2+y2=8, y= 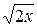 , y=0, z=0, z=15x/11.
, y=0, z=0, z=15x/11.
12. x+y=4, y= 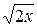 , z=3y, z=0.
, z=3y, z=0.
13. x= 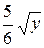 , x=
, x= 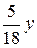 , z=0, z=
, z=0, z= 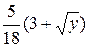 .
.
14. x=19 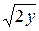 , x=4
, x=4 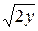 , z=0, z+y=2.
, z=0, z+y=2.
15. x2+y2=8, x= 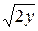 , x=0, z=30y/11, z=0.
, x=0, z=30y/11, z=0.
16. x+y=4, x= 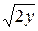 , z=3x/5, z=0.
, z=3x/5, z=0.
17. y=6 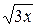 , y=
, y= 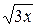 , z=0, x+z=3.
, z=0, x+z=3.
18. y= 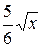 , y=
, y= 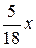 , z=0, z=
, z=0, z= 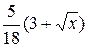 .
.
19. x2+y2=18, y= 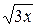 , y=0, z=0, z=5x/11.
, y=0, z=0, z=5x/11.
20. x+y=6, y= 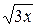 , z=4y, z=0.
, z=4y, z=0.
21. x=7 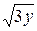 , x=2
, x=2 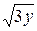 , z=0, z+y=3
, z=0, z+y=3
22. x=5 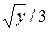 , x=5y/9, z=0, z=5(3+
, x=5y/9, z=0, z=5(3+ 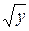 )/9.
)/9.
23. x2+y2=18, x= 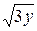 , x=0, z=0, z=10y/11.
, x=0, z=0, z=10y/11.
24. x+y=6, x= 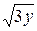 , z=4x/5, z=0.
, z=4x/5, z=0.
25. y= 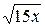 ,
, 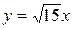 , z=0, z=
, z=0, z= 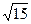 (1+
(1+ 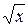 ).
).
26. x2+y2=50, y= 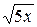 , y=0, z=0, z=3x/11.
, y=0, z=0, z=3x/11.
27. x+y=8, y= 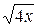 , z=3y, z=0.
, z=3y, z=0.
28. x=16 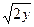 , x=
, x= 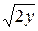 , z+y=2, z=0.
, z+y=2, z=0.
29. x=15 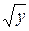 , x=15y, z=0, z=15(1+
, x=15y, z=0, z=15(1+ 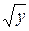 ).
).
30. x2+y2=50, x= 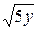 , x=0, z=0, z=6y/11.
, x=0, z=0, z=6y/11.
Задание 6. Вычислить тройной интеграл.
1.  x dx dy dz;
x dx dy dz;
V: y=10x, y=0, x=1, z=xy, z=0.
2. 
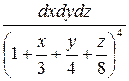 ;
;
V: 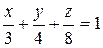 , x=0, y=0, z=0.
, x=0, y=0, z=0.
3.  15(y2+z2) dx dy dz;
15(y2+z2) dx dy dz;
V: z=x+y, x+y=1, x=0, y=0, z=0.
4.  (3x+4y) dx dy dz;
(3x+4y) dx dy dz;
V: y=x, y=0, x=1, z=5(x2+y2), z=0.
5.  (1+2x3) dx dy dz;
(1+2x3) dx dy dz;
V: y=9x, y=0, x=1, z= 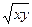 , z=0.
, z=0.
6.  (27+54y3) dx dy dz;
(27+54y3) dx dy dz;
V: y=x, y=0, x=1, z= 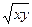 , z=0.
, z=0.
7.  y dx dy dz;
y dx dy dz;
V: y=15x, y=0, x=1, z=xy, z=0.
8. 
 ;
;
V: 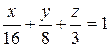 , x=0, y=0, z=0.
, x=0, y=0, z=0.
9.  (3x2+y2) dx dy dz;
(3x2+y2) dx dy dz;
V: z=10y, x+y=1, x=0, y=0, z=0.
10.  (15x+30z) dx dy dz;
(15x+30z) dx dy dz;
V: z=x2+3y2, z=0, y=x, y=0, x=1.
11.  (4+8z3) dx dy dz;
(4+8z3) dx dy dz;
V: y=x, y=0, x=1, z= 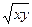 , z=0.
, z=0.
12.  (1+2x3) dx dy dz;
(1+2x3) dx dy dz;
V: y=36x, y=0, x=1, z= 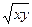 , z=0.
, z=0.
13.  21xz dx dy dz;
21xz dx dy dz;
V: y=x, y=0, x=2, z=xy, z=0.
14. 
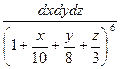 ;
;
V: x/10+y/8+z/3=1, x=0, y=0, z=0.
15.  (x2+3y2) dx dy dz;
(x2+3y2) dx dy dz;
V: z=10x, x+y=1, x=0, y=0, z=0.
16.  (60y+90z) dx dy dz;
(60y+90z) dx dy dz;
V: y=x, y=0, x=1, z=x2+y2, z=0.
17. 
 dx dy dz;
dx dy dz;
V: y=9x, y=0, x=1, z= 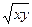 , z=0.
, z=0.
18.  (9+18z) dx dy dz;
(9+18z) dx dy dz;
V: y=4x, y=0, x=1, z= 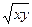 , z=0.
, z=0.
19.  3y2 dx dy dz;
3y2 dx dy dz;
V: y=2x, y=0, x=2, z=xy, z=0.
20. 
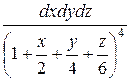 ;
;
V: x/2+y/4+z/6=1, x=0, y=0, z=0.
21.  x2 dx dy dz;
x2 dx dy dz;
V: z=10(x+3y), x+y=1, x=0, y=0, z=0.
22.  (8y+12z) dx dy dz;
(8y+12z) dx dy dz;
V: y=x, y=0, x=1, z=3x2+2y2, z=0.
23.  63(1+2
63(1+2 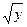 ) dx dy dz;
) dx dy dz;
V: y=x, y=0, x=1, z= 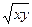 , z=0.
, z=0.
24.  (x+y) dx dy dz;
(x+y) dx dy dz;
V: y=x, y=0, x=1, z=30x2+60y2, z=0.
25. 
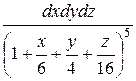 ;
;
V: x/6+y/4+z/16=1, x=0, y=0, z=0.
26.  xyz dx dy dz;
xyz dx dy dz;
V: y=x, y=0, x=2, z=xy, z=0.
27.  y2 dx dy dz;
y2 dx dy dz;
V: z=10(3x+y), x+y=1, x=0, y=0, z=0.
28. 
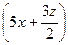 dx dy dz;
dx dy dz;
V: y=x, y=0, x=1, z=x2+15y2, z=0.
29.  (x2+4y2) dx dy dz;
(x2+4y2) dx dy dz;
V: z=20(2x+y), x+y=1, x=0, y=0, z=0.
30. 
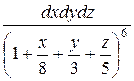 ;
;
V: x/8+y/3+z/5=1, x=0, y=0, z=0
Литература
1. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов. В 2 т. Т.1/ Н.С. Пискунов. – Изд. стер. – М.: Интеграл-Пресс, 2004. – 415 с.
2.Высшая математика в упражнениях и задачах. В 2 ч.: учеб. пособие для вузов. Ч. 2 / П.Е. Данко [и др.]. - 6-е изд. - М.: ОНИКС: Мир и Образование, 2006. - 304 с.
3. Задачи и упражнения по математическому анализу для втузов: [учеб. пособие для втузов] / Г.С. Бараненков [и др.]; под ред. Б.П. Демидовича. – М.; Владимир: Астрель: Изд-во АСТ: ВКТ, 2008. - 495 с.
Содержание
Введение. 4
1. Двойной интеграл. 5
1.1 Определение и основные свойства двойного интеграла. 5
1.2. Вычисление двойного интеграла. 6
1.3. Замена переменных в двойном интеграле. 6
2. Тройной интеграл. 7
2.1. Определение и свойства тройного интеграла. 7
2.2 Замена переменных в тройном интеграле. 8
Пример выполнения расчетно-графической работы.. 9
Варианты расчетно-графической работы.. 13
Литература. 22
Содержание. 23
Составители: Камозина О.В.
Козлова О.Н.
Кратные интегралы
Методические указания и задания к расчетно-графической работе для студентов всех направлений подготовки бакалавров
очной формы обучения
Формат Объем Тираж Заказ
Брянск, Станке Димитрова 3, Редакционно-издательский отдел
Отпечатано: Печатный цех БГИТА






