Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Владимирский государственный университет
имени Александра Григорьевича и Николая Григорьевича Столетовых"
(ВлГУ)
дисциплина «Теория и системы управления»
Лабораторная работа №3
(Обучающая)
Исследование систем автоматического управления техническими объектами
Владимир 2012
Исходные данные

Рис. 1. Схема САУ
Выбрать структуру и рассчитать параметры последовательно-параллельного КУ
Варианты заданий
| № | Неизменяемая часть системы | Требования к синтезируемой системе | ||||
| sзад, % |  , с , с
| 
| 
| 
| ||
 , , 
| 1,5 | 
| 
| |||
| - | 1,2 | 
| 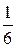
| |||
| - | 1,3 | 
| 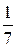
| |||
| - | 1,5 | 
| 
| |||
| - | 1,6 | 0,1 | 
| 
| ||
| - | 1,8 | 0,3 | 
| 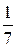
| ||
| - | 1,4 | 0,2 | 
| 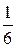
| ||
| - | 1,7 | 
| 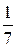
| |||
| - | 0,2 | 
| 
| |||
| - | 1,9 | 0,5 | 
| 
| ||
| - | 2,2 | 0,4 | 
| 
|
Цели работы:
1. Определение передаточных функций разомкнутой и замкнутой систем, по задающему и возмущающему воздействиям
2. Построение модели исследуемой САУ, используя Matlab(Simulink)
3. Оценка устойчивости замкнутой нескорректированной системы регулирования по критерию Гурвица
4. Оценка устойчивости замкнутой системы по критерию Михайлова
5. Оценка устойчивости замкнутой системы по критерию Найквиста
6. Оценка запаса устойчивости замкнутой системы
по АФХ разомкнутой системы
Пример.
- Определение передаточных функций разомкнутой и замкнутой систем, по задающему и возмущающему воздействиям
Передаточная функция первого звена:

Передаточная функция второго звена:W2= 
Передаточная функция разомкнутой системы
WP=W1*W2= 
Передаточная функция замкнутой системы:


Передаточная функция замкнутой системы по задающему воздействию:
ε(t)=y(t)-x(t)
x(t)=y(t)*W1*W2 => y(t)=x(t)/(W1*W2);
ε(t)=x(t)*(1/(W1*W2*W3)-1)=x(t)*(1-WP)/WP;

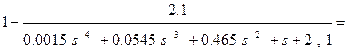

Передаточная функция замкнутой системы по возмущающему воздействию:
ε(t)=f(t)-x(t)*W1;
x(t)=f(t)*W2=> f(t)=x(t)/W2;
ε(t)=x(t)*(1/W3-W1*W2);
WP=W2
Ф(p)= 
Фεg=0= 
- Построение модели исследуемой САУ, используя Matlab (Simulink)
Строим в Simulink модель исследуемой САУ:

Рис. 2. Модель нескорректированной исследуемой САУ
(Построение переходной характеристики):
Рис. 3. Переходная характеристика нескорректированной исследуемой САУ
Из рисунка 3 видно, что исследуемая САУ устойчива.Определим показатели качества.

где 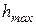 -максимальное значение переходной характеристики замкнутой САУ
-максимальное значение переходной характеристики замкнутой САУ 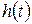 ;
;
 - установившееся значение
- установившееся значение 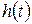 .
.
σ=(1.3-1)/1*100=30%
Время регулирования tрег - минимальная величина, при которой удовлетворяется условие:
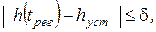
где  - заданная величина ошибки (обычно
- заданная величина ошибки (обычно  =0,05
=0,05  ).
).
 h (t)
h (t)

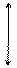

 2 δ
2 δ






 hуст
hуст
hmax

 t
t
 tрег
tрег
Рис. 4. График переходного процесса САУ
 =0,05
=0,05  =0.05
=0.05

tрег=4,5с.
Показатели качества, время регулирования tрег не удовлетворяет заданным в условии  = 1.5с
= 1.5с
- Оценка устойчивость замкнутой нескорректированной системы регулирования по критерию Гурвица
Этот критерий позволяет сказать, где находятся корни характеристического уравнения, не решая его. Их коэффициентов характеристического уравнения  , составляют сначала главный определитель Гурвица следующим образом:
, составляют сначала главный определитель Гурвица следующим образом:
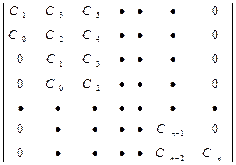
Характеристическое уравнение для моей САУ имеет следующий вид:
0,0015s4+0.0545s3+0.465s2+s+2.1=0
Для устойчивости системы необходимо и достаточно чтобы все диагональные миноры данного определителя были >0.
Составим определитель Гурвица.


(Сделать вывод): САУ по критерию Гурвица – устойчива (или нет?), так как все диагональные миноры положительны – да или нет?
- Оценка устойчивость замкнутой системы по критерию Михайлова
Характеристическое уравнение замкнутой системы

Составим характеристическое уравнение передаточной функции замкнутой САУ.
D(s)=0.0015s4+0.0545s3+0.465s2+s+2.1
САУ устойчива, если при изменении частоты w от 0 до +∞,начав движение из точки, лежащей на положительной вещественной полуоси, вращаясь против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов, повернувшись угол n*(π/2), где n – степень характеристического уравнения.
В системе Matlab построим годограф Михайлова.
Текст программы
num=[0.0015 0.0545 0.465 1 2.1];
den=[1];
w=0.0001:0.01:10;
apk=freqs(num,den,w);
u=real(apk);
v=imag(apk);
plot(u,v);grid
(Построение графика годографа Михаилова)
Рис. 5.Годограф Мехайлова
Видно, что система (устойчива или нет?),так как при изменении частоты w от 0 до +∞,начав движение из точки, лежащей на положительной вещественной полуоси, вращаясь против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов, повернувшись угол 4*(π/2).
Оценка устойчивость замкнутой системы по критерию Найквиста
Устойчивость замкнутой системы определяем по АФХ разомкнутой. Сначала определим устойчивость разомкнутой системы по критерию Гурвица. Определим характеристическое уравнение разомкнутой системы:
D(s)= 0.0015s4+0.0545s3+0.465s2+s
Составим определитель Гурвица.


Так как последний определитель равен 0, то разомкнутая система находиться на границе устойчивости, и при построении графика его необходимо дополнить дугой до положительной вещественной полуоси.И для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала точку с координатами (-1;j0).
Характеристическое уравнение разомкнутой системы

Текст программы:
num=[2.1];
den=[0.0015 0.0545 0.465 1 0];
w=1:0.1:30;
APK=freqs(num,den,w)
u=real(APK);
v=imag(APK);t=0:pi/100:2*pi;
x=sin(t);
y=cos(t);
plot(u,v,x,y);grid
(Построение АФХ замкнутой системы)
Рис. 6. АФХ замкнутой системы
Замкнутая система устойчивая (или нет?) т.к. разомкнутая система не охватывает точку -1,j0
- Оценка запаса устойчивости замкнутой системы по АФХ разомкнутой системы
На рисунке 6 показаны запасы устойчивости по фазе и модулю
Текст программы:
num=[2.1];
den=[0.0015 0.0545 0.465 1 0];
w=1:0.1:30;
APK=freqs(num,den,w)
u=real(APK);
v=imag(APK);t=0:pi/100:2*pi;
x=sin(t);
y=cos(t);
plot(u,v,x,y);grid
(Построение АФХ разомкнутой системы)
Рис. 7. АФХ разомкнутой системы
Из рисунка 6 видно, что есть запас (или нет?) устойчивости по фазе и амплитуде. Система устойчива (или нет?).
Показатели качества tрег не удовлетворяют заданным в условии.
Следует синтезировать корректирующее устройство, обеспечивающее заданные показатели качества работы системы.
Заключение
В данной работе было проведено исследование системы углом, в ходе которого были синтезированы корректирующие устройства для достижения требуемых показателей качества.
Список использованной литературы
1. Методические указания к курсовой работе по дисциплине "Теория управления" для студентов специальности 210100 - "Управление и информатика в технических системах" Уфимск. гос. авиац. техн. ун-т; Сост. Б.Г. Ильясов, Л.А. Болотовская. Уфа, 1998.- 24 с.
2. Теория автоматического управления: Учеб. для вузов по спец. "Автоматика и телемеханика", в 2-х ч. 4.1 Теория линейных систем автоматического управления/Н.А.Бабаков, А.А.Воронов, А.А.Воронова и др. Под ред. А.А.Воронова - 2-е изд.перераб. и доп. - М.: Высшая школа, 1986. - 367 с.
3. Бесекерский В.А., Попов Б.П. Теория систем автоматического управления. - М. Наука, 1976. - 605 с.






