Увеличиваем коэффициент K на 20% с K = 5 до K = 6
Переходная функция Импульсная переходная функция
Увеличиваем коэффициент T на 100% с T = 0,5 до T = 1
Переходная функция Импульсная переходная функция
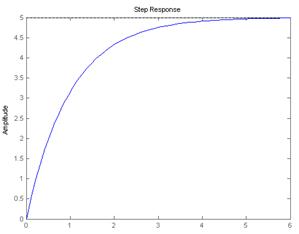
Вывод: -при увеличении коэффициента усиления K на 20%, амплитуды переходной и импульсной переходной функций также возрастают на 20% (с 5 до 6 для переходной функции и с 10 до 12 для импульсной переходной функции);
при увеличении постоянной времени T на 100%, время переходного процесса увеличивается на 100% с 3 сек. до 6 сек.
Апериодическое звено второго порядка
Передаточная функция звена имеет вид
Часто используют описание звена в виде:
Т.к. все корни вещественные то следует,что 
.
где 
- коэффициент затухания.
Определяем переходную функцию звена:
Строим временные характеристики: переходную функцию и импульсную переходную функцию….
Уменьшаем коэффициент K на 25% с K = 4 до K = 3
Строим временные характеристики: переходную функцию и импульсную переходную функцию….
Уменьшаем постоянную времени T на 20% с T = 0,5 до T = 0,4
Строим временные характеристики: переходную функцию и импульсную переходную функцию….
Увеличиваем коэффициент затухания на 25% с 
= 1,6 до = 2
Строим временные характеристики: переходную функцию и импульсную переходную функцию….
Вывод: - при уменьшении коэффициента усиления K на 25% до K = 3 амплитуда переходной и импульсной переходной функций также уменьшается на 25% (с 4 до 3 у переходной функции и с 2,1 до 1,575 у импульсной переходной функции);
- при уменьшении постоянной времени на 20% до T = 0,4 время переходного процесса также уменьшается на 20 % с 9 сек. до 7,2 сек.;
- при увеличении коэффициента затухания на 25% до = 2 время переходного процесса возрастает на 100% с 7 сек. до 14 сек.
Колебательное звено второго порядка
Передаточная функция звена имеет вид
Часто используют описание колебательного звена в виде:
т.е. 
.
Определяем переходную функцию звена:
Производим исследования: см. пример выше.
Интегрирующее звено
Передаточная функция звена имеет вид
Определяем переходную функцию звена:
Производим исследования: см. пример выше.
Изодромное звено
Это звено имеет передаточную функцию
т.е. его можно представить как параллельное соединение интегрирующего и пропорционального (безынерционного) звеньев. После простых преобразований это звено можно также записать в виде:
(2)
где (1+T s) - форсирующее звено, T= K 2/ K 1, K=K1.
Таким образом, в соответствии с (2) изодромное звено может быть также представлено как последовательное соединение интегрирующего и форсирующего звеньев.
Т.е. передаточная функция звена которая реализуется в Matlab:
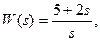
Временные характеристики
Определяем переходную функцию звена:
Производим исследования: см. пример выше.
