Профиль – вертикальный разрез вдоль заданного направления линий. По горизонтальной линии при построении профиля задают значение горизонтальных проложений обычно в масштабе карты или плана, а по вертикальной линии задают значения высот точек пересечения линий с горизонталями и точек перегиба профиля. Обычно вертикальный масштаб делают крупнее в 10 раз
Уклоном линии местности i называют отношение превышения между точками h, к горизонтальному проложению между ними S: i=h/S * 1000.
Уклон линии в зависимости от знака превышения может быть положительным или отрицательным.
Заложение а - кратчайшее расстояние (на плане) между двумя точками смежных горизонталей. Между заложением и углом наклона склона v следующая зависимость tg v = h / a, где а- заложение, h – высота сечения рельефа.
Чем больше заложение, тем больше угол наклона, т.е. круче склон и наоборот. При углах наклона склона более 45 градусов горизонталями склон изобразить невозможно, поэтому такие элементы рельефа показывают условными знаками (обрыва, осыпи, скалы). Кроме этого условными знаками показывают мелкие элементы рельефа ямы, курганы, насыпи, карьеры. Естественно созданные формы рельефа показывают коричневым цветом, искусственно созданные черным.
17. Общие понятия о геодезических сетях.
Положение объектов земной поверхности описываются в геод. системе координат. Физическими носителями системы координат являются пункты геодезических сетей.
Геодезическая сеть – система пунктов на земной поверхности, закрепленных на местности специальными знаками и центрами, положение которых определено в плановом отношении (координаты х,у) и по высоте (h).
Государственная геодезическая сеть (ГГС) предназначена для решения задач:
1.для создания и распространения геодезической системы координат единой на всей территории страны.
2.для геодезического обеспечения картографирования страны и акваторий окружающих ее морей.
3.для геодезического обеспечения изучения земельных ресурсов в том числе и для кадастрового учета.
4.для изучения геодинамических явлений и гравитационного поля земли.
5.для обеспечения исходными геодезическими данными средств морской и аэрокосмической навигаций, аэрокосмического мониторинга земель.
Геодезические сети: 1.плановые, 2.высотные.
Пункты плановых сетей имеют координаты х,у, а высотных – высоты h.
Геодезический пункт состоит из знака и центра. Существуют различные виды центров, выбор конкретного вида центра зависит от его назначения, времени использования и требований к точности определения координат. Например, для закрепления пунктов сетей сгущения применяют центр, который состоит из бетонных монолитов, отвечающих за долговременность и сохранность вмонтированной в верхнем торце металлической марки. Отмеченная на марке точка является носителем координат. Над центрами располагаются геодезические знаки в виде пирамид высотой от 3 до 8 м.
18. Способы построения плановых геодезических сетей.
Современная ГГС включает в себя геодезические построения различных классов точности:
1.фундаментальная астрономо-геодезическая сеть.(ФАГС)(129 пунктов)
2.высокоточная геодезическая сеть (ВГС)
3.спутниковая геодезическая сеть I класса (СГС)
4.астрономо геодезическая сеть и государственные сети сгущения (АГС и ГСС)
5съемочная сеть (СС)
Методы построения ГГС:
Разработка и применение спутниковых методов для определения координат пунктов ГГС в настоящее время является приоритетным по сравнению с другими методами. В тоже время они имеют ряд ограничений затрудняющих их условия на застроенных территориях, залесенных местностях и др.
Триангуляция – построение цепочки треугольников, смежно расположенных, в каждом из которых измеряют все углы, а так же длину базисных сторон в начале и конце цепочки. Имеется возможность уравнивания измеренных углов и передача координат на вершины треугольников.
Полигонометрия – метод определения координат заключающийся в проложении полигонометрического хода, в котором измеряются длины линий и углы поворота между сторонами хода
19. Создание планового геодезического обоснования теодолитной съемки проложением теодолитных ходов.(классификация теодолитных ходов, рекогносцировка, измерение углов и линий)
Теодолитная съемка предусматривает съемку только контуров без отображения рельефа. При съемке обязательному отображению на планах и картах подлежат все объекты местности, выражающиеся в масштабе этих планов и карт, а так же объекты невыраженные в масштабе, но предусмотренные действующими условными знаками.
Классификация теодолитных ходов
1.разомкнутый т.х – ход. Который опирается на две точки с известными координатами. Самый надежный, т.к имеется контроль измеренных величин и исходных данных.
2.замкнутый т.х (полигонный) сомкнутый многогугольник, обычно привязанный к одному из пунктов геодезическогообоснования. В этом случае имеется контроль измеренных величин, но отсутствует контроль исходных данных.
3.висячий т.х. используется редко, т.к нет контроля исходных данных и вычислений.
20. привязка теодолитного полигона к геодезической сети.
Для того чтобы определить координаты начальной точки полигона и дирекционного угла начальной стороны решают задачу привязки теодолитного полигона к пунктам геодезической сети (точки А и В). Координаты пунктов А и В известны поэтому решив обратную геодезическую задачу определим дирекционный угол 
.
В поле измеряют горизонтальные углы между направление АВ и В1, левый 
и правый 
, которые в сумме должны быть 
. Эти углы называются примычными. Так же необходимо измерить горизонтальные углы 
и 
на точке 1. Между стороной В1 и стороной хода 12 
Для вычисления горизонтального проложения между точками В и 1 измеряют длину линии (D) и угла наклона (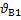
) 
.
Алгоритм вычисления:
1.вычисление дирекционного угла направления В1: 
. Контроль: 
2.вычисление дирекционного угла направления 12: 
. Контроль: 
3.вычисление начальной точки полигона. Решаем прямую геодезическую задачу.
, 
21.Уравнивание замкнутого теодолитного хода (последовательность, формулы, допуски)
Замкнутый т.х.(полигон)-имеет контроль измеренных величин, отсутствует контроль исходных данных.
Исходным теод-ым ходом яв-ся координаты одной из его точек, наз-ой начальной и дирекционный угол одной из сторон.При произ-ве работ стремятся совместить одну из точек этой стороны с начальной точкой теодолитного полигона. Для того, чтобы определить координаты нач-ой точки (х1,у1)и дирекциооный угол нач-ой стороны (α1,2), решают задчу привязки теод-го хода полигона к пунктам геод-ой сети. (точки А и В). Координаты пунктов А и В известны, поэтому реши обратную задачу опред-ют дирекционный угол α1,2 (выч-ие гор-го проложения Sав необходимо лишь для контроля). В поле измеряют гор-ые углы м/у направлением АВ и В1, левый λв и правый βв, кот-ые в сумме должны составлять 3600. Эти углы наз-ют примычными. Также необходимо измерить гор-ые углыλ1 и β1 на точке между стороной В1 и стороной хода 1-2, также с контролем: λ1+ β1=3600. Для выч-ия гор-го проложения между точками В и 1 измеряют длину динии (D) и угол наклона: S=D*cosγ.
Алгоритм вычисления:
1) Выч-ют дир-ый угол направления В1- λ1. λ1В= λАВ+1800- βВ. Для контроля выч-ют: λ1В=λАВ-1800
Выч-ия значения дерек-го угла должны сходиться до 1,5 минут (в пределах). Если суммы поворота измерены в точности с 30сек.
2)Выч-ие дир-го угла направления 1-2. λ12= λВ1+1800- β1. Контроль:. λ12= λВ1+λ1-1800. Расхождение не должно быть больше 1,5 минуты. За значение берем среднее.
3)Выч-ие координат начальной точки. Решаем прямую геод-ую задачу: Х1=ХВ+SВ1*cosαВ,1. У1=УВ+SВ1*sinαВ,1.
Схема замкнутого и диагонального теодолитных ходов
Внутри замкнутого хода можно проложить диагональный ход, опирающийся на вершины основного хода (на рис. 1.16 ход 6-8-9-2).
В разомкнутом (рис. 1.14) и замкнутом (рис. 1.16) теодолитных ходах кроме необходимых для определения координат точек хода измерений выполнены избыточные измерения: в разомкнутом ходе избыточными являются примычные углы βn, β'n; угол βn-1 и сторона dn, а в замкнутом — углы β6, β7 и d7, что позволяет выполнить уравнивание и оценку точности этих ходов.
Известно, что каждое избыточное измерение приводит к условному уравнению, в рассматриваемом случае имеем три избыточных измерения, которые дают одно условное уравнение фигуры и условные уравнения абсцисс и ординат.
В теодолитном ходе угловая невязка (свободный член условия фигур)
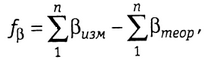(1.12)
где 
- сумма измеренных в теодолитном ходе углов, а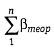 
- их теоретическая сумма. В замкнутом теодолитном ходе с n измеренными углами, как известно из геометрии
(1.13)
следовательно, в замкнутом теодолитном ходе
(1.13)
В разомкнутом теодолитном ходе теоретическая сумма углов зависит от расположения исходных сторон, и поэтому целесообразно разомкнутый ход превратить в замкнутый путем продолжения опорных линий до их пересечения и использовать его для определения .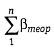
На рисунке 1.14 для измеренных левых углов имеем
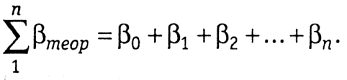
В полученном замкнутом полигоне сумма углов
где n — число измеренных углов. Из этого выражения находим
т. е. в рассматриваемом случае, учитывая
получаем
На рисунке 1.17
22.Уравнивание разомкнутого теодолитного хода (последовательность, формулы, допуски)
Разомкнутых т.х.- опирается на 2 точки с известными координатами. Яв-ся самым надежным т.к.имеется контроль измеренных величин и исходных данных.
Схема разомкнутого теодолитного хода
Формулы (1.7) решают прямую геодезическую задачу на плоскости, в которой при известных прямоугольных координатах хH,уH, горизонтальном проложении d и дирекционном угле а требуется определить координаты х1, у1, точки 1.
В обратной задаче по известным координатам х1,у1; х2,у2, точек 1 и 2 (рис. 1.15) требуется определить дирекционный угол α и горизонтальное проложение d.
Рис.1.15 Решение обратной задачи на плоскости
На рисунке 1.15 из прямоугольного треугольника 122'
(1.8)
откуда находят дирекционный угол α. Горизонтальное проложение
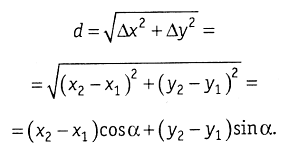(1.9)
Измерив горизонтальный угол β0 между исходной и определяемой сторонами, на pисунке 1.14 имеем
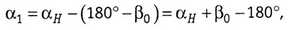(1.10)
если измерены левые по направлению теодолитного хода углы.
Если измерены правые углы β'0' β'1 и т.д., то, учитывая β0 = 360° - β'0, вместо формулы (1.10) находим
(1.11)
Следовательно, для определения координат точек теодолитного хода необходимо начинать ход с опорной точки, имеющей координаты хH,уH, и в этой начальной опорной точке измерить примычный угол β0 и β'0 между линией с известным дирекционным углом и линией d1 хода.
