11.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано. Плоские прямоугольные координаты (в дальнейшем координаты) 1 (х1, у1) начальной точки линии 12, дирекционный угол α12, горизонтальное проложениеs12 (рис. 4.1). Требуется вычислить координаты конечной точки 2 (х2, у2) этой линии.
Решение. Вначале дадим определение понятию «приращение координат». Направленный прямолинейный отрезок 12 можно считать вектором, длина которого равна s12. Приращение координат - ортогональная проекция вектора на координатные оси прямоугольной системы координат. Из математики известно, что проекция вектора на координатную ось равна координате его конца без координаты начала. Поэтому приращения координат
∆x12=x2 – x1, ∆y12 = y2 – y1 (4.1)
Напомним, что длина вектора равна корню квадратному из суммы квадратов его проекций на оси координат, т. е.
Поскольку направление вектора может изменяться от 0 до 2 π, то приращения координат могут быть как положительными, так и отрицательными величинами в зависимости от значения дирекционного угла α12. Приращения координат в системе координат хОу будут (рис. 4.1): ∆х12>0,∆y12>0. Из решения прямоугольного треугольника 1А2 (см. рис. 4.1) находят
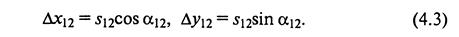
Искомые координаты точки 2, как следует из формулы (4.1), будут
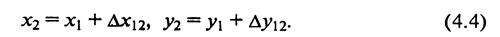
Задача. Дано: х1 = +250,15 м; y1 = - 410,34 м; α12 = 134º10, 0’; s= 150,24 м. Вычислить х2 и у2.
Решение. По формулам (4.3) получим: ∆x12= - 104,68 м; ∆y12 = +107,77 м. Неизвестные координаты вычисляют по формуле (4.4). Они равны: х2 = +250,15 + (- 104,68) = 145,47 м;
у2 = -410 34+ 107,77 = -302,57 м.
Решение прямой геодезической задачи тождественно решению задачи по определению координат точки способом полярных координат, когда сделан перенос начала координат из точки О в точку 1.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано. Координаты точек 1(х1, у1) и 2(х2, у2) концов линии 12. Требуется вычислить дирекционный угол направления 12 – α12 и горизонтальноепроложение s12.
Решение. Из прямоугольного треугольника (см. рис. 4.1) следует, что искомый дирекционный угол можно найти из следующих соотношений:
Для контроля решения обратной геодезической задачи горизонтального проложения применяют также формулу
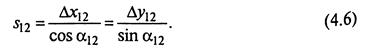
Чтобы однозначно определить числовое значение дирекционного угла α12, необходимо принять во внимание знаки приращений координат, которые определяют направление линии.
Алгоритм для нахождения дирекционного угла линии 12 из решения обратной геодезической задачи имеет вид
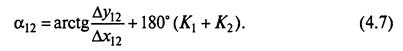
При этом, если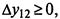 
то К1=0; иначе К1=1. Если 
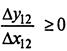, то К2=0; иначе К2=1.
Задача. Даны координаты двух точек, м: 1 (+123,37, - 245,23), 2 (-256,23; +300,18). Найти дирекционный угол α21 и горизонтальноепроложениеs21.
Pешение. Вначале вычисляют приращения координат. Получают:
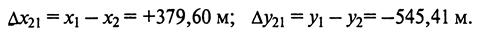
По формуле (4.7) находят дирекционный угол направления 21:
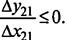
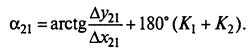
В примеру: ∆y12<0, поэтому K1=1,При таком значении неравенства К2=1. Окончательно запишем: α21= -55º09’45’’ + 180º(1+1) = =304º50’15’’
Горизонтальное положение
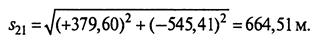
Вычисления контролируют по одной из формул (4.6):
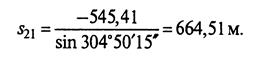
Значение дирекционного угла можно также определить по названию румба линии. Для этого находят угловое значение румба линии 21, используя модули приращений координат
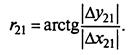
B примере знаки приращений координат имеют следующие значения: ∆х21>0,∆y21<0. Поэтому линия 21 имеет северо-западное направление. Тогда r21=C3:55º09'45". Дирекционный угол (см. рис. 3.12):
α21=360º - 55º09'45"=304º50’15’’.
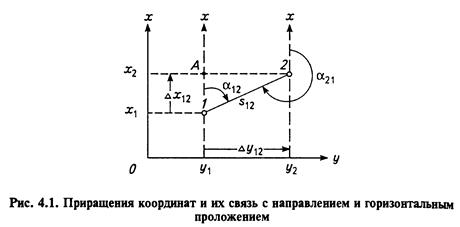
В таблице приведен пример решения обратной геодезической задачи в программной среде Excel. Для определения дирекционного угла α21, выраженного в градусах, применен алгоритм (4.7) В качестве исходных данных использованы координаты х1, у1 и х2, у2двух конечных точек линии 12. Там же приведено решение прямойгеодезическойзадачи.
