Использование сети Файстеля

Лабораторная работа № 1

 

Битовые операции. Гаммирование.

 

Задание: Ознакомиться (повторить) с основными операциями битовой арифметики и наложением масок. Ознакомиться с понятием шифра гаммирования.

 

Время выполнения: 1 пара.

 

Шифрование методом гаммирования – это метод "наложения" ключевой последовательности – гаммы – на открытый текст. "Наложение" заключается в позначном (побуквенном) сложении или вычитании по тому или иному модулю. В силу простоты своей технической реализации и высоких криптографических качеств эти шифры получили широкое распространение.

Исторически первый шифр гаммирования совпадал, по сути, с шифром Виженера, однако без использования самой таблицы Виженера. Заметим, что таблица Виженера представляет собой квадрат, каждая строка и каждый столбец которого – некоторая перестановка знаков данного алфавита. Произвольная такая таблица называется латинским квадратом, а алгоритм, основанный на использовании такой таблицы, называется алгоритмом табличного гаммирования.

В современной компьютерной криптографии алфавитом языка являются возможные значения битов (т.е. 0 и 1), а таблица гаммирования имеет следующий вид:

Т. обр., компьютерное гаммирование есть наложение псевдослучайной битовой последовательности (гаммы) на исходный текст с помощью операции XOR (или сложение по модулю 2, что одно и то же).

В связи с тем, что такое гаммирование требует работы с каждым отдельным битом исходного текста и гаммы, необходимо более подробно рассмотреть отдельные операции манипуляции с битами чисел.

При работе с битами чаще всего используют следующие операции: И (and), ИЛИ (or), Исключающее ИЛИ (xor) и НЕ (not). В зависимости от значений операндов значения этих операций следующие:

A, B	A and B	A or B	A xor B	not A
0, 0
0, 1
1, 0
1, 1

При манипуляции выделяют также операцию наложения битовой маски. Это такая операция, которая не меняет значения битов своего операнда, находящихся на некоторых выбранных позициях, а все остальные биты обнуляет. Например, операция маскирования битов 3 и 4 (начиная с 0) числа 127 (01111111) возвращает число 24 (00011000). Эта операция обычно используется для определения значения определенных бит числа.

Маскирование выполняется так: составляется число-маска той же битовой длины, как и у операнда этой операции. Затем те его биты, которые требуется оставить у операнда неизменными, устанавливаются в 1, а остальные устанавливаются в 0. Операция наложения маски состоит в вычислении побитовой конъюнкции (операции and) битов маски с соответствующими битами операнда.

В примере выше для того, чтобы определить 3-й и 4-й биты числа, составляется число-маска, у которого 3-й и 4-й биты равны 1, а остальные равны 0. В битовой записи такое число имеет вид: 00011000. Операция наложения маски имеет вид:

Т.к. большинство языков не поддерживает запись числа в двоичной системе счисления, то маску необходимо представлять в десятичном виде: 00011000₂ = 24₁₀.

Т.обр., операция наложения маски mask на число x имеет вид:

y:= mask and x;

где у – результат операции.

 

При выполнении работы требуется решить следующие задачи:

1. Создать функцию, принимающую от пользователя число x типа longint (32-битное целое число), и возвращающую значение его бита, находящегося на позиции pos. Номер этого бита pos должен быть одним из аргументов этой функции. Нумерацию битов начинать с нуля.

Для выполнения этого задания необходимо сделать следующее:

· Произвести правый сдвиг (shr) числа x на pos позиций.

· С помощью наложения маски определить значение нулевого бита получившегося числа.

Напомним, что если нас интересуют определенные биты числа, то мы должны составить маску, биты в которой равны 1, несли они стоят на том же месте, что и интересующие нас биты у числа, и 0 в противном случае.

2. Модифицировать предыдущую функцию. Новая функция должна вернуть значение числа, составленного из len бит числа x, начинающихся с позиции pos (другими словами, она должна вернуть число, составленное из бит с номерами pos, pos+1, …, pos+len-1 числа х). Решение этой задачи полностью аналогично решению предыдущей задачи, за исключением маски.

Подсказка: в этом случае маска равна числу 2^len-1.

3. Создать функцию, выполняющую гаммирование некоторой битовой последовательности («открытого текста»). Эта последовательность должна быть задана в виде массива целых чисел. При этом предполагается следующее:

a. Открытый текст должен представлять собой массив целых чисел любой размерности. Его можно задать вручную или сгенерировать произвольно.

b. Гамма должна представлять собой генерируемую программой последовательность ПСЧ (псевдослучайных чисел). Ключом (секретной компонентой) шифра должно быть начальное значение генератора ПСЧ. Т. обр., при работе программы необходимо присвоить переменной RandSeed значение, а затем его сохранить в тайне.

c. Шифротекст должен быть записан в массиве такой же длины, что и исходный текст. Массив должен быть составлен из чисел такой же размерности.

d. Получение шифротекста выполняется с помощью операции побитового xor члена массива, в который записан исходный текст, с соответствующим членом последовательности ПСЧ (т.е. с результатом вызова функции random()).

4. Создать функцию, выполняющую расшифрование битовой последовательности, зашифрованной с помощью функции, полученной на предыдущем шаге. Функция будет работать полностью аналогично функции 3, но ей обязательно передать то же значение RandSeed, которое использовалось при зашифровании текста.

 

Отчет по работе должен включать:

1. 2-минутное сообщение

2. программу-тест

 

 

 

Лабораторная работа № 2

 

Шифры перестановок. Понятие P-блоков.

 

Задание: Ознакомиться с понятиями перестановок, шифров перестановок и P-блоков.

 

Время выполнения: 1 пара.

 

Шифрами перестановки (ШП) называются такие шифры, преобразования из которых приводят к изменению только порядка следования символов исходного сообщения (но при этом не изменяются сами символы). Примером преобразования, которое может содержаться в шифре перестановки, является следующее правило. Каждая буква исходного сообщения, стоящая в тексте на позиции с четным номером, меняется местами с предшествующей ей буквой. В этом случае ясно, что и исходное, и шифрованное сообщение состоят из одних и тех же букв.

Широкое распространение получили шифры перестановки, использующие некоторую геометрическую фигуру. Преобразования из этого шифра состоят в том, что в фигуру исходный текст вписывается по ходу одного "маршрута", а затем по ходу другого выписывается с нее. Такой шифр называют маршрутной перестановкой. Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут: по горизонтали, начиная с левого верхнего угла поочередно слева направо и справа налево. Выписывать же сообщение будем по другому маршруту: по вертикали, начиная с верхнего правого угла и двигаясь поочередно сверху вниз и снизу вверх.

Пример. Зашифруем указанным способом фразу:

ПРИМЕРМАРШРУТНОЙПЕРЕСТАНОВКИ

используя прямоугольник размера 4´7:

П	Р	И	М	Е	Р	М
Н	Т	У	Р	Ш	Р	А
О	Й	П	Е	Р	Е	С
И	К	В	О	Н	А	Т

Зашифрованная фраза выглядит так:

МАСТАЕРРЕШРНОЕРМИУПВКЙТРПНОИ

Теоретически маршруты могут быть значительно более изощренными, однако запутанность маршрутов усложняет использование таких шифров.

Теоретически перестановкой называют любое биективное (т.е. взаимно однозначное) отображение некоторого конечного множества на само себя. Т.к. множество конечное, то все его элементы можно занумеровать, и перестановкой можно считать способ взаимно однозначного сопоставления последовательности чисел 1, …, n на себя. Для удобства перестановку можно представить в виде таблицы

		…	n-1	n
f(1)	f(2)	…	f(n-1)	f(n)

Пример перестановки из 4-х элементов:

Если по такому закону менять биты в каждой 4-ке бит исходного текста, то мы получим шифр перестановки. Такое преобразование само по себе является очень нестойким ко взлому, поэтому оно используется в качестве составляющей части многих алгоритмов. В этом случае оно называется блоком перестановки (или P-блоком, англ. P-box). Подробнее с P-блоками мы ознакомимся на лекции по теме «SP-сети».

Для того, чтобы расшифровать сообщение, зашифрованное по такому алгоритму перестановки, необходимо предложить обратную перестановку. Действительно, т.к. перестановка является взаимно однозначным отображением множества на себя, то для нее (как и для любого взаимно однозначного отображения) должно существовать обратное отображение. Проще говоря, обратное отображение поможет вернуть переставленные биты на свои места.

Для того, чтобы найти обратную перестановку к перестановке, заданной в табличном виде, нужно просто поменять строки этой таблицы местами. Например, к перестановке

обратная будет иметь вид:

или, переупорядочив столбцы по значению аргументов, получим

 

При выполнении работы требуется решить следующие задачи:

1. Реализовать программу, выполняющую шифрование исходного текста методом маршрутной перестановки. Для маршрутной перестановки используйте таблицу размера 5х6. Реализуйте также программу, выполняющую расшифрование зашифрованного текста. Для простоты и защиты от ошибок, пусть ваш текст содержит количество букв, кратное 30.

2. Реализовать процедуру, реализующей преобразование исходного текста с помощью 4-элементных перестановок. Для разбиения текста на 4-битные блоки можно использовать операции сдвигов и маскирование.

3. Реализовать процедуру, выполняющую расшифрование текста, зашифрованного с помощью процедуры, полученной на 2 шаге.

Отчет по работе должен включать:

1. 2-минутное сообщение

2. программу-тест

 

 

Лабораторная работа № 3

 

Шифры замены. S-блоки.

 

Задание: Ознакомиться с шифрами замены и S-блоками

 

Время выполнения: 1 пара.

 

Наиболее известными и часто используемыми шифрами являются шифры замены. Шифрами замены называются такие шифры, преобразования из которых приводят к замене каждого символа открытого сообщения на другие символы – шифробозначения, причем порядок следования шифробозначений совпадает с порядком следования соответствующих им символов открытого сообщения. При этом замена осуществляется так, чтобы потом по шифрованному сообщению можно было однозначно восстановить передаваемое сообщение.

Пусть, например, зашифровывается сообщение на русском языке и при этом замене подлежит каждая буква сообщения. Формально в этом случае шифр замены можно описать следующим образом. Для каждой буквы a исходного алфавита строится некоторое множество символов M _a так, что множества M _a и M _b попарно не пересекаются при a¹b, то есть любые два различные множества не содержат одинаковых элементов. Множество M _a называется множеством шифробозначений для буквы a.

Таблица

а	б	в	…	я
Ма	Мб	Мв	…	Мя

является ключом шифра замены. Зная ее, можно осуществить как зашифрование, так и расшифрование.

При зашифровании каждая буква a открытого сообщения, начиная с первой, заменяется любым символом из множества M _a. Если в сообщении содержится несколько букв a, то каждая из них заменяется на любой символ из M _a. За счет этого с помощью одного ключа можно получить различные варианты зашифрованного сообщения для одного и того же открытого сообщения. Часто M _a состоит из одного элемента.

Одним из первых шифров, известных из истории, был так называемый шифр Цезаря, для которого вторая строка (из рис. 1) является последовательностью, записанной в алфавитном порядке, но начинающейся не с буквы «а» (рис.2).

а	б	в	…	ь	э	ю	я
г	д	е	…	я	а	б	в

Рис. 2

В криптографии известны также блочные шифры простой замены. Например, одним из таких шифров является шифр, представленный таблицей всевозможных замен комбинаций заданного размера, составленных из бит сообщения. Например, таблица всевозможных замен трехбитовых комбинаций может иметь вид:

Принцип работы такого шифра следующий: исходный текст разбивается на тройки бит, затем каждая такая тройка ищется в левой колонке таблицы и заменяется на соответствующую тройку из правой колонки таблицы. Расшифрование выполняется аналогично: тройка бит ищется в правой колонке и заменяется на соответствующую тройку элементов из левой колонки.

Чем большее число бит обрабатывается за раз, тем сложнее вскрыть такой шифр. Однако для обработки n бит потребуется 2ⁿ строк таблицы, что может приводить к очень большим затратам памяти. Но такие шифры, работающие с небольшими блоками, являются крайне нестойкими. Поэтому их чаще всего используют в качестве составных частей более сложных и стойких шифров. В этом случае их называют блоками замен (S-блоками, англ. S-box).

При программировании S-бокса можно использовать его запись в виде таблицы, как показано выше. Однако заметим, что первый столбец содержит в себе номера элементов, записанные в двоичной системе счисления, от 0 до 7 (000-111). Поэтому достаточно хранить только второй столбец таблицы, записав его как одномерный массив, а элементами первого столбца считать просто номер соотв. элемента массива:

var Sbox: array[0..7] of integer; … Sbox[0]:= 7; Sbox[1]:= 1; Sbox[2]:= 2; Sbox[3]:= 6; Sbox[4]:= 5; Sbox[5]:= 4; Sbox[6]:= 3; Sbox[7]:= 0;

000 (=0) 111 (=7) 001 (=1) 001 (=1) 010 (=2) 010 (=2) 100 (=3) 110 (=6) 011 (=4) 101 (=5) 101 (=5) 100 (=4) 110 (=6) 011 (=3) 111 (=7) 000 (=0)

Тогда если a – это число, составленное из трех бит, подлежащих замене по этой таблице замен, то Sbox[a] – и есть соответствующая замена.

В дальнейшем таблицы замен будем задавать как одномерные массивы, согласно описанному выше принципу.

Для того, чтобы составить таблицу замен для расшифрования текста, сначала поменяем местами столбцы указанной нашей таблицы:

111 (=7)	000 (=0)
001 (=1)	001 (=1)
010 (=2)	010 (=2)
110 (=6)	100 (=3)
101 (=5)	011 (=4)
100 (=4)	101 (=5)
011 (=3)	110 (=6)
000 (=0)	111 (=7)

Затем проведем переупорядочение (сортировку по первому столбцу):

000 (=0)	111 (=7)
001 (=1)	001 (=1)
010 (=2)	010 (=2)
011 (=3)	110 (=6)
100 (=4)	101 (=5)
101 (=5)	011 (=4)
110 (=6)	100 (=3)
111 (=7)	000 (=0)

Т. обр., инициализация обратной таблицы замен будет иметь вид:

var SboxInv: array[0..7] of integer;

…

SboxInv[0]:= 7;

SboxInv[1]:= 1;

SboxInv[2]:= 2;

SboxInv[3]:= 6;

SboxInv[4]:= 5;

SboxInv[5]:= 4;

SboxInv[6]:= 3;

SboxInv[7]:= 0;

(в нашем случае она получилась такой же, как для прямой замены))

 

При выполнении работы требуется решить следующие задачи:

1. Реализовать функцию, выполняющую шифрование и расшифрование текста с помощью шифра Цезаря. Ключ шифра выбрать произвольно.

2. Реализовать функцию, выполняющую шифрование исходного текста с помощью 3-битовых замен. Таблицы замен придумать на свое усмотрение.

3. Реализовать функцию, выполняющую расшифрование текста, зашифрованного функцией, полученной на шаге 2.

 

Отчет по работе должен включать:

1. 2-минутное сообщение

2. программу-тест

 

Лабораторная работа № 4

 

Поточное шифрование. Алгоритм RC4.

 

Задание: Программно реализовать алгоритм поточного шифрования RC4.

 

Время выполнения: 1 пара.

 

RC4 - это потоковый шифр с переменным размером ключа, разработанный в 1987 году Роном Ривестом для RSA Data Security, Inc. В течение семи лет он находился в частной собственности, и подробное описание алго­ритма предоставлялось только после подписания соглашения о неразглашении.

В сентябре 1994 кто-то анонимно опубликовал исходный код в списке рассылки Cypherpunks. Он быстро распространился в телеконференции через Internet во всем мире. С тех пор алгоритм обсуждался и изучался в Usenet, распространял­ся на конференциях и служил в качестве учебного пособия на курсах по криптографии.

Описывать RC4 просто. В нем используется S-блок размером 256: S₀, S₁, …, S₂₅₅. Элементы представляют собой перестановку чисел от 0 до 255, а перестановка является функцией ключа переменной длины.

Опишем алгоритм инициализации S-блока, выполняемый в начале работы алгоритма. Сначала он заполняется линейно: S₀ = 0, S₁ = 1, …, S₂₅₅ = 255. Затем битами ключа заполняется другой 256-байтовый массив К, при необходимости для заполнения всего массива повторяя ключ: K₀, K₁, …, K₂₅₅.

Псевдокод этого алгоритма имеет вид:

j = 0;

for i = 0 to 255 do begin

j = (j + S_i + K_i) mod 256

поменять местами S_i и S_j

end

Эту идею можно обобщить на S-блоки и слова больших размеров.

Теперь опишем собственно алгоритм шифрования данных. В алгоритме применяются два счетчика, i, и j, с нулевыми начальными значениями.

Для генерации случайного байта K выполняется следующее:

i = (i + 1) mod 256

j = (j + S_i) mod 256

поменять местами S_i и S_j

t = (S_i + S_j) mod 256

K = S_t

Байт K используется в операции XOR с байтом открытого текста для получения шифротекста или в операции XOR с байтом шифротекста для получения открытого текста. Шифрование выполняется примерно в 10 раз быстрее, чем DES.

Напомним, что для определения значения отдельного байта числа необходима операция сдвига вправо и наложения маски (см. решение лабы 1.2). Маской будет число, составленное из восьми единичных младших битов, т.е. 11111111₂ = 255₁₀.

RC4 с ключом длиной не более 40 битов обладает специальным экспортным статусом. Название алгоритма является торговой маркой, поэтому каждый, кто напишет собственный код, должен назвать его как-то иначе. Различные внутренние документы RSA Data Security, Inc. до сих пор не были опубликованы.

 

При выполнении работы требуется решить следующие задачи:

1. Разработать алгоритм RC4.

 

Отчет по работе должен включать:

1. 2-минутное сообщение

2. программу-тест

 

 

Лабораторная работа № 5

 

Сеть Файстеля (Feistel). Итерация шифра ГОСТ 28147-89.

 

Задание: Ознакомиться с понятием сети Файстеля и программно реализовать один раунд шифра, использующего сеть Файстеля – шифра ГОСТ 28147-89.

 

Время выполнения: 1 пара.

 

В начале 1970-х годов компания IBM приступила к выполнению собственной программы научных исследований, посвященных защите информации в электронных сетях и криптографии. Команду разработчиков фирмы IBM, приступившую к исследованию систем шифрования с симметричной схемой использования ключей, возглавил Хорст Файстель. Результатом стала разработка новой оригинальной архитектуры построения симметричных шифров на базе необратимых преобразований, названной архитектурой Файстеля (более устоявшийся термин: сеть Файстеля или Feistel's network).

Архитектура сети

Построение сложных криптографически стойких, но обратимых преобразований представляет собой довольно трудоемкую задачу. По этой причине Файстель решил не искать решение проблемы обратимого преобразования данных, а попытаться найти схему шифрования, в которой такие преобразования не участвовали бы вовсе.

Рис. 1. Архитектура сети Файстеля

Изначально выбирается размер блока данных, который будет зашифрован за одну итерацию алгоритма шифрования. Обычно размер блока фиксирован и не изменяется во время работы алгоритма. Выбрав достаточно большого размера блок данных, его делят, например, пополам и затем работают с каждой из половинок. Если размер левой половинки равен размеру правой, такую архитектуру называют классической или сбалансированной сетью Файстеля. Если же деление блока данных происходит не на равные части, то такой алгоритм называют разбалансированной сетью Файстеля.

Предложенная им схема шифрования легко может быть продемонстрирована с помощью схемы шифрования (рис. 1).

На изображенной схеме буквами L_i и R_i обозначены левая и правая половинки исходных данных на i -м шаге последовательного преобразования. Каждый такой целый шаг называют раундом шифрования. Функция гаммирования обозначена через F_i, поскольку на каждом раунде может быть использована своя собственная функция. Ключ также имеет индекс i, но уже в силу того, что исходный ключ k может быть преобразован некоторым образом (говорят, развернут) в последовательность итерационных ключей (подключей).

Как видно из схемы, сначала с помощью функции гаммирования вырабатывают гамма-последовательность, которая зависит от итерационного ключа k_i и правой половины данных. После этого левая половинка просто суммируется с полученной гаммой по модулю, например, 2. Затем левая и правая половинки меняются местами.

На этом один цикл шифрования заканчивается. Поскольку за один раз обрабатывается только одна половина данных, желательно, чтобы число раундов было кратно двум. В таком случае каждая из половинок будет обработана одинаковое число раз.

Исходя из данного описания, преобразование данных одного раунда можно представить с помощью двух формул, выражающих новые значения левой и правой половинок блока шифруемых данных:

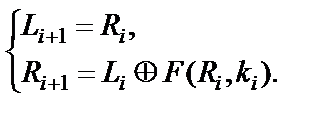
Использование сети Файстеля

Предложенная архитектура стала использоваться при создании разнообразных блочных шифров. В качестве примера можно привести такие шифрсистемы, как DES, ГОСТ 28147–89.

Одна из ценностей преобразований, реализуемых сетью Файстеля, заключается в том, что даже если функция F не является обратимой функцией, само преобразование обратимо. И обратное преобразование, используемое для расшифровки, может быть описано следующим образом:

В большинстве шифров с архитектурой сети Файстеля используемая функция F в течение каждого раунда зависит только от одного из подключей, вырабатываемых из основного ключа шифра. Это свойство на самом деле не является основополагающим или положительно влияющим на стойкость шифра.

Естественным путем увеличения сложности анализа сетей Файстеля является следующий метод. К выходному значению F прибавляют по некоторому модулю значение итерационного подключа для текущего раунда и затем полученное значение подают на вход функции F следующего раунда шифрования.