Аналитическое (символьное) решение дифференциальных уравнений осуществляется с помощью команды DSolve, которая имеет три формата DSolve[eqn,y,x] - решает обыкновенное дифференциальное уравнение eqn относительно неизвестной функции y[x] независимой переменной x;
DSolve[{eqn1,eqn2,…,},{y1,y2,…},x] - решает систему обыкновенных дифференциальных уравнений {eqn1,eqn2,…} относительно неизвестных функций {y1[x],y2[x],…} независимой переменной x;
DSolve[eqn,y,{x1,x2,…}] - решает дифференциальное уравнение в частных производных eqn относительно неизвестной функции y[x1,x2,…] независимых переменных x1,x2, ….

Решение представлено в виде подстановки, константа интегрирования обозначена как C[1]. Если желательно другое обозначение для этой константы, то следует использовать опцию DSolveConstants→K:

Для использования полученного решения можно, например, присвоить подстановке некоторое имя

и определить соответствующую функцию

Проверка показывает, что цель достигнута:

Если необходимо решить дифференциальное уравнение с определенными граничными (или начальными) условиями, то их надо определить в списке решаемых уравнений, например, следующая команда интегрирует уравнение y’[x]==ay[x] с условием y[0]=5:



Константа интегрирования при этом оказывается автоматически определенной. Если нужно решить систему дифференциальных уравнений


то соответствующая команда имеет вид

Численное решение дифференциальных уравнений осуществляется с помощью команды NDSolve, которая имеет три формата:
NDSolve[eqns,y[x],{x,a,b}] - находит приближенное решение обыкновенного дифференциального уравнения eqns (с начальными условиями) относительно неизвестной функции y[x] независимой переменной x в интервале [a,b];
NDSolve[{eqn1,eqn2,…},{y1,y2,…},{x,a,b}] - численно решает систему обыкновенных дифференциальных уравнений {eqn1,eqn2,…) с начальными условиями относительно неизвестных функций {y1[x],y2[x],…} независимой переменной x на интервале [a,b];
NDSolve[eqn,y,{x1,x2,…}] - численно решает дифференциальное уравнение в частных производных eqn относительно неизвестной функции y[x1,x2,…] независимых переменных x1,x2, ….
Так, дифференциальное уравнение третьего порядка с начальными условиями можно численно проинтегрировать командой




Результат интегрирования Mathematica выводит в форме некоторой интерполяционной функции, для которой можно построить график:

Индивидуальные задания:
1. Решить уравнение символьно и численно уравнение:
| № | Задание | № | Задание |

| 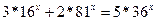
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
2. Решить систему уравнений:
| № | Задание | № | Задание |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 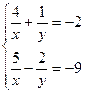
|
3. Решить символьно и численно дифференциальные уравнения:
| № | Задание | № | Задание |
 ; ;

|  ; ;

| ||
 ; ;

|  ; ;

| ||
 ; ;

|  ; ;

| ||
 ; ;

|  ; ;

| ||
 ; ;

|  ; ;

| ||
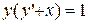 ; ;

|  ; ;

| ||
 ; ;

|  ; ;

|
4. Решить дифференциальное уравнение:
| № | Задание | № | Задание |

| 
| ||
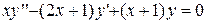
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|






