Переменный электрический ток

Переменный ток – это пример вынужденных колебаний в электрической цепи.

Пусть к электрической цепи приложено переменное напряжение:U=U_max*cos ωt, т.к. изменения напряжения и силы тока происходят медленно по сравнению со скоростью распространения электромагнитных взаимодействий, то значение напряжения и силы тока во всей цепи будут одинаковы. Такой ток называется квазистационарным. Для него выполняются законы Ома и Кирхгоффа.

1. Сопротивление R в цепи переменного тока.

Если напряжение U=U_max*cos ωt, то по закону Ома

Отступление: Если есть колебания x = A*cos(ω t + φ), то на графике:

2. Катушка индуктивности l в цепи переменного тока.

В этом случае в катушке возникнет ЭДС самоиндукции:

По закону Ома для цепи содержащей ЭДС: IR = (φ₁ – φ₂) + ε

По условию: φ₁ – φ₂ = U_max*cosωt где R→0

Получаем:

Подставим:

Проинтегрируем:

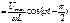
Следовательно:

а) Для цепи содержащей L выполняется закон Ома если

считать что сопротивление , R_L – индуктивное реактивное сопротивление.

б) Напряжение на катушке опережает ток по фазе на π/2.

3. Конденсатор цепи переменного тока.

Если к конденсатору приложить переменное напряжение, то он будет перезаряжаться и в цепи будет течь переменный ток. Напряжение на конденсаторе равно внешнему напряжению

Сила тока: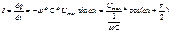

Следовательно:

а) Для цепи содержащей конденсатор выполняется закон Ома если считать что сопротивление .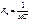

б) Напряжение на конденсаторе отстаёт по фазе от тока на π/2.

4. Цепь переменного тока содержащая R,L и C включенных последовательно.

Сила тока в каждом элементе одинакова, а напряжение складывается, но не алгебраически, а векторно.

По теореме Пифагора: U² = U_R² +(U_L – U_C)²

По закону Ома: U_R = IR; U_L = IR_L = IωL; U_C = IR_C = I/ωC

Подставим:

Сократим I² и получим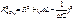

Величина: 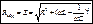- полное сопротивление цепи переменного тока.

Из чертежа: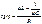

Если в цепи L = 1/ωC, то Z=R – принимает минимальное значение(резонансное напряжение)

5. Мощность переменного тока.

Если ток переменный, то мощность равна: P(t) = U(t)*I(t) т.к. U = U_max*cosωt I = I_max*cos(ωt-φ)

Следовательно мгновенная мощность равна:

P(t)=U_maxI_max*cosωt*cos(ωt-φ)= =U_maxI_max*cosωt*(cosωt*cosφ+sinωt*sinφ)=

=U_maxI_max(cos²ωt* cosφ+cosωt*sinωt*sinφ)

Значение имеет не мгновенная мощность, а средняя мощность за один период.

Среднее значение функции: cos²ωt=1/2.

Среднее значение функции: cosωt*sinωt=1/2sin2ωt=0

Следовательно средняя мощность переменного тока: <P>=1/2U_max*I_max*cosφ

Множитель cosφ называется коэффициентом мощности.

Это можно записать так:

Величины: 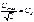– действующее значение напряжения;

– действующее значение силы тока.