Метод интегрирования подстановкой заключается во введение новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводится (в случае «удачной» подстановки). Умение правильно определить подстановку приобретается практикой. Тем не менее, рассмотрим несколько общих подходов (назовем их правилами) к данному методу, что позволит систематизировать умение интегрировать методом подстановки и определять новую переменную.
2.2.10 Интегрирование функций (табличные интегралы) к аргументу, которых прибавляется постоянная величина
Рассмотрим некоторые табличные интегралы к аргументу, которых прибавляется (вычитается) постоянная величина 
.
2.2.1 
Решение. Введем подстановку x+2 = t (*). Найдем дифференциал от правой и левой частей равенства (*), получим:
, 
,
Подставим вместо x+2 и 
их значения через t в данный интеграл, получим:
Легко заметить, что формулы интегрирования сохраняют инвариантность (вид). В данном случаи степенная функция интегрируется по аргументу (х+2).
2.2.2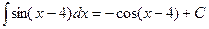 
Правило 1
Если к аргументу подынтегральной функции прибавляется (вычитается) постоянная величина  , то формулы интегрирования сохраняют инвариантность
|
2.2.3 
2.2.20 Интегрирование функций (табличные интегралы) аргумент, которых умножается на постоянную величину
Рассмотрим некоторые табличные интегралы аргумент, которых умножается на постоянную величину 
2.2.4 
Решение. Введем подстановку 3x = t (*). Найдем дифференциал от правой и левой частей равенства (*), получим:
, 
, 
Подставим вместо 
и их значения через t в данный интеграл, получим:
| заменим t его выражением через x|=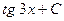 
Замечание В дальнейшем процедура решения, представленная, в примерах 32, 35 будет записываться в виде:
.
Правило 2
Если аргумент подынтегральной функции умножается на постоянную величину  , то формулы интегрирования сохраняют инвариантность, результат интегрирования умножается на число  .
|
2.2.6 
2.2.7 
Замечание. Правила 1 и 2 к подынтегральной функции могут применяться одновременно.
2.2.8 
2.2.9 
2.2.10 
2.2.11 
2.2.12 
При интегрирование тригонометрических функций 
и 
применяются формулы понижения степени:
и 
Выполните самостоятельно
| 
| 
| 
| ||||
| 
| 
| 
|
2.2.30 Интегралы вида: 
, 
Интегралы данного вида находятся путем выделения полного квадрата из данного
квадратного трехчлена по формуле:
(**) и применения правил 1,2.
Интеграл , после выделения полного квадрата сводится к формулам 9 или 10.
Интеграл , после выделения полного квадрата сводится к формулам 8 или
11.
2.2.14 
| выделите в знаменатели ПФ полный квадрат по формуле (**)| = 
2.2.16 
=
(сомножитель (-1) внесем в квадратные скобки, получим 
) =
Выполните самостоятельно
| 
| 
| 
|
2.2.40 Интегрирование дробных функций (рациональных или иррациональных), когда в знаменатели или под корнем в знаменатели стоит функция, производная которой равна числителю (или приводится к числителю).
Интегралы этого вида находятся путем замены многочлена стоящего в знаменателе ПФ новой переменной
2.2.17 
Замечаем, что производная знаменателя ПФ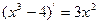 
, отличается от числителя только постоянным множителем. Выполним интегрирование, за новую переменную примем 
2.2.18 
Легко заметить, что если в числителе стоит производная знаменателя, то интеграл всегда равен натуральному логарифму знаменателя.
2.2.19 
2.2.20 
Правило 3
Если под знаком интеграла стоит дробная функция(рациональная или иррациональная), в знаменателе которой или под корнем в знаменателе содержится функция, производная которой равна числителю(или приводится к числителю), то интеграл вычисляется способом замены переменной, причем функция, стоящая в знаменатели обозначается за t.
 где  или  где , то 
|
Выполните самостоятельно
| 
| 
| 
| ||||
| 
| 
| 
|
2.2.50 Интегралы вида: 
Р ассмотрим интегралы, в которых ПФ представлена как произведение сложной функции и производной ее промежуточного аргумента. В этом случае промежуточный аргумент принимается за новую переменную t.
Например 
Функция 
сложная, ее промежуточный аргумент равен 
, производная которого 
содержится в ПФ, поэтому интеграл сводится к табличному подстановкой 
. Действительно
= 
Рассмотрите интегралы данного вида
2.2.23 
= 
2.2.25 
2.2.26 
2.2.27 
2.2.28 
2.2.29 
Выполните самостоятельно
| 
| 
| 
| ||||
| 
| 
| 
| ||||
| 
| 
| 
| ||||
| ò 
| 
| 
|
Правило 4
Если под знаком интеграла стоит сложная функция в произведение с производной своего промежуточного аргумента, то интеграл вычисляется способом замены переменной, причем промежуточный аргумент обозначается за t.
 , 
|
Замечание Используя правило 4 вычисляются интегралы, которые с помощью подстановки сводятся к табличным интегралам по формулам 8-11. (Обратите внимание, что данные интегралы имеют «специфический» вид).
2.2.30 
2.2.31 
2.2.32 
2.2.33 
Выполните самостоятельно
| 
| 
| 
| ||||
| 
| 
| 
| ||||
| 
| 
| 
|
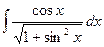
Указания:
66 Представьте 
, обозначьте 
68 Представьте 
, обозначьте 
70 Обозначьте 
и распишите 
2.2.60 Интегрирование простейших иррациональных функций
В данном пункте рассмотрим интегралы вида: 
, которые находятся
подстановкой 
, 
, 
(Правило 5)
При интегрировании иррациональных функций с помощью подстановки необходимо
избавиться от иррациональности (корня).
2.2.34 
2.2.35 
Замечание. Этот способ интегрирования применяется и в том случае, когда под корнем стоит трансцендентная функция.
2.2.37 
Выполните самостоятельно
| 
| 
| 
| ||||
| 
| 
| 
|
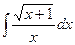
2.2.70 Интегрирование с помощью преобразования подынтегральной функции
Иногда, прежде чем найти интеграл необходимо выполнить преобразования ПФ (применить формулы элементарной математики, почленное деление числителя ПФ на знаменатель).
2.2.38 
;
Обозначим данный интеграл I, тогда
2.2.39 
;
Выполните самостоятельно
| 
| 
| 
| ||||
| 
| 
| 
| ||||
| 
| 
| 
|
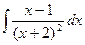
Указания:
86 Обозначьте 
, тогда 
88Обозначьте 
, тогда 
89 Обозначьте 
и распишите 
90 Обозначьте 
, тогда 
91 Помножьте числитель и знаменатель ПФ на 2 и воспользуйтесь формулой 
ВНИМАНИЕ Если вы хорошо овладели интегрированием методом подстановки, то
должны уметь применять этот метод и в нестандартных интегралах.
2.2.40 
Способ 1 
Способ 2 
Способ 3 
, далее как способом 2.
