Этот вариант применяют, когда в дополнительный алгоритм выносится участок вычислений, содержащий одну или несколько формул с одним конечным результатом. Рассмотрим конкретную задачу (10.1) вычисления факториала.
Рис.10.9. Схема взаимодействия головной функции с пользовательскими
Постановка задачи
Вычислить значение функции:
z = ln a + n! + m! – (k – m)! – 0.2 a
если a=16.9; n=5; m=4; k=10.
Формирование математической модели
Исходные данные:
a=16.9;
n=5;
m=4;
k=10.
Расчетные зависимости
; Формулы
; вычисления
. факториалов.
Детализация
вычислительной
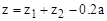зависимости.
Выбор метода решения
Анализ математической модели показывает необходимость троекратного последовательного вычисления значения факториала n!, m! или (k-m)! отдельно для фактических параметров n, m или (k-m).
Известно, что вычисление значения 
осуществляется смешанным процессом накопления произведения – ветвлением в арифметическом цикле.
Участок вычисления факториала требуется оформить дополнительным алгоритмом (функцией), именованным fakt, а используемый в нём аргумент (формальный параметр) желательно назвать f.
Следовательно, рациональный метод решения задачи – вычислительный процесс с одним подпроцессом при использовании основного алгоритма с обращениями fakt(n), fakt(m), fakt(k-m) и дополнительного алгоритма с формальным параметром f.
Составление алгоритма решения
Выбранный метод решения с использованием одного подпроцесса реализуется в виде отдельных алгоритмов – основного и дополнительного (рис. 10.11).
Рис. 10.11. Схема алгоритма задачи о факториалах
Основной алгоритм использует локальные переменные a, z1, z2, z и фактические параметры n, m, k – m. Обращения к дополнительному алгоритму выполняются из арифметических выражений двух блоков основного.
Содержимое начального блока дополнительного алгоритма (fakt(t)) определяет его название и используемый формальный параметр.
В дополнительном алгоритме наряду с формальным параметром f используются локальные (местные) переменные fi и i. Первая обозначает вычисляемое в цикле значение факториала, а вторая является текущим значением последнего сомножителя. В конечном блоке указан возвращаемый операнд (переменная fi).
Программирование задачи
Программирование задачи требует двух пользовательских функций:
· головной – для реализации основного алгоритма;
· дополнительной – для выполнения вспомогательного алгоритма.
При этом головная функция должна содержать обращение к дополнительной (ее вызов).
Структура вызова функции:
имя ([a1,..., ai,..., an])
где имя – идентификатор вызываемой функции;
a1... ai... an – список фактических параметров (аргументов) основной функции, численные значения которых передаются в дополнительную;
,, – разделители элементов списка;
() – ограничители аргументов;
[ ] – признак необязательности содержимого.
Каждая из функций Си/Си++ представляется одной из упрощенных структур:
| Левый вариант | Правый вариант |
| [тип] имя([тип b1,...,тип bi,...,тип bn]) { тело функции [return [РВ];] } | [тип] имя([b1,...,bi,...,bn]) [описатели bi] { тело функции [return [РВ];] } |
где имя – идентификатор (название) функции;
тип – описатель типа функции (результата);
тип bi – элемент списка формальных параметров, используемых в вычислениях (действиях) тела функции с указанием типа;
, – разделитель элементов списка.
описатели bi – операторы описания типов формальных параметров, выполненные вне заголовка;
() – ограничители списка формальных параметров;
тело функции – основная часть (совокупность операторов), реализующая вынесенные в отдельный алгоритм вычисления (действия);
return РВ; – оператор возврата (return) в вызывающую функцию результата вычислений РВ (выражения);
[ ] – признак необязательности содержимого;
{ } – ограничители тела функции.
Заголовок функции– первая строка ее структуры.
Различия заголовочных структур функций обусловлены различными средствами машинной обработки создаваемых программ. Большинство средств поддерживают оба варианта.
