Интегрирование по частям. Примеры решений
Итак, научимся интегрировать по частям. Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Под рукой должны быть: Таблица интегралов и Таблица производных. Материал будет изложен последовательно, просто и доступно, и в интегрировании по частям у вас в дальнейшем не будет особых трудностей.
Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное.
По частям берутся интегралы следующих видов:
1) 
, 
, 
– логарифм, логарифм, умноженный на какой-нибудь многочлен.
2) 
, 
– экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде 
– показательная функция, умноженная на многочлен, но на практике под интегралом чаще встречается буква «е».
3) 
, 
, 
– тригонометрические функции, умноженные на многочлен.
4) 
, 
– обратные тригонометрические функции, умноженные на многочлен.
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Пример 1
Найти неопределенный интеграл.
Решение:
Прерываем решение на промежуточные объяснения.
Используем формулу интегрирования по частям: 
Формула применяется слева направо
Смотрим на левую часть: 
. Очевидно, что в нашем примере
(и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за 
, а что-то за 
.
В интегралах рассматриваемого типа за всегда обозначается логарифм.
Технически оформление решения реализуется следующим образом, в столбик записываем:
То есть, за мы обозначили логарифм, а за – оставшуюся часть подынтегрального выражения.
Следующий этап: находим дифференциал 
:
Теперь находим функцию 
. Для того чтобы найти функцию необходимо проинтегрировать правую часть нижнего равенства :
Теперь открываем наше решение и конструируем правую часть формулы: 
. Вот образец чистового решения с небольшими пометками:
Интегрируем по частям: 
(*)= 
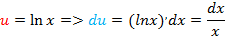
Как видите, применение формулы интегрирования по частям, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Пример 2
Найти неопределенный интеграл.
Подынтегральная функция представляет собой произведение логарифма на многочлен.
Решение:
Еще один раз подробно распишем порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам.
Как уже говорилось, за необходимо обозначить логарифм (то, что он в степени – значения не имеет). За обозначаем оставшуюся часть подынтегрального выражения.
Записываем в столбик:
Сначала находим дифференциал :
Теперь находим функцию , для этого интегрируем правую часть нижнего равенства :
Для интегрирования мы применили простейшую табличную формулу 
Теперь всё готово для применения формулы . Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью 
:
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за в похожих ситуациях всегда обозначается логарифм.
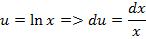
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей скобке 
, и эти скобки нужно корректно раскрыть.
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Пример 3
Найти неопределенный интеграл.
, 
Это примеры для самостоятельного решения.
Вроде бы в примере подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен.
Интегралы от экспоненты, умноженной на многочлен
Общее правило: за 
всегда обозначается многочлен
Пример 4
Найти неопределенный интеграл.
Решение:
Используя знакомый алгоритм, интегрируем по частям:
Если возникли трудности с интегралом 
, то следует вернуться к теме «Метод замены переменной в неопределенном интеграле».
Преобразуем ответ:
Пример считается решенным, когда взят последний интеграл. Не преобразованный ответ ошибкой не будет.
Пример 5
Найти неопределенный интеграл.
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что 
– сложная функция.
Это основные сведения про экспоненту. Не забывайте, что экспонента и натуральный логарифм взаимно-обратные функции.
