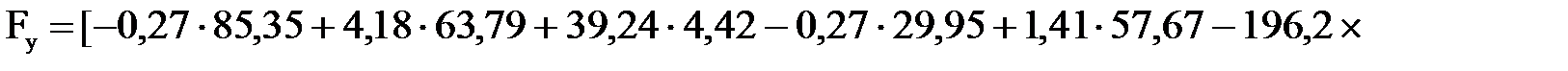Кинетостатический анализ рычажного механизма
Задачами кинетостатического анализа механизма являются:
1) определение весов звеньев механизма;
2) определение моментов сил инерции и сил инерции звеньев в одном из трех положений механизма;
3) определение реакций в кинематических парах и уравновешивающей силы методом планов сил;
4) определение с помощью метода Н. Е. Жуковского уравновешивающей силы для исследуемого положения механизма;
5) сравнение значений уравновешивающей силы, полученных по методу планов сил и по методу Н. Е. Жуковского.
Определение весов звеньев механизма
Определим вес звеньев механизма по формуле:
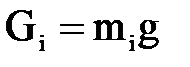 , (4.1)
, (4.1)
где 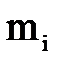 - масса i-го звена, кг;
- масса i-го звена, кг;
g - ускорение свободного падения, равное 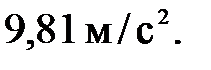
Массы звеньев и значения их весов приведены в таблице 9.
Таблица 9 - Массы и веса звеньев
| Номер звена | |||
| Масса звена, кг | |||
| Вес звена, Н | 39,24 | 196,2 | 39,24 |
Определение моментов сил инерции и сил инерции звеньев в одном из трех положений механизма
Силу инерции i-го звена находим по формуле:
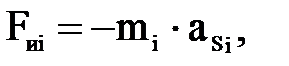 (4.2)
(4.2)
где 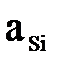 - ускорение центра масс i-го звена,
- ускорение центра масс i-го звена, 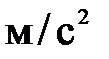 .
.
Знак “ - ” говорит о том, что вектор силы инерции  направлен противоположно вектору ускорения
направлен противоположно вектору ускорения 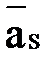 .
.
Значения ускорений точек центров масс звеньев и сил инерций, приложенных в этих точках представлены в таблице 10.
Таблица 10 - Значения ускорений центров масс и сил инерций
| Номер звена | ||
| Длина вектора на плане ускорений, мм | 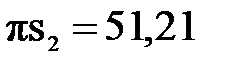
| 
|
Величина ускорения, 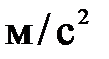
| 1,045 | 1,712 |
| Сила инерции, Н | 4,18 | 34,24 |
Ускорение точки 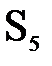 равно нулю, так эта точка совпадает с точкой стойки
равно нулю, так эта точка совпадает с точкой стойки 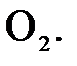
Момент сил инерции i-го звена находим по формуле:
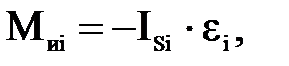 (4.3)
(4.3)
где  - момент инерции i-го звена относительно оси, проходящей через центр масс,
- момент инерции i-го звена относительно оси, проходящей через центр масс, 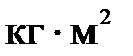 ;
;
 - угловое ускорение i-го звена,
- угловое ускорение i-го звена, 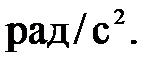
Знак “ - ” говорит о том, что момент силы инерции  противоположно направлен угловому ускорению
противоположно направлен угловому ускорению 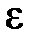 .
.
Угловое ускорение i-го звена определим по формуле:
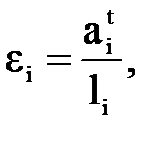 (4.4)
(4.4)
где 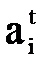 - тангенциальное ускорение i-го звена,
- тангенциальное ускорение i-го звена,  ;
;
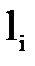 - длина i-го звена.
- длина i-го звена.
Тогда для 2-го, 4-го и 5-го звеньев формула (4.4) будет выглядеть следующим образом:
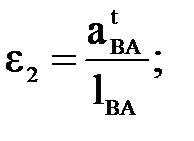 (4.5)
(4.5)
 (4.6)
(4.6)
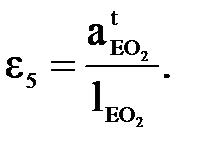 (4.7)
(4.7)
Подставляя числовые значения в формулы (4.5) - (4.7), получим соответственно
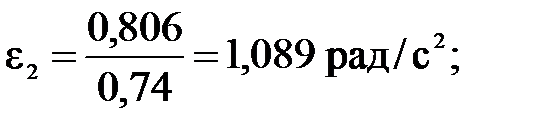
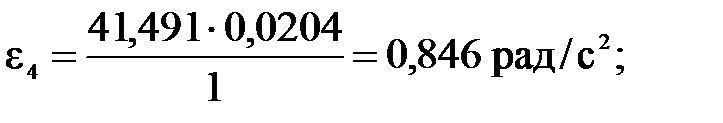
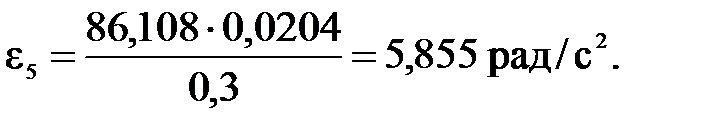
Момент инерции i-го звена относительно оси, проходящей через центр масс, находим по формуле:
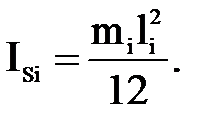 (4.8)
(4.8)
Значения моментов сил инерции звеньев, их осевые моменты и угловые ускорения представлены в таблице 11.
Таблица 11 - Значения сил инерции звеньев, их осевые моменты и угловые ускорения
| Номер звена | |||
Угловое ускорение, 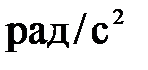
| 1,089 | 0,846 | 5,855 |
Осевой момент инерции, 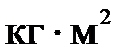
| 0,18 | 1,67 | 0,03 |
Момент сил инерции, 
| 0,2 | 1,41 | 0,18 |
Определение реакций в кинематических парах и уравновешивающей силы методом планов сил
Определение реакций в кинематических парах начинаем с рассмотрения равновесия группы, состоящей из звеньев 4 и 5. На звенья этой группы действуют силы тяжести  сила инерции
сила инерции 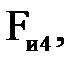 моменты сил инерции
моменты сил инерции 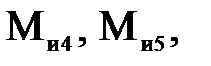 полезный момент сопротивления
полезный момент сопротивления 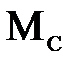 , реакции
, реакции 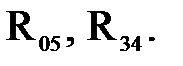
Условие равновесия группы выражается следующим равенством:
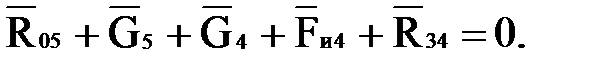 (4.9)
(4.9)
Так как в данном уравнении неизвестны величина и линия действия сил 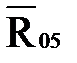 и
и 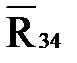 , то для решения этого уравнения реакции
, то для решения этого уравнения реакции 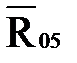 и
и  раскладываем на две составляющие:
раскладываем на две составляющие:
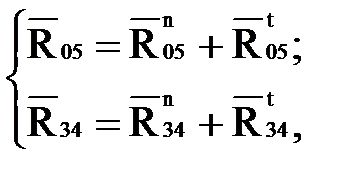 (4.10)
(4.10)
где  - составляющие, действующие вдоль оси звеньев;
- составляющие, действующие вдоль оси звеньев;
 - составляющие, действующие перпендикулярно к осям звеньев.
- составляющие, действующие перпендикулярно к осям звеньев.
Тогда уравнение (4.9) примет вид:
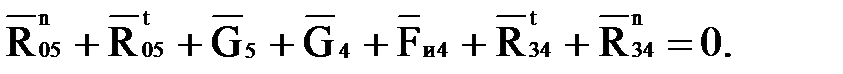 (4.11)
(4.11)
Масштабный коэффициент длин для данной группы равен 
Составляющую 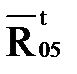 определяем из уравнения равновесия звена 5 относительно точки Е:
определяем из уравнения равновесия звена 5 относительно точки Е:
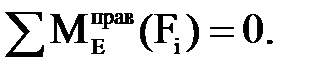
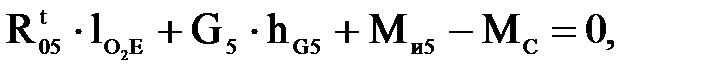 (4.12)
(4.12)
где 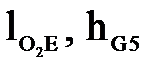 - плечи действия сил, м.
- плечи действия сил, м.
Выразим из формулы (4.12)  :
:
 (4.13)
(4.13)
Подставляя числовые значения, получим

Составляющую  определяем из уравнения равновесия звена 4 относительно точки Е:
определяем из уравнения равновесия звена 4 относительно точки Е:

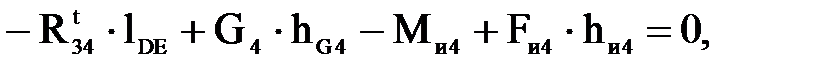 (4.14)
(4.14)
где  - плечи действия сил, м.
- плечи действия сил, м.
Выразим из формулы (4.12)  :
:
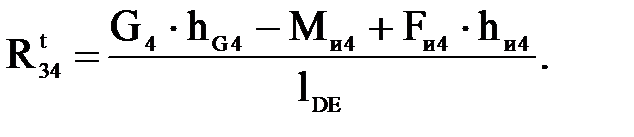 (4.15)
(4.15)
Подставляя числовые значения, получим

Решаем графически уравнение (4.11), для чего строим план сил. Из начала вектора 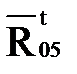 проводим линию действия силы
проводим линию действия силы 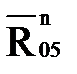 , параллельную звену 5, а из конца вектора
, параллельную звену 5, а из конца вектора  проводим линию действия силы
проводим линию действия силы 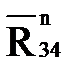 , параллельную звену 4. Пересечение двух линий определяет положение конца вектора
, параллельную звену 4. Пересечение двух линий определяет положение конца вектора  и начала вектора
и начала вектора 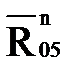 .
.
Масштабный коэффициент сил для данной группы равен 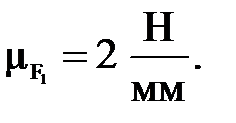
Результаты вычислений приведены в таблице 12.
Таблица 12 - Значения сил для группы I
| Сила | Длина вектора на плане, мм | Величина силы, Н |

| 96,89 | 193,78 |

| 55,60 | 111,20 |

| 19,62 | 39,24 |

| 98,10 | 196,20 |

| 17,12 | 34,24 |
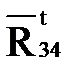
| 48,52 | 97,04 |
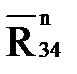
| 93,91 | 187,82 |
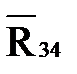
| 105,71 | 211,42 |
Рассмотрим равновесие группы, состоящей из звеньев 3 и 2. На звенья этой группы действуют сила тяжести 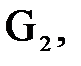 сила инерции
сила инерции  момент сил инерции
момент сил инерции 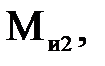 реакции
реакции 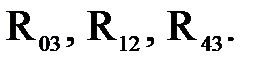
Условие равновесия группы выражается следующим равенством:
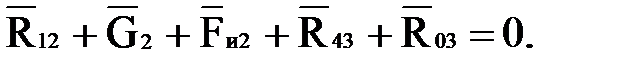 (4.16)
(4.16)
Так как в данном уравнении неизвестны величина  , величина и линия действия силы
, величина и линия действия силы  , то для решения этого уравнения реакцию
, то для решения этого уравнения реакцию  раскладываем на две составляющие:
раскладываем на две составляющие:
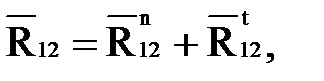 (4.17)
(4.17)
где 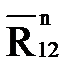 - составляющая, действующая вдоль звена 2;
- составляющая, действующая вдоль звена 2;
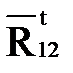 - составляющая, действующая перпендикулярно к звену 2.
- составляющая, действующая перпендикулярно к звену 2.
Тогда уравнение (4.16) примет вид:
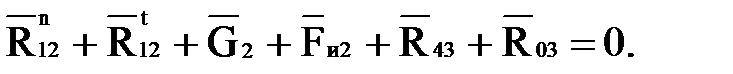 (4.18)
(4.18)
Масштабный коэффициент длин для данной группы равен 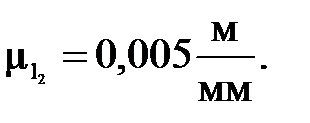
Составляющую 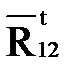 определяем из уравнения равновесия звена 2 относительно точки В:
определяем из уравнения равновесия звена 2 относительно точки В:

 (4.19)
(4.19)
где 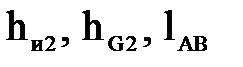 - плечи действия сил, м.
- плечи действия сил, м.
Выразим из формулы (4.19)  :
:
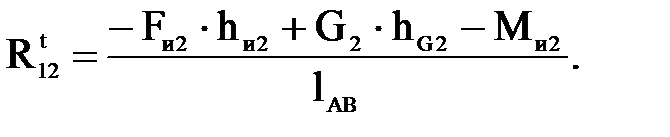 (4.20)
(4.20)
Подставляя числовые значения, получим

Решаем графически уравнение (4.18), для чего строим план сил. Из начала вектора 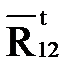 проводим линию действия силы
проводим линию действия силы  , параллельную звену 2, а из конца вектора
, параллельную звену 2, а из конца вектора  проводим линию действия силы
проводим линию действия силы 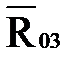 , перпендикулярную к звену 3. Пересечение двух линий определяет положение конца вектора
, перпендикулярную к звену 3. Пересечение двух линий определяет положение конца вектора 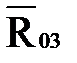 и начала вектора
и начала вектора 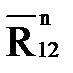 .
.
Масштабный коэффициент сил для данной группы равен 
Результаты вычислений приведены в таблице 13.
Таблица 13 - Значения сил для группы II
| Сила | Длина вектора на плане, мм | Величина силы, Н |
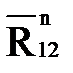
| 82,73 | 82,73 |
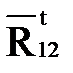
| 17,74 | 17,74 |
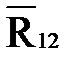
| 84,61 | 84,61 |

| 39,24 | 39,24 |
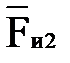
| 4,18 | 4,18 |
Продолжение таблицы 13
| Сила | Длина вектора на плане, мм | Величина силы, Н |
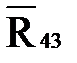
| 211,42 | 211,42 |
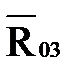
| 301,11 | 301,11 |
Рассмотрим равновесие ведущего звена. На него действуют уравновешивающая сила  реакции
реакции 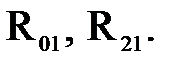
Условие равновесия ведущего звена выражается следующим равенством:
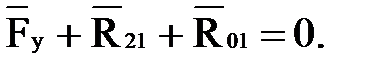 (4.21)
(4.21)
Так как в данном уравнении неизвестны величина  , величина и линия действия силы
, величина и линия действия силы 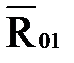 , то для решения этого уравнения реакцию
, то для решения этого уравнения реакцию 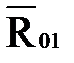 раскладываем на две составляющие:
раскладываем на две составляющие:
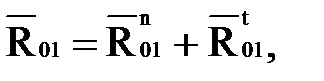 (4.22)
(4.22)
где 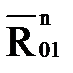 - составляющая, действующая вдоль кривошипа 1;
- составляющая, действующая вдоль кривошипа 1;
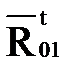 - составляющая, действующая перпендикулярно к кривошипу 1.
- составляющая, действующая перпендикулярно к кривошипу 1.
Тогда уравнение (4.21) примет вид:
 (4.23)
(4.23)
Масштабный коэффициент длин для данной группы равен 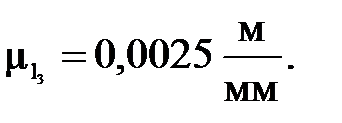
Составляющую  определяем из уравнения моментов всех сил относительно точки А:
определяем из уравнения моментов всех сил относительно точки А:
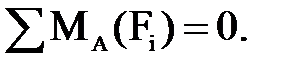
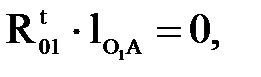 (4.24)
(4.24)
где  - плечо действия силы, м.
- плечо действия силы, м.
Из уравнения (4.24) получаем, что 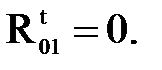
Решаем графически уравнение (4.23), для чего строим план сил. Из начала вектора 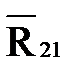 проводим линию действия силы
проводим линию действия силы  , перпендикулярную к кривошипу 1, а из конца вектора
, перпендикулярную к кривошипу 1, а из конца вектора 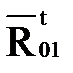 , который совпадает с концом вектора
, который совпадает с концом вектора 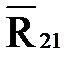 проводим линию действия силы
проводим линию действия силы  , параллельную кривошипу 1. Пересечение двух линий определяет положение конца вектора
, параллельную кривошипу 1. Пересечение двух линий определяет положение конца вектора 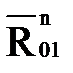 и начала вектора
и начала вектора 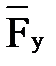 .
.
Масштабный коэффициент сил для данной группы равен 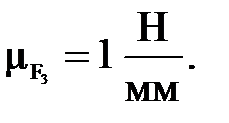
Результаты вычислений приведены в таблице 14.
Таблица 14 - Значения сил для ведущего звена
| Сила | Длина вектора на плане, мм | Величина силы, Н |

| 70,94 | 70,94 |

| 84,61 | 84,61 |
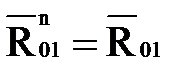
| 46,11 | 46,11 |
Определение с помощью метода Н. Е. Жуковского уравновешивающей силы для исследуемого положения механизма
Определим с помощью метода Н. Е. Жуковского уравновешивающую силу для седьмого положения механизма. Для этого повернем план скоростей для исследуемого положения на  против хода часовой стрелки и будем рассматривать его как жесткую фигуру. На повернутый план скоростей в характерные точки переносим все заданные силы, действующие на механизм (за исключением реакций), включая силы инерции и уравновешивающую силу. Моменты сил инерции
против хода часовой стрелки и будем рассматривать его как жесткую фигуру. На повернутый план скоростей в характерные точки переносим все заданные силы, действующие на механизм (за исключением реакций), включая силы инерции и уравновешивающую силу. Моменты сил инерции 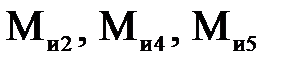 и полезный момент сопротивления
и полезный момент сопротивления 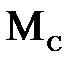 представим в виде пар сил
представим в виде пар сил 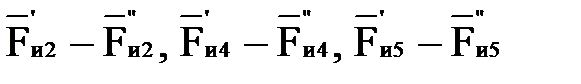 и
и 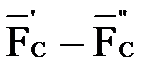 соответственно, приложенных перпендикулярно к звеньям механизма.
соответственно, приложенных перпендикулярно к звеньям механизма.
Определим величину этих сил по формуле:
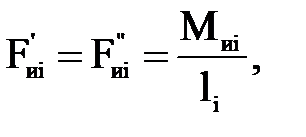 (4.25)
(4.25)
где 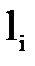 - длина i-го звена.
- длина i-го звена.
Тогда для 2-го, 4-го и 5-го звеньев формула (4.25) будет выглядеть следующим образом:
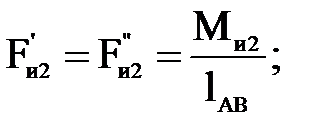 (4.26)
(4.26)
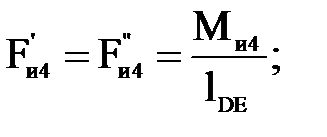 (4.27)
(4.27)
 (4.28)
(4.28)
Величину силы полезного сопротивления определим по формуле:
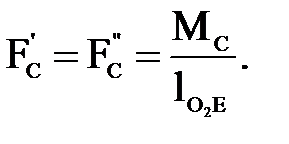 (4.29)
(4.29)
Подставляя числовые значения в формулы (4.26) - (4.29), получим соответственно
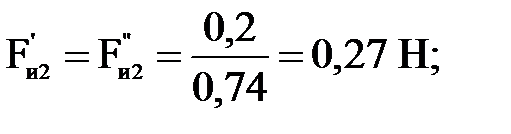
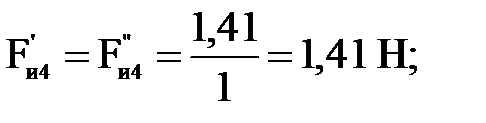
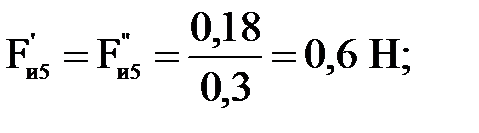
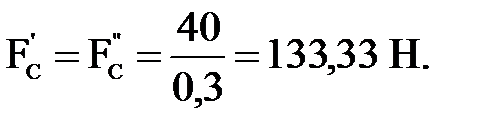
Уравновешивающую силу  определяем из уравнения моментов всех сил относительно полюса р плана скоростей:
определяем из уравнения моментов всех сил относительно полюса р плана скоростей:
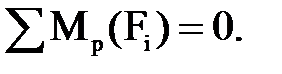

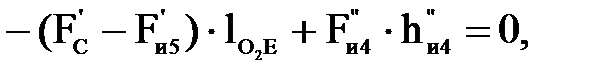 (4.30)
(4.30)
где 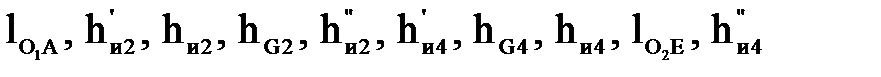 - плечи действия сил, взятые с чертежа, мм.
- плечи действия сил, взятые с чертежа, мм.
Выразим из формулы (4.30) 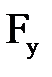 :
:

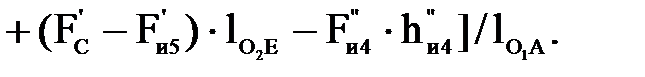 (4.31)
(4.31)
Подставляя числовые значения, получим