Магнитное поле движущегося заряда может возникать вокруг проводника с током. Так как в нем движутся электроны, обладающие элементарным электрическим зарядом. Также его можно наблюдать и при движении других носителей зарядов. Например, ионов в газах или жидкостях. Это упорядоченное движение носителей зарядов, как известно, вызывает в окружающем пространстве возникновение магнитного поля. Таким образом, можно предположить, что магнитное поле независимо от природы тока его вызывающего возникает и вокруг одного заряда находящегося в движении.
Общее же поле в окружающей среде формируется из суммы полей создаваемых отдельными зарядами. Этот вывод можно сделать исходя из принципа суперпозиции. На основании различных опытов был получен закон, который определяет магнитную индукцию для точечного заряда. Это заряд свободно перемещается в среде с постоянной скоростью.
Формула 1 — закон электромагнитной индукции для движущегося точечного заряда
Где r радиус-вектор, идущий от заряда к точке наблюдения
Q заряд
V вектор скорости движения заряда
Формула 2 — модуль вектора индукции
Где альфа это угол между вектором скорости и радиус вектором
Эти формулы определяют магнитную индукцию для положительного заряда. Если ее необходимо рассчитать для отрицательного заряда то нужно подставить заряд со знаком минус. Скорость движения заряда определяется относительно точки наблюдения.
Чтобы обнаружить магнитное поле при перемещении заряда можно провести опыт. При этом заряд не обязательно должен двигаться под действием электрических сил. Первая часть опыта состоит в том, что по проводнику круговой формы проходит электрический ток. Следовательно, вокруг него образуется магнитное поле. Действие, которого можно наблюдать при отклонении магнитной стрелки находящейся рядом с витком.
Рисунок 1 — круговой виток с током воздействует на магнитную стрелку
На рисунке изображён виток с током, слева показана плоскость витка справа плоскость перпендикулярная ей.
Во второй части опыта мы возьмем сплошной металлический диск, закрепленный на оси от которой он изолирован. При этом диску сообщен электрический заряд, и он способен быстро вращаться вокруг своей оси. Над диском закреплена магнитная стрелка. Если раскрутить диск с зарядом, то можно обнаружить что стрелка вращается. Причем это движение стрелки будет таким же, как при движении тока по кольцу. Если при этом изменить заряд диска или направление вращения, то и стрелка будет отклоняться в другую сторону.
Рисунок 2 — вращающийся проводящий заряженный диск
Из этих опытов можно сделать вывод, что независимо от природы возникновения электрического тока. А также от носителей зарядов, которые его обеспечивают. Магнитное поле возникает вокруг всех движущихся зарядов.
5. Электрический ток — это упорядоченно движущиеся наряженные частицы. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Найдем силу, действующую на одну частицу.
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной 
, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Рассмотрим отрезок тонкого прямого проводника с током (рис. 1.23). Пусть длина отрезка и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля 
можно считать одинаковым в пределах этого отрезка проводника. Сила тока l в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения 
следующей формулой:
Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:
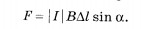
Подставляя в эту формулу выражение (1.4) для силы тока, получаем:
где N = nS — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
где 
— угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам и 
. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку распололсить так, чтобы составляющая магнитной индукции , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца Fл (рис. 1.24).
Электрическое поле действует на заряд q с силой 
. Следовательно, если есть и электрическое поле, и магнитное поле, то суммарная сила 
, действующая на заряд, равна:
= эл + л.
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии (см. учебник физики для 10 класса) это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Движение заряженной частици в однородном магнитном поле. Рассмотрим движение частицы с зарядом q в однородном магнитном поле , направленном перпендикулярно к начальной скорости частицы (рис. 1.25).
Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Так как магнитное поле не меняет модуль скорости движущейся частицы, то остается неизменным и модуль силы Лоренца. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что частица равномерно движется по окружности радиусом r. Определим этот радиус.
Использование действия магнитного поля на движущийся заряд. Действие магнитного поля на движущийся заряд широко используют в современной технике. Достаточно упомянуть телевизионные трубки (кинескопы), в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.
Сила Лоренца используется и ускорителе заряженных частиц (циклотрон) для получения частиц с большими энергиями. Циклотрон состоит из двух полых полуцилиндров (дуантов) 3, находящихся в однородном магнитном поле (рис. 1.26). Между дуантами создается переменное электрическое поле. Согласно формуле (1.6) при увеличении скорости частицы / радиус окружности (траектории 2), по которой движется частица, увеличивается. Период обращения частицы не зависит от скорости (см. формулу (1.7)), и, следовательно, через полпериода, вследствие изменения направления электрического поля, частица снова оказывается в ускоряющем ее поле и т. д. На последнем витке частица вылетает из циклотрона.
На действии магнитного поля основано также и устройство приборов, позволяющих разделять заряженные частицы по их уденьиым зарядам, т. е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц. Такие приборы получили название масс-электрографов.
На рисунке 1.27 изображена принципиальная схема простейшего масс-электрографа. Вакуумная камера прибора помещена в магинитое поле (вектор индукции перпендикулярен рисунку). Ускорение электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с высокой точностью измерить радиус траектории r. По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислить его массу.
На движущуюся заряженную часчицу со стороны магнитного поля действует сила Лоренца. Эта сила перпендикулярна скорости и не совершает работы.
ЭФФЕКТ ХОЛЛА
Эффект состоит в возникновении на боковых гранях проводника с током, помещенного в поперечное магнитное поле, разности потенциалов, пропорциональной величине тока I и индукции магнитного поля В.
Рассмотрим эффект, обусловленный действием лоренцевой силы 
на свободные заряды в проводнике. Представим себе проводник с током I в виде плоской ленты, расположенной в магнитном поле с индукцией 
, направленной от нас (рис. 2.19).
В случае изображенном на рис. 2.19, а, верхняя часть проводника будет заряжаться отрицательно, в случае 2.19, б – положительно.
аб
Рис. 2.19
Это позволяет экспериментально определить знак носителя заряда в проводнике.
При равной концентрации носителей заряда обоих знаков возникает холловская разность потенциалов, если различна подвижность, т.е. дрейфовая скорость носителей заряда.
Подсчитаем величину холловской разности потенциалов (Uх).
Обозначим: Ex – напряженность электрического поля, обусловленного ЭДС Холла, h – толщина ленты проводника.
 ,
| (2.10.1) |
Перераспределение зарядов прекратится, когда сила qEx уравновесит лоренцеву силу, т.е.
или 
Плотность тока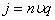 
,отсюда 
. Тогда 
.
Подставим Ex в (2.10.1) и найдем Ux:
 ,
| (2.10.2) |
где 
– коэффициент Холла.
Исследования ЭДС Холла привели к удивительным выводам. Металлы могут обладать проводимостью р -типа (Zn, Cd – у них дырки более подвижные, чем электроны). Это металлы с чуть перекрывающимися знаками, т.е. полуметаллы.
Из формулы (2.10.2) можно найти число носителей заряда:
 ,
| (2.10.3) |
Итак, измерение холловской разности потенциалов позволяет определить:
· знак заряда и тип носителей;
· количество носителей.
