Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО).
Основной закон динамики для неинерциальных систем отсчета: 
, где
— сила, действующая на тело со стороны других тел;
— сила инерции, действующая на тело относительно поступательно движущейся НСО. 
— ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;
— центробежная сила инерции, действующая на тело относительно вращающейся НСО. 
— угловая скорость НСО относительно ИСО, 
— расстояние от тела до центра вращения;
— сила инерции, действующая на тело, движущееся со скоростью 
относительно вращающейся НСО.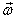 
— угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
Принцип Даламбера.
Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.
Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой 
. Под действием приложенных к ней внешних и внутренних сил 
и 
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение 
.
Введем в рассмотрение величину
,
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки (иногда даламберовой силой инерции).
Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам и прибавить силу инерции 
, то полученная система сил будет уравновешенной, т.е. будет
.
Метод Кинетостатики.
Важнейшим из принципов механики является принцип Даламбера. С принципом Даламбера тесно связан метод кинетостатики — способ решения задач динамики, в котором динамические уравнения записываются в форме уравнений равновесия. Метод кинетостатики широко применяется в таких общеинженерных дисциплинах, как сопротивление материалов, теория механизмов и машин, в других областях прикладной механики. Принцип Даламбера результативно используется и внутри самой теоретической механики, где с его
помощью созданы эффективные способы решения задач динамики.
