ВОПРОС 2
Точка,прямая.
Точка. как математическое понятие не имеет размеров. Очевидно, если объект проецирования является нульмерным образом, то говорить о его проецировании бессмысленно.
В геометрии под точкой целесообразно понимать физический объект, имеющий линейные измерения. Условно за точку будем принимать шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.
Прямая на комплексном чертеже может быть задана проекциями прямой; проекциями двух точек, принадлежащих прямой; проекциями отрезка прямой.
Метод Монжа
Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод - метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей

Рисунок 1.1 Точка в системе трех плоскостей проекций
Модель трех плоскостей проекций показана на рисунке 1.1. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x, y и z (абсцисса, ордината и аппликата).
Изображение точки общего и частного положения на эпюре
Для отрезка прямой характерны его размер и положение. То и другое определяется координатами концов отрезка. Положение отрезка характеризуется также углами его наклона к плоскостям проекций.
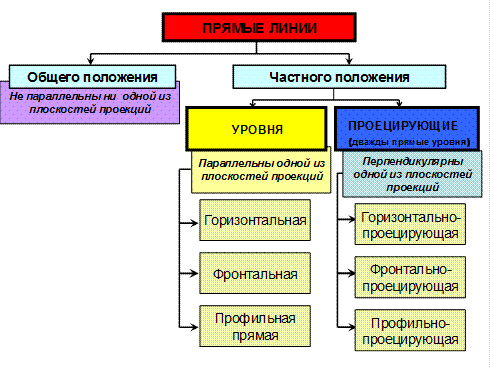
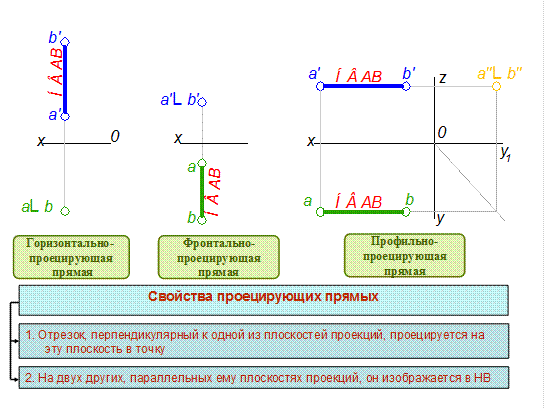
Прямые линии могут занимать в пространстве следующие положения относительно плоскостей проекций (рис. 2.1):
1. Прямые, не параллельные ни одной из плоскостей проекций, называются прямыми о б щ е г о п о л о ж е н и я.
2. Прямые, параллельные или перпендикулярные по отношению к плоскостям проекций, называются прямыми частного положения.