Алгоритм Макнотона
Рассмотрим систему с n идентичными процессорами, на которой необходимо решить L независимых задач; каждая задача решается одним процессором в течение времени
t i, i = 1,..., L. Требуется найти алгоритм, который для каждого данного пакета (набора) строил бы расписание решения задач на процессорах системы, обеспечивающее минимально возможное время решения. При этом достигается максимально возможная производительность системы. Например, в случае 2-процессорной системы и набора задач с временами (3,3,2,2,2) возможны различные варианты назначения задач на решение. Приведем некоторые из них (рис.3.35).
a)
б)
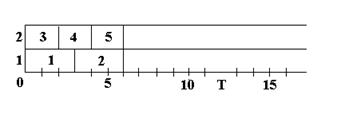T = T0 = θ
с)
Рис. 3.35. Варианты расписаний
Очевидно, что наилучший в смысле минимизации общего времени решения задач - вариант c), для которого время Т решения пакета задач совпадает с соответствующим оптимальным значением Т0и в данном случае равно величине
q = max { max ti, 1/n *å ti }
Величина q является нижней границей для оптимального значения Т0. Действительно, длина Т любого расписания не может быть меньше ни max t i - максимального из времен решения задач пакета П, ни величины (1/n *å ti), дающей длину расписания в том случае, когда до момента завершения решения последней из задач пакета ни один процессор не простаивает, т.е. все процессоры имеют 100% загруженности.
В общем случае даже при n = 2 задача поиска оптимального значения Т при условии решения задач, является NP-трудной, т.е. все известные алгоритмы ее решения имеют трудоемкость, экспоненциально зависящую от L. Однако, если допустить возможность прерывания решения задач пакета до завершения их обслуживания, то могут быть предложены полиномиально-трудоемкие алгоритмы, приводящие к расписанию оптимальной длины Т 0. При этом считается, что после прерывания решение задачи может быть возобновлено с точки прерывания на любом процессоре, не обязательно на том, на котором она первоначально решалась. Число прерываний должно быть по возможности меньшим, так как с каждым актом прерывания связаны потери машинного времени на загрузку-выгрузку задач из оперативной памяти.
Рассмотрим предложенный Макнотоном в 1959 г. алгоритм построения оптимального по длине расписания с не более чем n-1 прерываниями.
Алгоритм Макнотона заключается в предварительном упорядочении задач по убыванию времени решения и назначении задач последовательно по порядку номеров одну за другой на процессоры системы справа налево от уровня q.
Пример
n=2,L=4, времена решения задач:(5,4,3,2). Тогда
q = max {5, 1/2 *(5+4+3+2) } =7.
И расписание, полученное в соответствии с алгоритмом Макнотона, имеет следующий вид (рис. 3.36):
Рис. 3.36. Полученное расписание
В данном случае число прерываний равно единице.
Покажем, что n-1 (максимальное число прерываний для расписания, полученного в соответствии с алгоритмом Макнотона) является достижимой границей числа прерываний.
Для доказательства этого построим такой пример пакета задач, для которого алгоритм Макнотона дает расписание с числом прерываний n-1.
Пусть L=n+1 и t i = n, i= 1, n+1.
Тогда q = max { n, 1/n * (n+1)*n = n+1, а расписание, получаемое в соответствии с алгоритмом Макнотона, имеет вид (рис. 3.37):
Рис. 3.37. Расписание для n - процессорной системы по Макнотону
T=n+1=q
Число прерываний в этом случае, как видно, равно n-1,что и требовалось показать. Покажем теперь, что любое оптимальное расписание для этого пакета задач также имеет не менее n-1 прерываний. Очевидно, что в любом оптимальном расписании ни один процессор не простаивает на интервале [0,n+1]. Предположим, что существует некоторое оптимальное расписание с числом прерываний, меньшим n-1. Тогда по крайней мере 2 процессора (предположим для определенности P k и P l) обслуживают заявки без прерываний. Очевидно эти процессоры обслуживают некоторые задачи Z ik и Z il в интервале [0,n] без прерываний (если решение этих задач начинается позже момента времени t=0, значит до этого момента на этих процессорах решались некоторые другие задачи, решение которых прерывается в моменты начала решения задач Z ik и Z il). Найдутся моменты времени t, t`, такие, что n £ t < t` £ n+1, и в интервале [ t, t` ] хотя бы один процессор простаивает, а потому рассматриваемое решение не может быть оптимальным.
Так как мы пришли к противоречию, делаем вывод о том, что предположение о числе прерываний, меньшем n-1, в оптимальном расписании ложно.
