В материале раздела 3.6 использованы литературные источники [18], [27], [28], [37], [38], [39].
Параллельная обработка
Необходимость параллельной обработки может возникнуть по следующим причинам [27]:
1. Надо уменьшить время решения данной задачи.
2. Увеличить пропускную способность.
3. Улучшить использование системы.
Для распараллеливания необходимо соответствующим образом организовать вычисления. Сюда входит следующее:
· составление параллельных программ, т.е. отображение в явной форме параллельной обработки с помощью надлежащих конструкций языка, ориентированного на параллельные вычисления;
· автоматическое обнаружение параллелизма. Последовательная программа может быть автоматически проанализирована и выявлена явная или скрытая параллельная обработка. Последняя должна быть преобразована в явную.
Например.
Рассмотрим граф, описывающий последовательность процессов большой программы (см. рис.3.17).

Рис. 3.17. Граф выполнения большой программы
Из рисунка видно, что выполнение процесса р5 не может начаться до завершения процессов р2 и р3 и в свою очередь выполнение процессов р2 и р3 не может начаться до завершения процесса р1.
В данном случае для выполнения программы достаточно трех процессоров.
Ускорение обработки на многопроцессорной системе определяется отношением времени однопроцессорной обработки к времени многопроцессорной обработки, т.е.
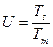 (4.1)
(4.1)
При автоматическом обнаружении параллельных вычислений мы различаем в последовательной программе явную и скрытую параллельную обработку. Хотя в обоих случаях требуется анализ программы, различие между этими видами обработки состоит в том, что скрытая параллельная обработка требует некоторой процедуры преобразования последовательной программы, чтобы сделать возможным ее параллельное выполнение. При анализе программы строится граф потока данных. Чтобы обнаружить явную параллельность процессов, анализируются множества входных (считываемых) переменных R (Read) и выходных (записываемых) переменных W (Write) каждого процесса. Два процесса i, j (i<>j) могут выполняться параллельно при следующих условиях:
Ri I Wj = Æ (пустое множество)
Wi I Rj = Æ
Wi I Wj = Æ
(4.2)
Это означает, что входные данные одного процесса не должны модифицироваться другим процессом и никакие два процесса не должны модифицировать общие переменные. Явная параллельная обработка может быть обнаружена среди процессов, удовлетворяющих этим условиям. Для использования скрытой параллельной обработки требуются преобразования программных конструкций, таких как:
· уменьшение высоты деревьев арифметических выражений;
· преобразование линейных рекуррентных соотношений;
· замена операторов;
· преобразование блоков IF и DO к каноническому виду;
· распределение циклов.
Проиллюстрируем эти преобразования на простых примерах. На
рис. 3.18 показаны деревья разбора для арифметического выражения (((a+b)+c)+d). На рис. 3.18а изображено дерево минимальной высоты (3) для первоначального выражения, а на рис. 3.18б - дерево, высота которого уменьшена до 2 путем преобразования первоначального выражения к виду (a+b)+(c+d) с использованием ассоциативности. Для арифметического выражения с n переменными или константами уменьшение высоты дерева позволяет достигнуть ускорения обработки порядка O(n/log2 n) при использовании O(n) процессоров. В примере, показанном на рис. 3.18, выражение может быть вычислено за два шага вместо трех первоначальных.
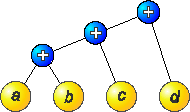
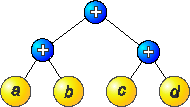
а) б)
Рис. 3.18. Деревья разбора до (а) и после (б) преобразования
Рассмотрим следующий блок операторов присваивания:
X=BCD+E
Y=AX
Z=X+FG
При использовании одного процессора этот блок может быть вычислен за 6 шагов, если один временный шаг отводится для каждой арифметической операции. Путем замены операторов можно получить следующий блок:
X=BCD+E
Y=ABCD+AE
Z=BCD+E+FG
Этот блок может быть вычислен параллельно за три шага с ускорением обработки 6/3 = 2 при использовании 5 процессоров.
Приведенные примеры преобразований показывают, какое ускорение можно получить, используя параллельную обработку и оптимизацию выражений.
Конвейерная обработка
Конвейерная обработка улучшает использование аппаратных ресурсов для заданного набора процессов, каждый из которых применяет эти ресурсы заранее предусмотренным способом. Хорошим примером конвейерной организации является сборочный транспортер на производстве, на котором изделие последовательно проходит все стадии вплоть до готового продукта. Преимущество этого способа состоит в том, что каждое изделие вдоль своего пути использует одни и те же ресурсы и как только некоторый ресурс освобождается данным изделием, он сразу же может быть использован следующим изделием, не ожидая, пока предыдущее изделие достигнет конца сборочной линии. Если транспортер несет аналогичные, но не тождественные изделия, то это – последовательный конвейер; если же все изделия одинаковы, то это – векторный конвейер.
Последовательные конвейеры. На рис. 3.19а показано устройство обработки команд, в котором имеется 4 ступени:
1. выборка команд из памяти;
2. декодирование;
3. определение адреса и выборка операнда;
4. исполнение.

а)
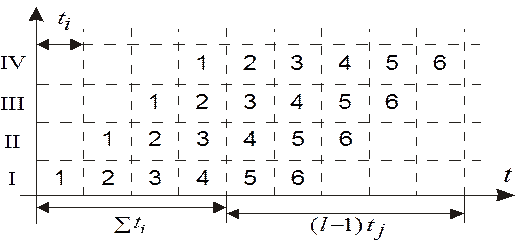
б)
Рис. 3.19. Четырехступенное устройство обработки команд
Ускорение обработки в данном устройстве измеряется отношением времени Ts, необходимого для последовательного выполнения L заданий (т.е. выполнения L циклов на одной обрабатывающей ступени), ко времени Tp выполнения той же обработки на конвейере. Обозначим через ti время обработки на i-той ступени, а через tj - соответствующее время для самой медленной ступени (см. рис.3.19б). Тогда если L заданий (команд) проходят через конвейер с n ступенями, то эффективность конвейера определяется следующим выражением,
для 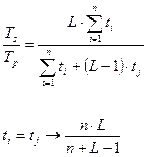 (4.3)
(4.3)
Векторные конвейеры. В них создается множество функциональных элементов, каждый из которых выполняет определенную операцию с парой операндов, принадлежащих двум разным векторам.
Эти пары подаются на функциональное устройство и со всеми элементами пар векторов функциональные преобразования проводят одновременно. Для предварительной подготовки преобразуемых векторов используются векторные регистры, на которые собираются подлежащие обработке вектора.
Типичное использование векторного конвейера – это процесс, вырабатывающий по двум исходным векторам А и В результирующий вектор С для арифметической операции СßА+В. В этом случае на конвейер поступает множество одинаковых команд.






