Методы корреляционного и регрессионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. Между тем в статистике приходиться сталкиваться с задачами измерения связи между качественными признаками. Такие методы измерения связи называются непараметрические.
Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла или коэффициент контингенции К. Пирсона. Расчетная таблица в этом случае состоит из четырех ячеек (таблица «четырех полей») и имеет следующий вид:
| Признаки | А (да) | 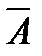 (нет) (нет)
| Итого |
| B (да) | a | b | а + b |
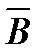 (нет) (нет)
| c | d | c + d |
| Итого | a + c | b + d | n |
Коэффициент ассоциации вычисляется по формуле:
 .
.
Коэффициент контингенции:
 .
.
Если по каждому из взаимосвязанных признаков выделяется число групп более двух то для подобного таблиц теснота связи между качественными признаками может быть измерена с помощью коэффициентов взаимной сопряженности К. Пирсона и А. А. Чупрова.
Коэффициент взаимной сопряженности Пирсона вычисляется по формуле:
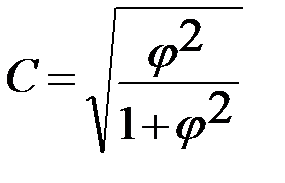 , где j2 – показатель средней квадратической сопряженности, который вычисляется по формуле:
, где j2 – показатель средней квадратической сопряженности, который вычисляется по формуле:
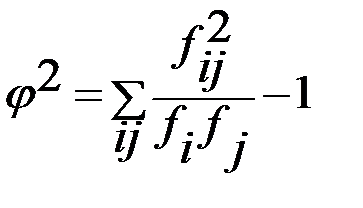 , где
, где  ,
,  .
.
Коэффициент Чупрова:
 , где К1, К2 – число групп по каждому из признаков.
, где К1, К2 – число групп по каждому из признаков.
Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что значение этих признаков могут быть проранжированы по степени убывания или возрастания, используется коэффициент корреляции рангов Спирмена:
 ,
,
где d – разность рангов признаков x и y;
n - число наблюдаемых единиц.
В случае отсутствия связи r = 0. При прямой связи коэффициент r - положительная правильная дробь, при обратной – отрицательная.
Если объём исходной информации небольшой, то необходимо выполнить проверку существенности рангового коэффициента, т. е. сверить с таблицей предельных значений. Расчетное значение r должно быть больше предельного.
Для определения тесноты связи между произвольным числом ранжированных признаков применяется коэффициент конкордации:
 ,
,
где m – количество факторов;
n - число наблюдений;
S - отклонение суммы квадратов рангов от средней квадратов рангов.
Рассмотрим пример:
В результате обследования студентов факультета получены следующие данные:
| Успеваемость | Количество студентов | Всего | |
| Посещающих спортивные секции | Не посещающих спортивные секции | ||
| Удовлетворительная | |||
| Неудовлетворительная | |||
| Итого |
Определите коэффициент ассоциации и контингенции между успеваемостью и посещаемостью спортивных секций.
Коэффициент ассоциации:
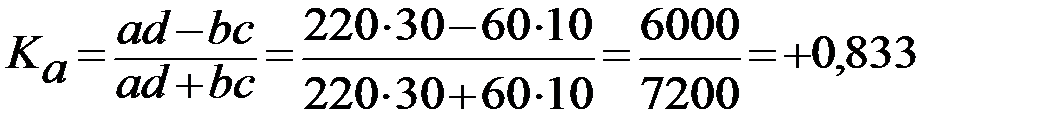
Коэффициент контингенции:
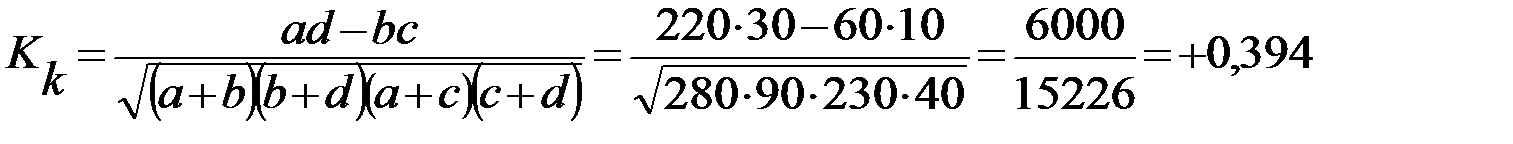 .
.
Полученные коэффициенты подтверждают наличие существенной связи между исследуемыми признаками. Однако коэффициент контингенции всегда меньше коэффициента ассоциации и дает более корректную оценку тесноту связи.






