Для изучения функциональных связей применяются балансовый и индексный методы.
Для исследования стохастических связей широко используется метод сопоставления параллельных рядов, метод аналитических группировок, корреляционный анализ, регрессионный анализ и некоторые непараметрические методы.
Установить наличие стохастической связи, а также получить представление о её характере и направлении можно с помощью сопоставления двух параллельных рядов статистических величин. Для этого факторы, характеризующие результативный признак, располагают в возрастающем или убывающем порядке (в зависимости от эволюции процесса или целей исследования), а затем прослеживают изменение результативного признака.
Стохастическая связь будет проявляться отчетливее, если применить для её изучения аналитические группировки. Чтобы выявить зависимость с помощью этого метода, нужно произвести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее или относительное значение результативного признака. Сопоставляя затем изменения результативного признака по мере изменения факторного, можно выявить направление, характер и тесноту связи между ними.
Рассмотрим основные проблемы статистического моделирования методами корреляционного и регрессионного анализа.
Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа – выбор типа модели (формы связи), установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной (функции регрессии).
Наиболее разработанной в теории статистики является методология т. н. парной корреляции, рассматривающая влияние вариации факторного признака x на результативный признак y и представляющая собой однофакторный корреляционный и регрессионный анализ.
Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. В большинстве случаев применяют линейную форму.
Уравнение однофакторной (парной) линейной корреляционной связи имеет вид:
,
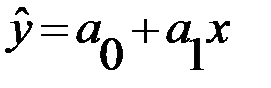где 
- теоретические значения результативного признака, полученные по уравнению регрессии; a0, a1 - коэффициенты (параметры) уравнения регрессии.
Уравнение показывает среднее значение изменения результативного признака y при изменении факторного признака x на одну единицу его измерения, т. е. вариацию y, приходящуюся на единицу вариации x. Знак a1 указывает направления этого изменения.
Параметры уравнения a0, a1 находят методом наименьших квадратов, т. е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi от выравненных 
:
.
Для нахождения минимума функции прировняем к нулю её частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
Решим эту систему в общем виде:
; 
.
Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:
, или 
.
Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным. При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерные для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин.
Явления общественной жизни складываются под воздействием не одного, а целого ряда факторов, т. е. эти явления многофакторны. Многофакторный корреляционный и регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель (уравнение) факторов при фиксированном положении (на среднем уровне) остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя.
Математически задача формулируется следующим образом:
.
Для расчета параметров простейшего уравнения множественной линейной двухфакторной регрессии: 
, где 
- расчетные значения зависимой переменной (результативного признака); 
- независимые переменные (факторные признаки); 
- параметры уравнения.
Строиться система нормальных уравнений:
Параметры этой системы могут быть найдены, например, методом К. Гаусса.
В случае линейной трехфакторной связи уравнение регрессии имеет вид:
.
Для расчета параметров по способу наименьших квадратов используют следующую систему нормальных уравнений:
Чтобы получить эту систему необходимо иметь таблицу следующих показателей: 
.
Для решения множественной регрессии с n – факторами 
система нормальных уравнений такова:
Многофакторный корреляционный и регрессионный анализ может быть использован в экономико-статистических исследованиях:
- для приближенной оценки фактического и заданного уровней;
- в качестве укрупненного норматива;
- для выявления резервов производства;
- для проведения межзаводского сравнительного анализа и выявления на его основе скрытых возможностей предприятий;
- для краткосрочного прогнозирования развития производства и пр.
Показатели тесноты связи.
Теснота корреляционной связи может быть измерена эмпирическим корреляционным отношением hэ, когда d2 (межгрупповая дисперсия) характеризует отклонение групповых средних результативного признака от общей средней: 
.
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отличать от эмпирического корреляционного отношения – теоретическое.
Теоретическое корреляционное отношение h представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выравненных значений результативного признака d, т. е. рассчитанных по уравнению регрессии, со средним квадратическим отношением эмпирических (фактических) значений результативного признака s:
h = 
,
где d2 = 
; s = 
Тогда h = 
.
Изменение значения h объясняется влиянием факторного признака.
В основе расчета корреляционного отношения лежит правило сложения дисперсий 
, где 
- отражает вариацию y за счет всех остальных факторов, кроме x, т. е. является остаточной дисперсией:
.
Тогда формула теоретического корреляционного отношения примет вид:
или 
.
Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации.
Корреляционное отношение может находиться в пределах от 0 до 1, т. е.
(0 £ h £ 1) Чем ближе корреляционное отношение к 1, тем связь между признаками теснее.
Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком.
Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи – линейный коэффициент корреляции:
где n – число наблюдений.
Для практических вычислений при малом числе наблюдений (n £ 20-30) линейный коэффициент корреляции удобнее исчислять по следующей формуле:
Он принимает значение в интервале: -1 £ r £ 1. Отрицательные значения указывают на обратную связь, положительные - на прямую. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при r = ± 1 связь – функциональная.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативными и несколькими факторными признаками, а также между каждой парой факторных признаков.
Множественный коэффициент корреляции вычисляется по формуле:
, где 
- дисперсия теоретических значений результативного признака, рассчитанная по уравнению множественной регрессии; 
- общая дисперсия результативного признака.
В случае оценки тесноты связи между результативным и двумя факторными признаками множественный коэффициент корреляции можно определить по формуле:
,
где r – парные коэффициенты корреляции между признаками., которые могут быть рассчитаны по следующим формулам:
;
;
.
