Цель работы: С помощью измерений поверхностного натяжения как функции концентрации проверить предположение о мономолекулярной адсорбции н-бутанола из водного раствора, определить величину предельной адсорбции G ¥и геометрические параметры мономолекулярного адсорбционного слоя.
Краткое теоретическое введение
Адсорбцией называется изменение концентраций компонент гетерогенной системы в поверхностном слое у границы контактирующих фаз по сравнению с концентрациями в объёме фаз. Обогащение поверхностного слоя данным компонентом (положительный избыток) называется положительной адсорбцией или просто адсорбцией, тогда как обеднение (отрицательный избыток) – отрицательной адсорбцией.
В качестве поверхностного слоя в системах жидкость/газ и жидкость/жидкость рассматривается узкая область пространства между контактирующими фазами, в пределах которой происходит непрерывное изменение свойств. Объёмные фазы (например a и b) являются однородными по составу и свойствам, но поверхность раздела между ними должна быть размыта на молекулярном уровне, то есть на расстояниях порядка 1 нм, из-за теплового движения молекул в каждой из фаз, и из-за постоянного обмена компонентами между фазами. Например, можно ожидать, что плотность вещества меняется приблизительно так, как показано на рис. 3.1. В связи с этим поверхностный слой следует рассматривать как отдельную фазу. Однако из-за неоднородности свойств и неопределённости толщины этого слоя в термодинамике принята математическая модель, согласно которой контактирующие фазы являются однородными вплоть до некоторой геометрической поверхности, где свойства фаз меняются скачком. На рис. 3.1 эта поверхность (перпендикулярная плоскости чертежа) показана пунктирной линией А–А'. В такой модели сумма объёмов фаз a и b равна общему объёму системы
, (3.1)
но суммы других экстенсивных параметров, взятые по контактирующим фазам, отличаются от соответствующих параметров системы на величины, которые относятся к двумерной (то есть, не имеющей толщины) поверхностной фазе, и которые называются поверхностными избытками. Например, если обозначить число молей i-ого компонента n i, то общее число молей этого компонента в системе составляет
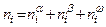, (3.2)
где верхние индексы a и b указывают принадлежность к соответствующим объёмным фазам, а индекс w означает принадлежность к двумерной поверхности раздела фаз. Величина
(3.3)
называется поверхностным избытком i-ого компонента, причем этот избыток (положительный или отрицательный) является следствием адсорбции.
Количественной характеристикой адсорбции i-ого компонента является величина G i(греческая прописная буква "гамма"), которая определяется как отношение поверхностного избытка этого компонента к площади S поверхности раздела фаз:
. (3.4)
Основной единицей измерения этой величины является моль/м2. Согласно рекомендациям IUPAC её следует называть избыточной поверхностной концентрацией компонента i. Однако на практике её часто называют просто адсорбцией, адсорбцией Гиббса или иначе.
Как было показано первоначально Гиббсом, и позднее подтверждено другими теоретическими и экспериментальными исследованиями, межфазное (поверхностное) натяжение раствора s связано с величинами адсорбции Г iуравнением
, (3.5)
где m i– химический потенциал i-ого компонента раствора. В частности, для бинарного раствора (двухкомпонентная система) это уравнение имеет вид
. (3.5а)
Благодаря тому, что положение поверхности раздела фаз (А–А' на рис. 3.1) является произвольным в пределах поверхностного слоя, адсорбция Г iодного из компонент всегда может быть принята равной нулю. Обычно, нулевой принимают адсорбцию того компонента, который в растворе находится в избытке, то есть растворителя. При таком выборе уравнение (3.5а) для бинарного раствора имеет решение
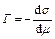, (3.6)
где Г и m - адсорбция и химический потенциал, соответственно, растворённого вещества. Химический потенциал связан с концентрацией С по уравнению m = m 0 + RT ln(g C), где g - коэффициент активности, m 0 – химический потенциал растворённого вещества при активности g C равной 1. Подстановка этого выражения в уравнение (3.6) и дифференцирование при Т = const приводит к уравнению
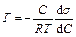, (3.6а)
в котором коэффициент активности g опущен.
Уравнение (3.6а) носит название уравнения Гиббса и является фундаментальными в теории адсорбции. Оно показывает, что если растворённое вещество снижает поверхностное натяжение раствора по сравнению с поверхностным натяжением чистого растворителя, то оно адсорбируется положительно. Если растворённое вещество повышает поверхностное натяжение раствора, то оно адсорбируется отрицательно (то есть, поверхностный слой раствора обеднён этим веществом). Обратные утверждения равно справедливы: если растворённое вещество адсорбируется на поверхности раздела фаз, то s уменьшается, а если оно имеет отрицательную адсорбцию, то s увеличивается.
В системе водный раствор/воздух различные растворимые вещества показывают три основные типа зависимости s от С. Низкомолекулярные сильные электролиты (органические и неорганические соли, кислоты и основания) показывают приблизительно линейное увеличение s с увеличением концентрации (рис. 3.2а). Согласно уравнению 3.5а, это соответствует отрицательной адсорбции во всём диапазоне концентраций. Одна из причин этого поведения состоит в том, что ионы имеют высокую теплоту гидратации. Адсорбция на поверхности вода/воздух требует частичной или полной дегидратации, что является термодинамически невыгодным. Поэтому поверхностный слой обеднён растворённым электролитом. Низкомолекулярные органические неэлектролиты, содержащие в своей структуре как неполярные связи типа С–С и С–Н так и полярные связи типа О–Н, N–H и С=О (спирты, альдегиды, кетоны, амины и аналогичные вещества), показывают постепенное уменьшение s с увеличением концентрации (рис. 3.2б). Наконец, существует группа растворимых в воде органических веществ, молекулы которых содержат протяжённые после-довательности неполярных ковалентных связей типа С–С наряду с ионными или высокополярными связями. Эти вещества обнаруживают сильное уменьшение s в области низких концентраций, и почти полное отсутствие зависимости s от концентрации в области высоких концентраций (рис. 3.2в).
Первая группа веществ представляет ограниченный практический интерес и, поэтому, редко является предметом исследований. Вторая и третья группы являются важными и имеют специальное название – поверхностно-активные вещества (сокращённо ПАВ), причём третья группа веществ называется амфифильными ПАВ. В количественном отношении, способность ПАВ понижать поверхностное натяжение характеризуется величиной -d s /d C, которую называют поверхностной активностью. В гомологических сериях ПАВ, например в серии спиртов Н3С(СН2)nOH, поверхностная активность увеличивается с увеличением длины углеводородной цепи. Согласно эмпирическому правилу Траубе, при комнатной температуре в системе водный раствор/воздух величина -d s /d C увеличивается приблизительно в 3.2 раза при увеличении длины углеводородной цепи на одну группу СН2.
Амфифильные ПАВ, имеющие наиболее высокую поверхностную активность, подробно рассматриваются в лабораторной работе 5, тогда как настоящая работа посвящена адсорбции низкомолекулярных спиртов.
Алифатические одноатомные спирты имеют асимметричное химическое строение. На одном конце молекулы находится группа С–О–Н с относительно высоким дипольным моментом, тогда как остальная часть молекулы построена из неполярных связей С–С и С–Н. Вследствие этого, полярная часть имеет высокую энергию сольватации полярными растворителями, тогда как неполярная часть имеет низкую энергию сольватации. Поскольку воздух является неполярной средой, для водных растворов спиртов можно ожидать определённую ориентацию адсорбированных молекул в поверхностном слое водный раствор/воздух. Полярные группы атомов должны ориентироваться преимущественно в сторону фазы раствора, а неполярные группы атомов – в сторону фазы воздуха, как схематически показано на рис. 3.3. Можно ожидать далее, что степень упорядоченности такой ориентации зависит от энергии теплового вращательного движения молекулы: упорядоченность должна быть тем выше, чем ниже температура и чем больше молекулярная масса спирта (или, точнее, чем больше момент инерции молекулы). Фактически, при комнатной температуре чистый этиловый спирт имеет такое же поверхностное натяжение, какое имеют жидкие углеводороды, например н-октан. Это косвенно свидетельствует, что на поверхности раздела спирт/воздух все или большинство молекул спирта ориентированы метильными группами СН3 в сторону воздуха.
Из аналогичных соображений о полярности связей и энергии сольватации можно ожидать, что гидроксильные группы адсорбированных молекул окружены преимущественно молекулами более полярного компонента – воды, когда она (вода) присутствует в достаточной концентрации. С другой стороны, неполярные окончания этих молекул должны контактировать преимущественно с неполярными молекулами О2 и N2 воздуха. Из этого следует представление о мономолекулярной адсорбции, то есть о такой адсорбции из разбавленного раствора, при которой образуется адсорбционный слой толщиной в одну молекулу (рис. 3.4а), в противоположность полимолекулярной адсорбции (рис. 3.4б). При адсорбции на границе водный раствор/воздух полимолекулярная адсорбция могла бы наблюдаться для веществ с симметричным химическим строением молекул, например N2, СН4, С2Н6 и т.п., но такие вещества практически нерастворимы в воде.
Поскольку адсорбированная молекула занимает в адсорбционном слое некоторую площадь, число молекул, которое может адсорбироваться при мономолекулярной адсорбции, ограничено. Из этого следует, что при увеличении концентрации адсорбция Г должна стремиться к некоторому пределу, при котором вся поверхность раздела фаз занята молекулами спирта, то есть является насыщенной (рис. 3.4в). Этот предел принято называть предельной адсорбцией Г ¥.
Представление о мономолекулярном слое является сильным упрощением, поскольку, как обсуждалось выше, поверхностный слой на границе фаз должен быть размыт на расстояниях порядка 1 нм. Тем не менее, экспериментальные исследования адсорбции ПАВ из растворов в основном находятся в согласии с этим упрощением. В области низких концентраций ПАВ, адсорбция Г приблизительно следует уравнению Лэнгмюра
, (3.7)
выведенному теоретически для мономолекулярной адсорбции на поверхности с фиксированным числом адсорбционных центров на единице площади (см. лаб. работу 4). Из этого уравнения может быть найдена предельная адсорбция экстраполяцией зависимости
(3.7а)
к С –1 = 0 или к С = ¥. То есть, насыщенный мономолекулярный адсорбционный слой (рис. 3.4 в) является гипотетическим, так как предел С = ¥ отвечает нулевой концентрации воды, при которой этот слой не может быть мономолекулярным. Однако с помощью Г ¥можно найти характеристики реальных (ненасыщенных) мономолекулярных слоёв.
Поскольку адсорбция Г ¥представляет число молей вещества, приходящееся на единицу площади поверхности, её обратная величина равна площади, приходящейся на 1 моль вещества. Тогда площадь s о, занимаемая одной молекулой в мономолекулярном слое, составляет
, (3.8)
где NA – число Авогадро.
Предполагая, что гипотетический насыщенный слой является чистым адсорбатом (то есть, спиртом в данной работе), можно вычислить массу адсорбционного слоя, приходящуюся на единицу площади, как произведение Г ¥и молекулярной массы адсорбата М. Отношение массы к плотности r чистого адсорбата имеет смысл объёма адсорбционного слоя, но, поскольку этот объём относится к единице площади поверхности, данное отношение равно толщине d адсорбционного слоя:
(3.9)
Предположение об образовании мономолекулярного адсорбционного слоя можно проверить сопоставлением величин s о и d, найденных по уравнениям 3.8 и 3.9 из экспериментальных данных, с теоретическими оценками этих величин, сделанными из геометрических соображений. Наиболее просто оценить вероятную толщину мономолекулярного слоя. В насыщенном слое молекулы спирта должны располагаться строго вертикально, то есть перпендикулярно поверхности раздела фаз. При такой ориентации толщина слоя d должна быть равна длине молекулы. В первом приближении, молекулу первичного одноатомного спирта можно представить плоской моделью с линейной последовательностью связей углеводородной цепи Н–(СН2–)NС–О–Н (см. рис 3.5а). Как известно из структурных исследований разреженных паров и кристаллических спиртов, длины связей в среднем равны: 1.10 Å для С–Н, 1.54 Å для С–С, 1.43 Å для С–О и 0.91 Å для О–H. Тогда длина молекулы спирта, содержащего N углеводородных атомов углерода в неразветвленной цепи, составляет в этой модели
L ' [Å] = 1.10 + 1.54×N + 1.43 + 0.91 = 1.54×N + 3.44 (3.10)
Например, длина н-гептанола С7Н15ОН (выбранного в качестве примера на рис. 3.5а) в этом приближении составит 1.54×6 + 3.44 = 12.68 Å. Следовательно, можно ожидать для адсорбционного слоя этого спирта толщину d '» 1.3 нм.
В следующем приближении необходимо учесть, что в реальной молекуле валентные углы при атомах углерода и кислорода не могут быть равны 180° и 90°, как принято на рис. 3.5а, а должны быть равны приблизительно 109.47°, соответственно sp3 валентному состоянию этих атомов, причём валентные углы ССС должны лежать приблизительно в одной плоскости, образуя зигзагообразную конформацию (рис. 3.5 б). При такой конформации длину молекулы можно вычислить как сумму проекций длин связей на ось симметрии углеводородного радикала (СН2–)N:
L '' = {1.54×N + 3.44} sin(109.47/2) (3.10а)
Длина молекулы н-гептанола в этом приближении составит {1.54×6 + 3.44}×sin(109.47/2) = 10.35 Å и толщина мономолекулярного слоя d ''» 1.0 нм.
Труднее оценить площадь, занимаемую одной молекулой в насыщенном слое. Снова предполагая строго вертикальную ориентацию молекул, можно принять её равной квадрату расстояния между вертикальными осями соседних молекул. Это расстояние должно складываться из собственно "толщины" молекулы плюс расстояние межмолекулярного взаимодействия между соседними молекулами. При рассмотрении "толщины" необходимо учесть, что из-за малого момента инерции относительно вертикальной оси, молекулы должны совершать свободное вращение вокруг этой оси при температуре выше точки плавления спирта. Поэтому эффективная толщина должна быть равна диаметру окружности, которую описывают при вращении атомы, наиболее удалённые от вертикальной оси. Как поясняет рис. 3.5 в, этот диаметр равен двум расстояниям С–Н плюс горизонтальная проекция связи С–С, то есть 2×1.10 + 1.54×cos(109.47/2) = 3.09 Å. Ближайшее расстояние, на которое могут подходить соседние молекулы, определяется расстоянием ван-дер-ваальсового взаимодействия между атомами водорода СН2 групп этих молекул. В отличие от валентных связей, оно зависит как от природы молекул, так и температуры и давления. В кристаллических телах, ван-дер-ваальсово расстояние Н…Н составляет обычно от 2.0 до 3.0 Å. Принимая, что эти величины справедливы так же для адсорбционного монослоя, расстояние между вертикальными осями можно оценить в пределах от 3.09 + 2.0 = 5.09 Å до 3.09 + 3.0 = 6.09 Å. Тогда площадь s о составляет:
s о = от (5.09 Å)2 до (6.09 Å)2 или от 0.26 нм2 до 0.37 нм2 (3.11)
Эта оценка s o не зависит от длины углеводородной цепи спирта.
Фактически, из экспериментальных исследований адсорбции н-гептанола была найдена толщина адсорбционного слоя 1.01 нм и площадь s o 0.30 нм2 (при 25 °С), причем из исследований других спиртов известно, что s0 уменьшается приблизительно от 0.4 до 0.3 нм2 с увеличением длины углеводородного радикала. Этот последний факт объясняется усилением ван-дер-ваальсового притяжения между соседними молекулами спирта при увеличении длины молекулы.
Приборы и методы измерений
План исследования адсорбции из растворов при постоянной температуре включает следующие стадии:
- измерение s как функции концентрации в серии растворов ПАВ,
- нахождение адсорбции G как функции концентрации ПАВ путём дифференцирования полученной зависимости σ от концентрации,
- нахождение предельной адсорбции G ¥путём экстраполяции концентрационной зависимости G на основе уравнения Лэнгмюра,
- вычисление параметров мономолекулярного адсорбционного слоя из найденной величины G ¥.
Для измерения поверхностного натяжения на поверхности раздела жидкость/газ (в частности, жидкость/воздух) могут быть использованы различные способы. Наиболее распространёнными являются: 1) измерение максимального давления пузырьков газа; 2) измерение веса капель жидкости (сталагмометрический метод); 3) измерение капиллярного поднятия уровня жидкости; 4) метод отрыва кольца от поверхности жидкости (метод Дю Нуи).
В последнем методе, лёгкое проволочное кольцо (обычно из платиновой проволоки) со сравнительно большим радиусом R подвешивают горизонтально на пружинке из кварцевого стекла (так наз. кварцевые весы), измеряют вес кольца в воздухе, mg, затем осторожно опускают его на поверхность испытуемой жидкости так, чтобы оно свободно плавало, и измеряют силу F, необходимую для отрыва кольца от поверхности жидкости, с помощью того же динамометра. Сила F связана с поверхностным натяжением жидкости по уравнению
F = mg + 4p Rs
откуда следует s = (F – mg)/4p R.
В методе капиллярного поднятия жидкости, стеклянный капилляр, открытый с обоих концов, погружают одним концом в жидкость, и с помощью точного оптического инструмента (катетометра или горизонтального микроскопа) измеряют высоту H поднятия мениска жидкости в капилляре над уровнем жидкости вне капилляра (см. рис. 6.3). В этом методе особенно важным является достижение равновесной высоты мениска, которая зависит от достижения равновесия жидкость/пар над жидкостью внутри капилляра. Это равновесие устанавливается медленно. Равновесная высота Н связана с поверхностным натяжением жидкости по уравнению Жюрена
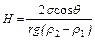
Из него может быть вычислено поверхностное натяжение s. В этом уравнении q - угол смачивания стенок капилляра жидкостью, r – радиус (внутренний) капилляра, r 2 и r 1 – соответственно плотность жидкости и плотность газа, вытесняемого жидкостью из капилляра. Метод широко применяется для жидкостей, хорошо смачивающих стекло, таких как вода и разбавленные водные растворы, поскольку в этом случае cos q приблизительно равен 1.
Сталагмометрический метод является одним из самых простых. Он основан на подсчёте числа капель n, за которое определённая масса жидкости, m, вытекает из капиллярной трубки с внешним радиусом R. Вес одной капли, mg/n, связан с поверхностным натяжением по уравнению: mg/n = 2p× Rs (уравнение Тейта). Этот метод обсуждается подробно в лабораторной работе 5.
В настоящей работе используется метод наибольшего давления в пузырьке. Согласно этому методу, капилляр, с внутренним радиусом r приблизительно 1 мм, погружают на небольшую глубину в жидкость, которая поддерживается при постоянном гидростатическом давлении и температуре. Жидкость находится в замкнутом сосуде, сообщающимся с вакуумным насосом и манометром, тогда как верхний конец капиллярной трубки сообщается с атмосферой. Давление над свободной поверхностью жидкости (то есть за пределами капилляра; см. рис. 3.6) постепенно понижают с помощью вакуумного насоса, в результате чего у нижнего кончика капилляра появляется пузырёк газа (воздуха). Когда пузырёк принимает форму полусферы, достигается равенство сил, действующих на него, и он отрывается от стеклянной трубки и всплывает. Сила, "выдувающая" пузырёк, равна произведению площади кругового сечения капилляра на перепад давления, p r 2(P 1 – P 2), тогда как сила, препятствующая образованию пузырька, равна "стягивающей" силе, то есть произведению длины окружности кругового сечения на поверхностное натяжение, 2p rs. Из равенства p r 2(P 1 – P 2) = 2p rs следует:
s = r (P 1 – P 2)/2 (3.12)
Максимальное давление в пузырьке (P 1 – P 2), при котором он отрывается, определяют по высоте h столба нелетучей жидкости, находящейся в манометре и обладающей плотностью r. Тогда
(P 1 – P 2) = hrg и s = rhrg /2 (3.13)
Если при исследовании серии разбавлений раствора ПАВ в одном и том же приборе принять, что поверхностное натяжение растворителя - воды известно и равно s о, то уравнение (3.13) можно представить в рабочем виде
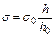(3.14)
где h о – высота столба жидкости в манометре при измерении максимального давления пузырька в воде (то есть при нулевой концентрации ПАВ). Зная поверхностное натяжение воды s о и измеряя экспериментально h и h о можно вычислять s для растворов ПАВ.
Последовательность выполнения работы
Готовят серию разбавлений раствора ПАВ. Например, при исследовании водных растворов н-бутанола могут быть использованы концентрации 0.3, 0.15, 0.075, 0.0375, и 0.0188 моль/л. Если работа проводится без термостата, необходимо предварительно измерить температуру основного раствора (из которого готовят разбавления) и дистиллированной воды. Различие должно быть менее 1 °С. Температуру растворов в любом случае следует записать. Измерения поверхностного натяжения начинают с чистой воды и продолжают в порядке увеличения концентрации ПАВ.
Перед началом измерений, устанавливают манометр 5 прибора (рис. 3.7) в такое наклонное положение, при котором мениск манометрической жидкости находится в нижней части шкалы. Если положение мениска не отвечает нулю шкалы прибора, то его фактическое положение следует записать как Н (рабочий нулевой уровень). Соединяют отводную трубку 3 с водоструйным насосом (на рис. 3.7 не показан) и манометром 5. Включают водопроводную воду водоструйного насоса до некоторого (небольшого) напора и наливают первый раствор (воду) в пробирку 1 в таком объёме, чтобы капиллярная трубка 2 погружалась в него приблизительно на 1 мм и уровень жидкости оставался ниже отводной трубки пробирки 1. Закрывают пробирку пробкой капиллярной трубки и осторожно ослабляют запорный микровинт 4 так чтобы через капилляр трубки 2 проскакивали пузырьки воздуха с постоянной скоростью один пузырёк за 5-10 секунд. В течение этого времени на поверхности очередного пузырька успевает установиться равновесие. При проскакивании пузырьков уровень рабочей жидкости на шкале манометра 5 колеблется от нижнего уровня Н до некоторого верхнего уровня h ', характерного для данного раствора. Этот уровень следует считать с шкалы прибора и разность h = h ' – Н записать как очередной результат измерения. После этого, микровинт 4 закрывают и повторяют измерение с тем же раствором – то есть, ослабляют микровинт до постоянной скорости проскакивания пузырьков, считывают показание манометра и закрывают микровинт. Рекомендуется проводить не менее пяти повторных измерений. Затем переходят к следующему раствору в порядке увеличения концентрации.
Необходимо подчеркнуть, что все измерения должны быть проведены при постоянном напоре водопроводной воды в водоструйном насосе; то есть, водопроводный вентиль должен оставаться в одном положении до окончания всех измерений. Важно так же, чтобы при заполнении пробирки 2 раствором он не попадал в отводную трубку этой пробирки и далее в вакуумную систему прибора. Присутствие жидкости в вакуумных трубках или колебания напора в водоструйном насосе могут быть причиной неправильных результатов.
Обработка и оформление результатов 
1. Результаты измерений уровня манометрической жидкости h заносят в таблицу (см. табл. 3.1) и вычисляют среднее значение, 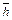, для каждой концентрации С. Поверхностное натяжение, s, вычисляют по формуле (3.14), причем поверхностное натяжение воды, s о , для фактической температуры измерений находят из табличных данных (приложение 4), при необходимости используя интерполяцию (см. инструкцию в приложении 4).
2. По данным в табл. 3.1 вычерчивают изотерму поверхностного натяжения, то есть зависимость s от С. Дифференцируют её графическим методом. Для этого строят касательные к полученной кривой для нескольких (не менее пяти) произвольных значений концентрации, и продолжают их до пересечения с осью s (как показано в качестве примера на рис. 3.8 для одной концентрации С = 0.1 моль/л). Наиболее точные результаты получаются при использовании прямоугольного зеркальца (приложение 2.2), однако даже в этом случае точность построения касательных становится слишком низкой при высокой концентрации. Поэтому для дифференцирования следует выбирать сравнительно невысокие концентрации, при которых s снижается не более чем на ~20 мН/м по сравнению с s о. Выбранные концентрации заносят в отдельную таблицу (см. табл. 3.2).
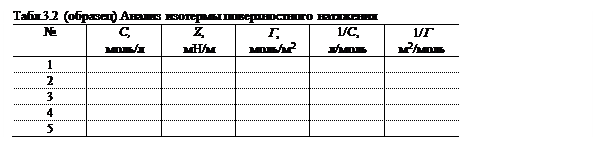
3. С помощью построенных касательных определяют адсорбцию Г. Входящая в уравнение Гиббса (3.6а) производная –d s /d C для каждой из выбранных концентраций равна коэффициенту наклона соответствующей касательной (отношение сторон треугольника СВ/ВА на рис. 3.8), а произведение – С d s /d C равно произведению этого коэффициента на данную концентрацию, то есть произведению (СВ/ВА)×ВА = СВ. Если отрезок СВ обозначить Z, уравнение Гиббса можно переписать в виде
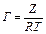(3.15)
Таким образом, для нахождения Г следует определить отрезки Z для каждой из касательных и вычислить Г по уравнению (3.15). Результаты занести в таблицу.
4. Из полученных данных находят предельную адсорбцию Г ¥, как параметр уравнения Лэнгмюра (3.7). Для этого уравнение Лэнгмюра следует представить в линейном виде (3.7а), из которого можно определить величину, обратную Г ¥, экстраполяцией зависимости Г –1 от С –1 к С –1 = 0 (то есть к С = ¥). Для этого следует вычислить обратные величины Г и С (в табл. 3.2) и использовать два метода: графический метод (см. рис. 3.9) и вычислительный метод наименьших квадратов (приложение П3.2).
5. С помощью найденного значения Г ¥вычислить площадь s0, занимаемую одной молекулой в адсорбционном слое, по уравнению (3.8), толщину адсорбционного слоя d по уравнению (3.9). Плотность н-бутилового спирта можно найти из интерполяционного уравнения для температур, близких к комнатной:
r (г/cм3) = 0.8239 – 0.699×10–3 T – 0.32×10–6 T 2 (3.16)
где Т – температура в °С.
6. Вычислить теоретическую толщину мономолекулярного слоя для н-бутанола по уравнению 3.10а, и сравнить результат вычисления с экспериментальным значением d, а также сравнить экспериментальное значение s о с теоретической оценкой s о по уравнению 3.11. Для объективного сравнения рекомендуется применить метод, описанный в приложении 3.3. Сделать вывод о согласии или несогласии результатов работы с гипотезой мономолекулярной адсорбции спиртов.
Контрольные вопросы
1. Что называется адсорбцией и что является количественной мерой адсорбции?
2. Что называется поверхностным натяжением раствора? В каких единицах измерения выражают численные значения s?
3. Как связана адсорбция из раствора с поверхностным натяжением раствора?
4. Какие вещества повышают и какие понижают поверхностное натяжение водных растворов? Как объяснить это различие с помощью адсорбции?
5. Что можно сказать о зависимости s от концентрации и о величинах адсорбции компонент в системе раствор воды в спирте/воздух? Каким компонентом обогащён поверхностный слой, уменьшается или увеличивается s с увеличением концентрации воды?
6. Как формулируется правило Траубе? Какой вывод можно сделать из него о зависимости избыточной поверхностной концентрации Г от строения молекулы ПАВ?
7. Что называется мономолекулярным адсорбционным слоем? Какие параметры используются для его характеристики?
8. В чём заключаются основные стадии лабораторной работы?
9. Какие методы применяются для измерения поверхностного натяжения?
10. В чем заключается метод наибольшего давления пузырька? Опишите принципиальное устройство прибора для измерения s этим методом.
Литература
Зимон А.Д., Балакирев А.А., Дехтяренко Н.Г., Бабак В.Г., Аксёнов В.Н. Коллоидная химия. Лабораторный практикум. Часть 1. М: ВЗИПП 1986, Лаб. работа 3.
Мелвин-Хьюз Э.А. Физическая химия. Том 2. (пер. с англ.) М: Издатинлит 1962, Глава 19.
Адамсон А. Физическая химия поверхностей. (пер. с англ.) М: Мир 1979, Главы 1 и 2.
Джейкок М, Парфит Г. Химия поверхностей раздела фаз. (пер. с англ.) М: Мир 1984, Главы 2 и 3.
IUPAC, Division of Physical Chemistry. Manual of symbols and terminology for physico-chemical quantities and units. Pure and Applied Chemistry 1972, vol. 31, 577-638 (дефиниции терминов и понятий в термодинамике адсорбции)
Nakagaki M., Yamamoto M. The theory of the adsorption monolayer with lateral intermolecular interactions and its application to aqueous alcohol solutions. Bulletin of the Chemical Society of Japan 1977, vol. 50, 873-878. (параметры мономолекулярных слоёв низкомолекулярных спиртов)
Posner A.M., Anderson J.R., Alexander A.E. The surface tension and surface potential of aqueous solutions of normal aliphatic alcohols. Journal of Colloid Science 1952, vol. 7, 623-640 (экспериментальные точки для рис. 3.8)
Landolt-Börnstein. Physikalisch-chemische Tabellen. Berlin etc: Springer-Verlag 1927-1976 (уравнение 3.16)
Рис. 3.1 Изменение свойства Y (например, плотности) в пространстве между контактирующими фазами a и b. Непрерывная линия показывает реальное изменение Y. Пунктирные линии показывают изменение Y в классической термодинамической модели, причем вертикальная линия А–А' отвечает произвольно выбранной математической поверхности раздела фаз.
Рис. 3.2 Типичные изотермы поверхностного натяжения водных растворов. (а) раствор хлорида натрия при 20 °С; (б) раствор этилового спирта при 25 °С; (в) раствор лаурилсульфата натрия (приблизительная кривая). При сравнении кривых следует обратить внимание на различие концентраций по осям абсцисс.
Рис. 3.3 Ориетация молекулы С2Н5ОН
Рис. 3.4 Иллюстрация понятий (а) мономолекулярная адсорбция, (б) полимолекулярная адсорбция, (в) предельная мономолякулярная адсорбция (насыщенный мономолекулярный слой).
Рис. 3.5 Последовательность химических связей в молекуле спирта (на примере н-гептанола) используемая для вычисления длины и "толщины" молекулы. а) Плоская модель с линейной последовательностью связей, б) модель, учитывающая валентные углы связей вдоль длины, в) элемент структуры, иллюстрирующий эффективную "толщину" молекулы в жидком состоянии
Рис. 3.6 Образование пузырька воздуха на конце капиллярной трубки, погруженной в жидкость.
Рис. 3.7 Экспериментальная установка для измерения наибольшего давления в пузырьках. 1 – пробирка с раствором ПАВ, 2- капиллярная трубка с пробкой, 3 – резиновая трубка, 4 – запорный микровинт, 5 – U-образный манометр
Рис. 3.8 Изотерма поверхностного натяжения водных растворов н-бутанола (Т = 12 °С). Показано графическое построение для одной произвольно выбранной концентрации, с помощью которого получают величину Z (отрезок СВ в единицах измерения оси ординат).
Рис. 3.9 Пример графической экстраполяции для нахождения обратной величины предельной адсорбции. (Точки на графике соответствуют кривой на рис. 3.8)
